模拟退火算法解决带容量约束的车辆路径优化问题

---

前言

带有约束的车辆路径问题( capacitated vehicle routing problem，CVRP) 是在标准车辆路径问题的基础上增加能力约束使模型更加符合现实生活中遇到的配送问题模型。CVRP 问题可以描述为：某配送中心用多辆相同汽车向有不同需求的客户配送货物，已知每个客户的位置、需求量以及汽车的容量，配送路径受车辆的容量、行驶路程等限制，需要合理安排车辆配送选择最佳车辆路径，使得总路程最短、总费用最小、配送总时间最短等。

---

一、提出假设

车辆路径问题( VRP) 一直都是 NP-hard 难题，对于这种多目标多约束的问题，其结果也是受到很多因素的影响，需要做出一定的假设，尽可能地减小不必要的因素对结果的影响，减少求解难度，使最终结果更加符合现实生活中的要求。
所做出的假设如下：
(1) 配送中心具有固定的车辆数且每辆车车型完全相同。
(2) 每辆车可以满足多个客户点的需求，而每个客户点只能被一辆车服务，在配送服务完成之后车辆要驶回车场。
(3) 假设车辆配送产生的成本与路径长度线性相关，每辆车固定成本相同。
(4) 每辆车载量有限，客户点的总需求量不得超过车队总装载量。
(5) 有且只有一个配送中心。

二、数学模型

1.CVRP优化模型

基于图论的表述方式，多目标优化VRP问题描述：在一个无向图G=(V, E)中，其中，V={0,1,…,n}为图中所有节点集合，0表示配送中心，V”={1,2,…,n}为顾客节点集合，E为任意两节点的边，E={(i,j)|i,j∈V,i≠j}表示边集，每条边的权重为cij(i,j∈V,i≠j)表示从顾客点i到顾客点j的配送运输距离。
设xijk定义如式（1）：
$$x_{ijk}=\{\begin{array}{ll}1,& \text{若车辆k访问顾客i后访问顾客j}\\ 0,& \text{否则}\end{array}\text{\hspace{1em}(1)}$$

则文本总结出的VRP的三个目标函数如式（2）
$$\begin{array}{rl}min{Z}_1& ={\sum }_{k\in v}{\sum }_{i\in c}{\sum }_{j\in c}{D}_{ij}{x}_{ijk}\\ min{Z}_2& ={\sum }_{k\in v}{\sum }_{j\in c}{x}_{ijk}\\ min{Z}_3& =ma{x}_k^v{\sum }_{i\in c}{\sum }_{j\in c}{D}_{ij}{x}_{ijk}\end{array}\text{\hspace{1em}(2)}$$
约束条件为
$$\sum _{k\in v}\sum _{j\in c}{x}_{ijk}=1,\forall i\in c\text{\hspace{1em}(3)}$$
$$\sum _{j\in c}{x}_{0jk}=1,\forall k\in v\text{\hspace{1em}(4)}$$
$$\sum _{i\in c}{x}_{ihk}-\sum _{j\in c}{x}_{hjk}=0,\forall h\in c,\forall k\in v\text{\hspace{1em}(5)}$$
$$\sum _{i\in c}{x}_{j0k}=1,\forall k\in v\text{\hspace{1em}(6)}$$
其中，式（2）分别表示总行车路程最短、车辆数最少、表示单辆车走的最大路程最短，式（3）表示每个顾客被访问且只访问一次，式（4）、式（5）、式（6）表示每辆车都从配送中心除法并以配送中心为重点，途径若干不重复的顾客。

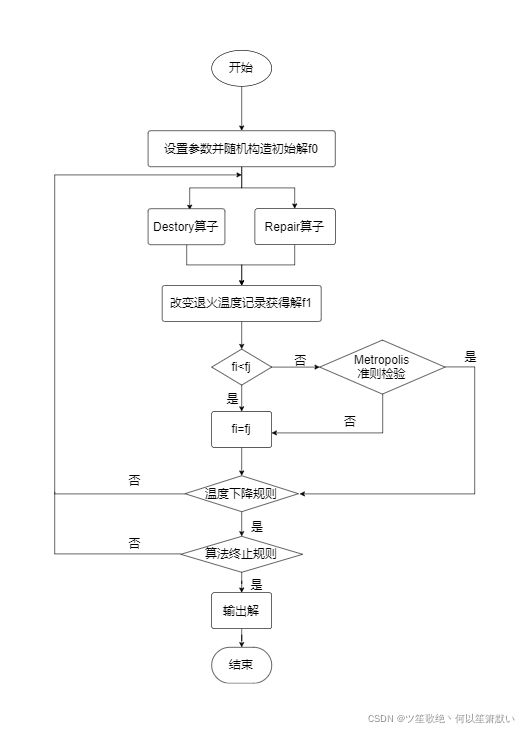
2.模拟退火算法模型

模拟退火(simulated annealing ,SA)算法是一种全局统计优化方法，是最适合解决车辆路径问题的算法之一。它最早由Metropoli[4]提出，是从物质的物理退火过程中得到启发。退火过程大致是:先将物体不断加热至高温，温度越高物质内部的粒子活跃性越高，且处于高速转动的不稳定状态，此时物质具有较高的内能然后缓慢降温，原子运动速度随着温度的下降减慢活跃度下降，物质的内能下降最后，整个物体达到内能最低，变成稳定的状态。
SA算法迭代优化寻找最优解的过程中，首先需要确定一个初始温度T_0,设置参数，并以问题解空间的初始状态作为初始解，然后在一定温度下，对当前解进行搜索算子干扰，模拟固体内部粒子的状态转移过程。之后比较在干扰后状态下得出的新解和当前解，依据Metropolis准则进行替换。该算法准则是以概率1来接受适应度值中的最优解，以一定的概率来接受适应值中的较差点。Metropolis准则的这种特殊能力使得算法不易陷入局部最优停滞，具有跳出局部获得全局最优解的能力。Metropolis准则定义为：
$$P_{ij}^T=\{\begin{array}{ll}1& ,E(j)\le E(i)\\ e^{-[\frac{E(j)-E(i)}{KT}]}=e^{-(\frac{\Delta E}{KT})}& ,\text{otrhers}\end{array}\text{\hspace{1em}(7)}$$
SA算法的迭代过程就是Markov链的生成过程，Markov链的长度L_k表示Metropolis算法第k次迭代时产生的变换个数。在控制参数t的衰减函数己选定的前提下，Markov链长应保证算法在控制参数的每一取值上解的概率分布趋于平稳分布。有限序列{L_k}规定了算法进程搜索的解空间范围。L_k与t_k密切相关，当 时， ，因此，为避免SA算法在温度较低时产生过长Markov链，可在每一温度下，算法选取相同的迭代次数，即采用固定L_k长度的方法，或是通过接受和拒绝的比率来控制迭代次数。
算法的停止准则，即控制参数t的终值t_final，或是终止温度T_final。合理的停止准则既要确保算法收敛于某一近似解，又要使最终解具有一定的质量。常用的停止准则可以设定为一个很小的终止温度T_f，或是给定一个确定的总迭代次数(Markov链的个数)，再或是解在连续若干Markov链中无变化等。
其算法流程图为：

---

源代码

Models

定义一些需要调用的类

class Sol():
    def __init__(self):
        self.nodes_seq=None
        self.obj=None
        self.routes=None
class Node():
    def __init__(self):
        self.id=0
        self.name=''
        self.seq_no=0
        self.x_coord=0
        self.y_coord=0
        self.demand=0
class Model():
    def __init__(self):
        self.best_sol=None
        self.node_list=[]
        self.node_seq_no_list=[]
        self.best_sol_list = []
        self.depot=None
        self.number_of_nodes=0
        self.opt_type=0
        self.vehicle_cap=0
        self.tem_best_sol = None
        self.wrong_count = 0
        self.current_distance = 0
        self.reheart = False
        self.distance_martix = None

utils

from math import sqrt, exp
from models import Sol, Node, Model
from copy import deepcopy
import random
import numpy as np
import matplotlib.pyplot as plt


class SA():

    # 初始化
    def __init__(self):
        self.Tstart = 30000         # 初始温度
        self.Tend = 1               # 终止温度
        self.alpha = 0.98           # 降温系数
        self.Tnow = 0               # 当前温度
        self.temp_iter = 300        # 迭代次数
        self.cont = 4               # 重新加热次数
        self.model = None           # 值类型为Model()
        self.file_path = './data/A-n32-k5.vrp'         # 文件路径

    # 生成初始解
    def __auxiliaryPredefine(self):
        # 初始化
        self.model = Model()
        self.model.opt_type = 1
        readVRPFile(self.file_path, self.model)
        distanceMatrix(self.model)
        nodes_seq = genInitSol(self.model.node_seq_no_list)      # 随机初始化解集
        distance, routes_list = calObj(nodes_seq, self.model)    # 对初始化解集寻解
        self.model.best_sol = Sol()    # 最优解
        self.model.best_sol.routes = deepcopy(routes_list)
        self.model.best_sol.obj = deepcopy(distance)
        # self.model.best_sol_list.append(self.model.best_sol)

    def __simulatedAnnealing(self):
        self.Tnow = self.Tstart
        temp_sol = self.model.best_sol_list[0]
        for sol in self.model.best_sol_list:
            if sol.obj <= temp_sol.obj:
                temp_sol = deepcopy(sol)
        self.model.best_sol = deepcopy(temp_sol)        
        while self.Tnow > self.Tend:
            currect_sol = deepcopy(self.model.best_sol)
            self.model.tem_distance = self.model.best_sol.obj
            for _ in range(self.temp_iter):
                temp_sol = Sol()    # 当前解
                # routes_list = deepcopy(self.model.best_sol.routes)
                routes_list = deepcopy(currect_sol.routes)
                new_routes_list, pop_nodes = randomPop(routes_list, self.model)
                temp_sol.routes, temp_sol.obj = rebuildList(
                    new_routes_list, pop_nodes, self.model)
                delta = temp_sol.obj - currect_sol.obj
                if delta < 0 or (delta > 0 and random.random() > exp(-delta / self.Tnow)):
                    currect_sol = deepcopy(temp_sol)
                if self.model.current_distance == currect_sol.obj:
                    self.model.wrong_count += 1
                else:
                    self.model.wrong_count = 0
                if self.model.best_sol.obj > currect_sol.obj:
                    self.model.best_sol = deepcopy(currect_sol)
                    self.model.wrong_count = 0
                self.model.current_distance = currect_sol.obj
            print(
                f'current temperature :   {self.Tnow:.2f}, currentValue: {currect_sol.obj:.2f}, bestValue: {self.model.best_sol.obj:.2f}', end='\r')
            self.Tnow *= self.alpha
            # self.model.best_sol_list.append(self.model.best_sol)
        self.model.tem_best_sol = deepcopy(self.model.best_sol)
        print()
        # print(self.model.best_sol.routes)

    def run(self):
        print('Begin')
        self.__auxiliaryPredefine()
        self.__simulatedAnnealing()
        showInfo(self.model)
        saveToFile(self.model)
        print('End')


def readVRPFile(file_path, model):
    node_seq_no = -1
    with open(file_path, 'r') as f:
        text = f.readlines()
    # 提取数据
    for i in range(len(text)):
        if 'DIMENSION' in text[i]:
            index = text[i].index(':') + 1
            model.number_of_nodes = eval(text[i][index:])   # 需求节点数量
        if 'CAPACITY' in text[i]:
            index = text[i].index(':') + 1
            model.vehicle_cap = eval(text[i][index:])       # 车辆最大载重
        if 'NODE_COORD_SECTION' in text[i]:
            i += int(text[-3])
            for _ in range(model.number_of_nodes):
                node_seq_no += 1
                node = Node()
                node_info = text[i].split()                 # 拆分数据
                node.id = node_seq_no                       # id
                node.x_coord = eval(node_info[1])           # x坐标
                node.y_coord = eval(node_info[2])           # y坐标
                node.seq_no = node_seq_no                   # 映射物理节点
                node.demand = eval(
                    text[i + model.number_of_nodes + 1].split()[1])  # 物理节点需求
                if node.demand == 0:
                    model.depot = node                      # 该点为车辆基地节点
                else:
                    model.node_list.append(node)            # 添加节点信息到列表
                    model.node_seq_no_list.append(node.seq_no)  # 添加节点id到列表
                i += 1
            break
    model.number_of_nodes = len(model.node_list)        # 更新需求节点数量

# 计算距离函数
def calDistance(route, model, cal_type=1):          # 计算总距离
    distance = 0
    if cal_type == 0:
        depot = model.depot
        for i in range(len(route) - 1):
            from_node = model.node_list[route[i]]
            to_node = model.node_list[route[i + 1]]
            distance += int(sqrt((from_node.x_coord - to_node.x_coord)
                            ** 2 + (from_node.y_coord - to_node.y_coord) ** 2))
        first_node = model.node_list[route[0]]
        last_node = model.node_list[route[-1]]
        distance += int(sqrt((depot.x_coord - last_node.x_coord)
                        ** 2 + (depot.y_coord - last_node.y_coord) ** 2))
        distance += int(sqrt((depot.x_coord - first_node.x_coord)
                        ** 2 + (depot.y_coord - first_node.y_coord) ** 2))
        return distance
    elif cal_type == 1:
        route = [tem + 1 for tem in route]
        route.insert(0, 0)
        route.append(0)
        for i in range(len(route) - 1):
            distance += model.distance_martix[route[i]][route[i + 1]]
        return distance
    else:
        print('Type{}IsNotDefine'.format(cal_type))
        return None


def calAllDistance(node_seq_list, model, cal_type=1):
    distance = 0
    for route in node_seq_list:
        route = [tem - 1 for tem in route]
        distance += calDistance(route, model, cal_type=cal_type)
    return distance


def distanceMatrix(model):      # 创建距离矩阵
    coord_matrix = [[model.depot.x_coord, model.depot.y_coord]]
    for i in range(model.number_of_nodes):
        coord_matrix.append([model.node_list[i].x_coord,
                            model.node_list[i].y_coord])
    distance_martix = np.zeros((len(coord_matrix), len(coord_matrix)))
    for i in range(len(coord_matrix)):
        for j in range(len(coord_matrix)):
            distance = int(sqrt((coord_matrix[i][0] - coord_matrix[j][0]) ** 2 + (
                coord_matrix[i][1] - coord_matrix[j][1]) ** 2))
            distance_martix[i][j] = distance
    model.distance_martix = distance_martix


# 辅助函数——解的初始化
def genInitSol(node_seq_no_list):                           # 随机生成初始解
    node_seq = deepcopy(node_seq_no_list)
    random.seed(random.randint(0, 10))
    random.shuffle(node_seq)
    return node_seq


def calGroup(node_seq, model):                              # 分组
    routes_list = []                                        # 定义解集
    route = []                                              # 定义路线
    real_cap = model.vehicle_cap                            # 车辆最大载荷
    num_of_vhicle = 0                                       # 车辆数
    for node_id in node_seq:
        if(real_cap - model.node_list[node_id-1].demand) >= 0:
            route.append(node_id)
            real_cap -= model.node_list[node_id-1].demand
        else:
            routes_list.append(route)
            route = [node_id]
            num_of_vhicle += 1
            real_cap = model.vehicle_cap - \
                model.node_list[node_id-1].demand  # 重置
    routes_list.append(route)
    return routes_list, num_of_vhicle


def calObj(nodes_seq, model):                           # 由输出类型求对应解
    routes_list, num_of_vhicle = calGroup(nodes_seq, model)
    if model.opt_type == 0:
        return num_of_vhicle, routes_list
    elif model.opt_type == 1:
        distance = 0
        for route in routes_list:
            route = [tem - 1 for tem in route]
            distance += calDistance(route, model, cal_type=1)
        return distance, routes_list
    else:
        print('Type{}IsNotDefine'.format(model.opt_type))
        return None


def changeToList(dit):
    change_list = []
    for key, value in dit.items():
        change_list.append(value)
    change_list = [change_list[len(change_list)-1 - i]
                   for i in range(len(change_list))]
    return change_list


def randomShufft(nodes_seq_list):
    all_nodes_list = deepcopy(nodes_seq_list)
    random.seed(random.randint(0, 10))
    for nodes_list in all_nodes_list:
        random.shuffle(nodes_list)
    return all_nodes_list

# 随机弹出算子
def randomPop(node_seq_list, model):
    new_node_seq_list = deepcopy(node_seq_list)
    pop_dit = {}
    for i in range(len(new_node_seq_list)):
        pop_id = random.randint(0, len(new_node_seq_list[i]) - 1)
        if len(new_node_seq_list[i]) <= 1:
            continue
        else:
            if pop_id == 0:
                model.tem_distance -= (model.distance_martix[0][new_node_seq_list[i][0]]+model.distance_martix[new_node_seq_list[i]
                                       [0]][new_node_seq_list[i][1]]-model.distance_martix[0][new_node_seq_list[i][1]])
            elif pop_id == (len(new_node_seq_list[i])-1):
                model.tem_distance -= (model.distance_martix[new_node_seq_list[i][pop_id-1]][new_node_seq_list[i][pop_id]] +
                                       model.distance_martix[new_node_seq_list[i][pop_id]][0]-model.distance_martix[new_node_seq_list[i][pop_id-1]][0])
            else:
                model.tem_distance -= (model.distance_martix[new_node_seq_list[i][pop_id-1]][new_node_seq_list[i][pop_id]]+model.distance_martix[new_node_seq_list[i]
                                       [pop_id]][new_node_seq_list[i][pop_id+1]]-model.distance_martix[new_node_seq_list[i][pop_id-1]][new_node_seq_list[i][pop_id+1]])
            pop_dit[i] = new_node_seq_list[i].pop(pop_id)
    pop_nodes = changeToList(pop_dit)
    return new_node_seq_list, pop_nodes

# 重新建立列表算子
def rebuildList(nodes_seq_list, pop_nodes, model, distance=None):
    new_nodes_seq_list = deepcopy(nodes_seq_list)
    index1, index2 = -1, -1
    # for key, value in pop_nodes.items():
    for value in pop_nodes:
        # new_distance_tem = calAllDistance(new_nodes_seq_list, model)
        min_distance = float('inf')
        for i in range(len(new_nodes_seq_list)):
            # if i == key:
            #     continue
            temp_route = deepcopy(new_nodes_seq_list[i])
            temp_route.append(value)
            if isSuitable(temp_route, model):
                for temp in range(len(temp_route)):
                    new_route = deepcopy(new_nodes_seq_list[i])
                    new_route.insert(temp, value)
                    # cal_distance_list = [tem - 1 for tem in new_route]
                    # distance_tem = calDistance(cal_distance_list, model)
                    if temp == 0:
                        distance_tem = model.distance_martix[0][new_route[0]] + \
                            model.distance_martix[new_route[0]][new_route[1]]-model.distance_martix[0][new_route[1]]
                    elif temp == (len(temp_route) - 1):
                        distance_tem = model.distance_martix[new_route[temp-1]][new_route[temp]] + \
                            model.distance_martix[new_route[temp]][0] - \
                            model.distance_martix[new_route[temp-1]][0]
                    else:
                        distance_tem = model.distance_martix[new_route[temp-1]][new_route[temp]] + model.distance_martix[new_route[temp]][new_route[temp+1]]-model.distance_martix[new_route[temp-1]][new_route[temp+1]]
                    # distance_tem = calAllDistance(new_nodes_seq_list, model)
                    if distance_tem < min_distance:
                        min_distance = distance_tem
                        index1, index2 = i, temp
        new_nodes_seq_list[index1].insert(index2, value)
        model.tem_distance += min_distance
    return new_nodes_seq_list, model.tem_distance

# 定义变化值函数
def evaluationFunction(nodes_list, model, original_distance):
    tem_distance = calAllDistance(nodes_list, model)
    return tem_distance - original_distance


def randomDisturbance(random_list):
    node_seq = deepcopy(random_list)
    random.seed(random.randint(0, 10))
    random.shuffle(node_seq)
    return node_seq


def isSuitable(route, model):
    vehicle_cap = model.vehicle_cap
    route = [tem - 1 for tem in route]
    for node_id in route:
        vehicle_cap -= model.node_list[node_id].demand
    if vehicle_cap < 0:
        return False
    else:
        return True

# 寻找最优结果
def findBestValue(model):
    temp_best = model.best_sol_list[0]
    for sol in model.best_sol_list:
        if sol.obj <= temp_best.obj:
            temp_best = sol
    return temp_best

# 保存结果到文件
def saveToFile(model):
    model.best_sol = deepcopy(findBestValue(model))
    write_lines = []
    write_lines.append('bestValue: {}'.format(model.best_sol.obj))
    write_lines.append('solutions:')
    for route in model.best_sol.routes:
        line = '0->'
        for i in route:
            line += '{}->'.format(i)
        line += '0'
        write_lines.append(line)
    with open('result.txt', 'w') as f:
        for line in write_lines:
            f.write(line + '\n')

# 展示优化结果
def showInfo(model):
    model.best_sol = deepcopy(findBestValue(model))
    for route in model.best_sol.routes:
        print('0', end='->')
        for i in route:
            print(i, end='->')
        print('0')
    print(f'bestValue : {model.best_sol.obj}')
    draw(model)

# 绘图
def draw(model):
    # 绘制Depot & Nodes
    routeX, routeY = [node.x_coord for node in model.node_list], [
        node.y_coord for node in model.node_list]
    routeX.append(model.depot.x_coord)
    routeY.append(model.depot.y_coord)
    plt.scatter(routeX, routeY, marker='o')
    # 绘制Routes
    for i in range(len(model.best_sol.routes)):
        routeX, routeY = [model.depot.x_coord], [model.depot.y_coord]
        for id in model.best_sol.routes[i]:
            routeX.append(model.node_list[id - 1].x_coord)
            routeY.append(model.node_list[id - 1].y_coord)
        routeX.append(routeX[0])
        routeY.append(routeY[0])
        plt.plot(routeX, routeY)
    plt.show()

Python实现结果

file: A-n32-k5.vrp
bestValue: 774.0
solutions:
0->27->24->0
0->18->8->9->22->15->29->10->25->5->20->0
0->12->1->16->30->0
0->6->3->2->23->28->4->11->14->0
0->26->7->21->31->19->17->13->0

总结

第一次写长篇大论的文章，代码总有些瑕疵，还请批评指正。