Pytorch入门笔记（一）

• Author：ZERO-A-ONE
• Date：2021-03-04

本人最近在学习一些神经网络的相关知识，需要用到Pytorch这个机器学习的库，故做一些笔记来方便学习，主要是参考了知乎用户Sherlock的10分钟快速入门Pytorch：https://zhuanlan.zhihu.com/p/26893755

一、环境搭建

​ 这里我选用的平台是Anaconda，只要安装好了Anaconda再安装Pytorch或者Tensorflow-gpu都是非常简单的事情

1.1 安装Anaconda

​ 先安装一些必备的库

$ sudo apt-get install python3 python3-pip python3-dev git libssl-dev libffi-dev build-essential

​ 然后从官网里面下载Anaconda的安装脚本

$ wget https://repo.anaconda.com/archive/Anaconda3-2020.11-Linux-x86_64.sh

​ 然后给脚本赋予执行权限

$ chmod +x Anaconda3-2020.11-Linux-x86_64.sh

​ 然后运行安装脚本即可

$ ./Anaconda3-2020.11-Linux-x86_64.sh

这里不建议使用root权限安装，如果你自己使用的用户就不是root账户的话

​ 这里如果出现找不到conda命令的情况可能需要手动修改shell的环境配置

$ sudo vim ~/.bashrc

​ 然后就修改为类似这样的实际安装路径

export PATH="/home/ubuntu/anaconda3/bin:$PATH"

​ 然后刷新重新运行

$ source ~/.bashrc

1.2 Pytorch

​ 只需要运行这一条命令即可创建虚拟环境

$ conda create -n pytorch3.8-gpu python=3.8

​ 然后记住下面两条命令

Executing transaction: done
#
# To activate this environment, use
#
#     $ conda activate pytorch3.8-gpu
#
# To deactivate an active environment, use
#
#     $ conda deactivate

​ 先执行这条指令进入Anaconda环境中

$ source activate

​ 执行第一条指令就可以进入虚拟环境中

$ conda activate pytorch3.8-gpu

​ 然后进行安装环境

$ conda install pytorch torchvision cudatoolkit=10.1 -c pytorch

​ 进行测试

(pytorch3.8-gpu) ubuntu@VM-0-4-ubuntu:~/MachLE$ python
Python 3.8.8 (default, Feb 24 2021, 21:46:12)
[GCC 7.3.0] :: Anaconda, Inc. on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> import torch
>>> torch.cuda.is_available()
True
>>>

二、基础概念

2.1 基础组件

2.1.1 Tensor（张量）

张量是PyTorch里的基本运算单位，与numpy的ndarray相同都表示一个多维的矩阵。与ndarray最大的区别在于Tensor能使用GPU加速，而ndarray只能用在CPU上。大家可以把Pytorch中的Tensor理解为可以在GPU上计算的Numpy array。相比array，Tensor提供了其他的一些与深度学习息息相关的操作，如：Tensor可以追踪一个计算图和梯度

orch定义了七种CPU tensor类型和八种GPU tensor类型：

Data tyoe	CPU tensor	GPU tensor
32-bit floating point	torch.FloatTensor	torch.cuda.FloatTensor
64-bit floating point	torch.DoubleTensor	torch.cuda.DoubleTensor
16-bit floating point	N/A	torch.cuda.HalfTensor
8-bit integer (unsigned)	torch.ByteTensor	torch.cuda.ByteTensor
8-bit integer (signed)	torch.CharTensor	torch.cuda.CharTensor
16-bit integer (signed)	torch.ShortTensor	torch.cuda.ShortTensor
32-bit integer (signed)	torch.IntTensor	torch.cuda.IntTensor
64-bit integer (signed)	torch.LongTensor	torch.cuda.LongTensor

torch.Tensor是默认的tensor类型（torch.FlaotTensor）的简称

Tensor主要拥有以下初始化方法：

• torch.rand(*size) : 使用[0, 1]均匀分布随机初始化
• torch.randn(*size) : 服从正太分布初始化
• torch.zeros(*size): 使用0填充
• torch.ones(*size)：使用1填充
• torch.eye(*size)：初始化一个单位矩阵，即对角线为1，其余为0

Tensor也可以和numpy互相进行转换，将Tensor转换成numpy，只需调用.numpy()方法即可。将numpy转换成Tensor，使用torch.from_numpy()进行转换

# a --> Tensor
a = torch.rand(3, 2)
# Tensor --> numpy
numpy_a = a.numpy()
# numpy --> Tensor
b = torch.from_numpy(numpy_a)

Tensor还可以放入GPU进行GPU级别的运算，提升运算速度

# 判断一下电脑是否支持GPU
torch.cuda.is_available()


a = torch.rand(5, 4)
a = a.cuda()
print(a)

2.1.2 Variable（变量）

pytorch和numpy不一样的地方就来了，就是其提供了自动求导功能，也就是可以自动给你你要的参数的梯度，这个操作又另外一个基本元素提供，Variable

Variable就是变量的意思。实质上也就是可以变化的量，区别于int变量，它是一种可以变化的变量，这正好就符合了反向传播，参数更新的属性

具体来说，在pytorch中的Variable就是一个存放会变化值的地理位置，里面的值会不停发生变化，就像一个装鸡蛋的篮子，鸡蛋数会不断发生变化。那谁是里面的鸡蛋呢，自然就是pytorch中的tensor了。（也就是说，pytorch都是有tensor计算的，而tensor里面的参数都是Variable的形式）。如果用Variable计算的话，那返回的也是一个同类型的Variable

• Tensor不能反向传播
• Variable可以反向传播

本质上Variable和Tensor没有区别，不过Variabel会放入一个计算图，然后进行前向传播，反向传播以及自动求导

一个机器学习任务的核心是模型的定义以及模型的参数求解方式，对这两者进行抽象之后，可以确定一个唯一的计算逻辑，将这个逻辑用图表示，称之为计算图。计算图表现为有向无环图，定义了数据的流转方式，数据的计算方式，以及各种计算之间的相互依赖关系等

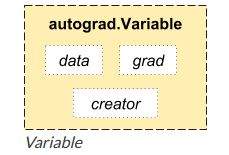
一个Variable里面包含着三个属性，data，grad和creator，其中creator表示得到这个Variabel的操作，比如乘法或者加法等等，grad表示方向传播的梯度，data表示取出这个Variabel里面的数据

一个简单的使用例子就是：

from torch.autograd import Variable

# requires_grad 表示是否对其求梯度，默认是False
x = Variable(torch.Tensor([3]), requires_grad=True)
y = Variable(torch.Tensor([5]), requires_grad=True)
z = 2 * x + y + 4

# 对 x 和 y 分别求导
z.backward()

# x 的导数和 y 的导数
print('dz/dx: {}'.format(x.grad.data))
print('dz/dy: {}'.format(y.grad.data))

运算的结果就是

dz/dx: 
 2
[torch.FloatTensor of size 1]

dz/dy: 
 1
[torch.FloatTensor of size 1]

Variable还有一些常用的参数：

• requires_grad：variable默认是不需要被求导的，即requires_grad属性默认为False，如果某一个节点的requires_grad为True，那么所有依赖它的节点requires_grad都为True

• volatile：variable的volatile属性默认为False，如果某一个variable的volatile属性被设为True，那么所有依赖它的节点volatile属性都为True。volatile属性为True的节点不会求导，volatile的优先级比requires_grad高

• retain_graph：多次反向传播（多层监督）时，梯度是累加的。一般来说，单次反向传播后，计算图会free掉，也就是反向传播的中间缓存会被清空【这就是动态度的特点】。为进行多次反向传播需指定retain_graph=True来保存这些缓存

• backward()：反向传播，求解Variable的梯度。放在中间缓存中

我们还可以获取Variable里面的数据，将其变成tensor形式

print(variable)  # Variable 形式
"""
Variable containing:
 1 2
 3 4
[torch.FloatTensor of size 2x2]
"""
 
print(variable.data) # 将variable形式转为tensor 形式
"""
 1 2
 3 4
[torch.FloatTensor of size 2x2]
"""
 
print(variable.data.numpy()) # numpy 形式
"""
[[ 1. 2.]
 [ 3. 4.]]
"""

2.1.3 Autograd

PyTorch中的Autograd模块实现了深度学习的算法中的反向传播求导数，在Tensor上的所有操作，Autograd都能为它们自动计算微分，简化了手动求导数的过程

**autograd是pytorch中的一个套件 ，**当使用autograd时，神经网络的前向传播会定义一个计算图（computational graph），该图中，node是tensor，edge是函数（produce output from input）；在这个graph中进行反向传播可以很容易计算梯度

具体的，如果x是一个tensor，也是graph中的一个node，如果有：x.requires_grad=True，那么x.grad将会是另一个tensor，其中包含了求导后的梯度值

autograd机制主要提供了两个函数，forward和backward，forward从输入tensor计算得到一个输出tensor；backward接受输出tensor相对于某个标量值的梯度，然后进一步计算出输入tensor相对于该同一个标量的梯度

在张量创建时，通过设置requires_grad = True来告诉PyTorch需要对该张量进行自动求导，PyTorch会记录该张量的每一步操作历史并自动计算导数。requires_grad默认为False

x = torch.randn(5, 5, requires_grad = True)

在计算完成后，调用backward()方法会自动根据历史操作来计算梯度，并保存在grad中

2.1.4 nn（神经网络包）

pytorch里面的模型建立，模型的建立主要依赖于torch.nn和 torch.nn.functional，torch.nn包含这个所有神经网络的层的结构torch.nn是专门为神经网络设计的模块化接口，建立在Autogard之上

通常一个神经网络类需要继承nn.Module，并实现forward方法，PyTorch就会根据autograd自动实现backward方法

torch.nn.functional 表示的是直接对其做一次向前运算操作

一个比较简单的网络结构如代码所示

from torch import nn
import torch.nn.functional as F
# 基本的网络构建类模板
class net_name(nn.Module):
    def __init__(self):
        super(net_name, self).__init__()
        # 可以添加各种网络层
        self.conv1 = nn.Conv2d(3, 10, 3)
        # 具体每种层的参数可以去查看文档
        
    def forward(self, x):
        # 定义向前传播
        out = self.conv1(x)
        return out

一个稍微复杂的网络层定义是：

import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()

        # 卷积层
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)

        # 全连接层
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # 卷积 --> ReLu --> 池化
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        x = F.max_pool2d(F.relu(self.conv2(x)), (2, 2))

        # reshape, '-1'表示自适应
        # x = (n * 16 * 5 * 5) --> n : batch size
        # x.size()[0] == n --> batch size
        x = x.view(x.size()[0], -1)

        # 全连接层
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)

        return x

2.1.5 损失函数

在torch.nn中还定义了一些常用的损失函数，比如MESLoss(均方误差)，CrossEntropyLoss(交叉熵误差)等

labels = torch.arange(10).view(1, 10).float()
out = net(input)
criterion = nn.MSELoss()
# 计算loss
loss = criterion(labels, out)

2.1.6 优化器(torch.optim)

在反向传播计算完所有参数的梯度后，还需要使用优化方法来更新网络的参数，常用的优化方法有随机梯度下降法(SGD)，策略如下：

weight = weight - learning_rate * gradient

import torch.optim
import torch.nn as nn

out = net(input)
criterion = nn.MSELoss(out, labels)
# 新建一个优化器，SGD只需要输入要调整的参数和学习率
optimizer = torch.optim.SGD(net.parameters(), lr = 0.01)
# 反向传播前，先梯度清0, optimizer.zero_grad()等同于net.zero_grad()
optimizer.zero_grad()
loss.backward()

# 更新参数
optimizer.step()

2.2 网络层

2.2.1 卷积层

卷积：Conv2d

'''
in_channels:输入通道数

out_channels：输出通道数

kernel_size：卷积核尺寸，整数或者元组

stride：卷积操作的步幅，整数或者元组

padding：数据hw方向上填充的层数，整数或者元组，默认填充的是0

dilation：卷积核内部各点的间距，整数或者元组

groups：控制输入和输出之间的连接；group=1，输出是所有输入的卷积；
group=2，此时相当于有并排的两个卷积层，每个卷积层计算输入通道的一半，
并且产生的输出是输出通道的一半，随后将这两个输出连接起来。

bias：bool类型，为true的话就会对输出添加可学习的偏置量

padding_mode：填充模式，字符串类型
'''
torch.nn.Conv2d(in_channels, out_channels, 
                kernel_size, stride=1, 
                padding=0, dilation=1, 
                groups=1, bias=True, 
                padding_mode='zeros')

转置卷积：ConvTranspose2d

'''
in_channels:输入通道数
out_channels：输出通道数
kernel_size：卷积核尺寸，整数或者元组
stride：卷积操作的步幅，整数或者元组
padding：数据hw方向上填充的层数，整数或者元组，默认填充的是0
output_padding：对输出的hw填充的层数，整数或者元组

groups：控制输入和输出之间的连接；group=1，输出是所有输入的卷积；
group=2，此时相当于有并排的两个卷积层，每个卷积层计算输入通道的一半，
并且产生的输出是输出通道的一半，随后将这两个输出连接起来。

dilation：卷积核内部各点的间距，整数或者元组
bias：bool类型，为true的话就会对输出添加可学习的偏置量
padding_mode：填充模式，字符串类型
'''
torch.nn.ConvTranspose2d(in_channels, out_channels, 
                         kernel_size, stride=1, 
                         padding=0, output_padding=0, 
                         groups=1, bias=True, 
                         dilation=1, padding_mode='zeros')

2.2.2 池化层

最大池化：MaxPool2d

'''
kernel_size:窗口尺寸；整数或者元组

stride：窗口的步幅，默认就等于窗口尺寸；整数或者元组

padding：数据hw方向上的零填充层数；整数或者元组

dilation：一个控制窗口中元素步幅的参数；整数或者元组

return_indices：如果等于True，会返回输出最大值的序号，对于上采样操作会有帮助

ceil_mode：如果等于True，计算输出数据的hw的时候，
会使用向上取整，代替默认的向下取整的操作
'''
torch.nn.MaxPool2d(kernel_size, stride=None, 
                   padding=0, dilation=1, 
                   return_indices=False, ceil_mode=False)

平均池化：AvgPool2d

'''
kernel_size:窗口尺寸；整数或者元组

stride：窗口的步幅，默认就等于窗口尺寸；整数或者元组

padding：数据hw方向上的零填充层数；整数或者元组

ceil_mode：如果等于True，计算输出数据的hw的时候，
会使用向上取整，代替默认的向下取整的操作

count_include_pad:如果等于True，计算平均池化时，将包括padding填充的0

divisor_override
'''
torch.nn.AvgPool2d(kernel_size, stride=None, 
                   padding=0, ceil_mode=False, 
                   count_include_pad=True, 
                   divisor_override=None)

2.2.3 填充层

零填充：ZeroPad2d

'''
padding:填充的层数，整数或者元组；如果是一个整数值n，
那么在四个边界上都填充n层0；如果是四个整数值组成的元组，
那么就分别表示对应方向上填充0的层数，对应关系如下：
(padding_left,padding_right,padding_top,padding_bottom)
'''
torch.nn.ZeroPad2d(padding)

2.2.4 非线性激活层

ELU

torch.nn.ELU(alpha=1.0, inplace=False)

LeakyReLU

torch.nn.LeakyReLU(negative_slope=0.01, inplace=False)

SELU

torch.nn.SELU(inplace=False)

RReLU

torch.nn.RReLU(lower=0.125, upper=0.3333333333333333, inplace=False)

PReLU（系数可学习）

'''
num_parameters:可学习参数的个数，1或者通道数；
1表示所有通道使用相同的可学习系数，后者表示每个通道独有一个可学习系数

init：可学习系数a的初始值
'''
torch.nn.PReLU(num_parameters=1, init=0.25)

Sigmoid

torch.nn.Sigmoid

2.2.5 全连接层

Linear layers

class torch.nn.Linear(in_features, out_features, bias=True)

对输入数据做线性变换：y=Ax+by=Ax+b

参数：

• in_features - 每个输入样本的大小
• out_features - 每个输出样本的大小
• bias - 若设置为False，这层不会学习偏置。默认值：True

形状：

• 输入: (N,in_features)(N,in_features)
• 输出： (N,out_features)(N,out_features)

变量：

• weight -形状为(out_features x in_features)的模块中可学习的权值
• bias -形状为(out_features)的模块中可学习的偏置

2.2.6 标准化层

BatchNorm2d

'''
num_features:来自期望输入的特征数，该期望输入的大小为
'batch_size x num_features x height x width'

eps:为保证数值稳定性（分母不能趋近或取0）,给分母加上的值。默认为1e-5

momentum:动态均值和动态方差所使用的动量,默认为0.1

affine:一个布尔值，当设为true，给该层添加可学习的仿射变换参数
'''
torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, 
                     affine=True, track_running_stats=True)

2.2.7 Dropout丢弃层

• 输入： (N,C,H,W)
  输出： (N,C,H,W)（与输入形状相同）

'''
p：将元素置0的概率，默认值=0.5
'''
torch.nn.Dropout(p=0.5, inplace=False)

2.2.8 Upsample 上采样

• 对给定的1D (temporal), 2D (spatial) or 3D (volumetric)数据进行上采样，这里的维度不包括batch和channel

'''
size:根据给定的需要进行上采样的数据的维度，指定的输出数据的size；
对应上面所说的三种维度，size可以是int,(int,int),(int,int,int)

scale_factor:指定在某个维度上输出为输入尺寸的多少倍，
对应上面所说的三种维度，size可以是float,(float,float),(float,float,float)

mode：可使用的上采样算法，有'nearest', 'linear', 'bilinear', 
'bicubic' and 'trilinear'. 默认使用'nearest'

align_corners：如果为True，输入的角像素将与输出张量对齐，因此将保存下
来这些像素的值。仅当使用的算法为'linear', 'bilinear'or 
'trilinear'时可以使用。默认设置为False
'''
torch.nn.Upsample(size=None, scale_factor=None, 
                  mode='nearest', align_corners=None)

三、实战：线性回归

编写一个简单的机器学习网络主要是经过以下步骤：

• data：准备数据
• model：建立网络模型
• train：训练模型
• validation：验证模型

3.1 data

首先我们需要给出一系列的点作为线性回归的数据，使用numpy来存储这些点：

x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168],
                    [9.779], [6.182], [7.59], [2.167], [7.042],
                    [10.791], [5.313], [7.997], [3.1]], dtype=np.float32)

y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573],
                    [3.366], [2.596], [2.53], [1.221], [2.827],
                    [3.465], [1.65], [2.904], [1.3]], dtype=np.float32)

我们需要将numpy转换成Tensor，因为Tensor才是Pytorch能够处理的数据类型

x_train = torch.from_numpy(x_train)
y_train = torch.from_numpy(y_train)

3.2 model

接下来我们需要编写一个线性回归模型，也就是写一个网络模型出来

class LinearRegression(nn.Module):
    def __init__(self):
        super(LinearRegression, self).__init__()
        self.linear = nn.Linear(1, 1)  # input and output is 1 dimension

    def forward(self, x):
        out = self.linear(x)
        return out
model = LinearRegression()

这个网络模型就比较简单，只有一层线性层，nn.Linear表示的是 y=w*x+b，里面的两个参数都是1，表示的是x是1维，y也是1维。意思就是输入和输出都是1纬向量，例如x=[3.3]，y=[1.7]

然后需要定义loss和optimizer，就是误差和优化函数

criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-4)

这里的误差函数criterion使用的是最小二乘loss，之后我们做分类问题更多的使用的是cross entropy loss，交叉熵

优化函数使用的是随机梯度下降，注意需要将model的参数model.parameters()传进去让这个函数知道他要优化的参数是那些

3.3 train

接着开始训练

num_epochs = 1000
for epoch in range(num_epochs):
    inputs = Variable(x_train)
    target = Variable(y_train)

    # forward
    out = model(inputs) # 前向传播
    loss = criterion(out, target) # 计算loss
    # backward
    optimizer.zero_grad() # 梯度归零
    loss.backward() # 方向传播
    optimizer.step() # 更新参数

    if (epoch+1) % 20 == 0:
        print('Epoch[{}/{}], loss: {:.6f}'.format(epoch+1,
                                                  num_epochs,
                                                  loss.data[0]))

第一个循环表示每个epoch，接着开始前向传播，然后计算loss，然后反向传播，接着优化参数，特别注意的是在每次反向传播的时候需要将参数的梯度归零，即

optimzier.zero_grad()

3.4 validation

训练完成之后我们就可以开始测试模型了

model.eval()
predict = model(Variable(x_train))
predict = predict.data.numpy()

3.5 完整的代码

import matplotlib.pyplot as plt
import numpy as np
import torch
from torch import nn
from torch.autograd import Variable

x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168],
                    [9.779], [6.182], [7.59], [2.167], [7.042],
                    [10.791], [5.313], [7.997], [3.1]], dtype=np.float32)

y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573],
                    [3.366], [2.596], [2.53], [1.221], [2.827],
                    [3.465], [1.65], [2.904], [1.3]], dtype=np.float32)


x_train = torch.from_numpy(x_train)

y_train = torch.from_numpy(y_train)


# Linear Regression Model
class linearRegression(nn.Module):
    def __init__(self):
        super(linearRegression, self).__init__()
        self.linear = nn.Linear(1, 1)  # input and output is 1 dimension

    def forward(self, x):
        out = self.linear(x)
        return out


model = linearRegression()
# 定义loss和优化函数
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-4)

# 开始训练
num_epochs = 1000
for epoch in range(num_epochs):
    inputs = x_train
    target = y_train

    # forward
    out = model(inputs)
    loss = criterion(out, target)
    # backward
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if (epoch+1) % 20 == 0:
        print(f'Epoch[{epoch+1}/{num_epochs}], loss: {loss.item():.6f}')

model.eval()
with torch.no_grad():
    predict = model(x_train)
predict = predict.data.numpy()

fig = plt.figure(figsize=(10, 5))
plt.plot(x_train.numpy(), y_train.numpy(), 'ro', label='Original data')
plt.plot(x_train.numpy(), predict, label='Fitting Line')
# 显示图例
plt.legend() 
plt.show()

# 保存模型
torch.save(model.state_dict(), './linear.pth')

Pytorch具有两种模型保存方式：

只保存模型参数：

# 保存
torch.save(model.state_dict(), '\parameter.pkl')
# 加载
model = TheModelClass(...)
model.load_state_dict(torch.load('\parameter.pkl'))

保存完整模型

# 保存
torch.save(model, '\model.pkl')
# 加载
model = torch.load('\model.pkl')

PyTorch 中，一个模型(torch.nn.Module)的可学习参数(也就是权重和偏置值)是包含在模型参数(model.parameters())中的，一个状态字典就是一个简单的 Python 的字典，其键值对是每个网络层和其对应的参数张量。模型的状态字典只包含带有可学习参数的网络层（比如卷积层、全连接层等）和注册的缓存（batchnorm的 running_mean）。优化器对象(torch.optim)同样也是有一个状态字典，包含的优化器状态的信息以及使用的超参数。

由于状态字典也是 Python 的字典，因此对 PyTorch 模型和优化器的保存、更新、替换、恢复等操作都很容易实现