为什么80%的码农都做不了架构师？>>>

朴素贝叶斯分类器

维基百科，自由的百科全书

跳转到：导航、搜索

本条目的引用需要进行清理
参考文献应符合正确的引用、脚注或外部链接格式。

朴素贝叶斯分类器是一种应用基于独立假设的贝叶斯定理的简单概率分类器.更精确的描述这种潜在的概率模型为独立特征模型。

简介

简单来说，朴素贝叶斯分类器假设样本每个特征与其他特征都不相关。举个例子，如果一种水果其具有红，圆，直径大概4英寸等特征，该水果可以被判定为是苹果。

尽管这些特征相互依赖或者有些特征由其他特征决定，然而朴素贝叶斯分类器认为这些属性在判定该水果是否为苹果的概率分布上独立的。朴素贝叶斯分类器依靠精确的自然概率模型，在有监督学习的样本集中能获取得非常好的分类效果。在许多实际应用中，朴素贝叶斯模型参数估计使用最大似然估计方法，换而言之朴素贝叶斯模型能工作并没有用到贝叶斯概率或者任何贝叶斯模型。

尽管是带着这些朴素思想和过于简单化的假设，但朴素贝叶斯分类器在很多复杂的现实情形中仍能够取得相当好的效果。2004年，一篇分析贝叶斯分类器问题的文章揭示了朴素贝叶斯分类器取得看上去不可思议的分类效果的若干理论上的原因。^[1] 尽管如此，2006年有一篇文章详细比较了各种分类方法，发现更新的方法（如boosted trees和随机森林）的性能超过了贝叶斯分类器。^[2] 朴素贝叶斯分类器的一个优势在于只需要根据少量的训练数据估计出必要的参数（变量的均值和方差）。由于变量独立假设，只需要估计各个变量的方法，而不需要确定整个协方差矩阵。

朴素贝叶斯概率模型

理论上，概率模型分类器是一个条件概率模型。

$p(C \vert F_1,\dots,F_n)\,$

独立的类别变量有若干类别，条件依赖于若干特征变量 ,,...,。但问题在于如果特征数量较大或者每个特征能取大量值时，基于概率模型列出概率表变得不现实。所以我们修改这个模型使之变得可行。贝叶斯定理有以下式子：

$p(C \vert F_1,\dots,F_n) = \frac{p(C) \ p(F_1,\dots,F_n\vert C)}{p(F_1,\dots,F_n)}. \,$

用朴素的语言可以表达为：

$\mbox{posterior} = \frac{\mbox{prior} \times \mbox{likelihood}}{\mbox{evidence}}. \,$

实际中，我们只关心分式中的分子部分，因为分母不依赖于而且特征的值是给定的，于是分母可以认为是一个常数。这样分子就等价于联合分布模型。

$p(C \vert F_1, \dots, F_n)\,$

重复使用链式法则，可将该式写成条件概率的形式，如下所示：

$p(C \vert F_1, \dots, F_n)\,$ $\varpropto p(C) \ p(F_1,\dots,F_n\vert C)$ $\varpropto p(C) \ p(F_1\vert C) \ p(F_2,\dots,F_n\vert C, F_1)$ $\varpropto p(C) \ p(F_1\vert C) \ p(F_2\vert C, F_1) \ p(F_3,\dots,F_n\vert C, F_1, F_2)$ $\varpropto p(C) \ p(F_1\vert C) \ p(F_2\vert C, F_1) \ p(F_3\vert C, F_1, F_2) \ p(F_4,\dots,F_n\vert C, F_1, F_2, F_3)$ $\varpropto p(C) \ p(F_1\vert C) \ p(F_2\vert C, F_1) \ p(F_3\vert C, F_1, F_2) \ \dots p(F_n\vert C, F_1, F_2, F_3,\dots,F_{n-1}).$

现在“朴素”的条件独立假设开始发挥作用:假设每个特征对于其他特征, $j\neq i$ 是条件独立的。这就意味着

$p(F_i \vert C, F_j) = p(F_i \vert C)\,$

对于 $i\ne j$ ，所以联合分布模型可以表达为

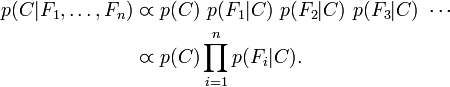
$\begin{align} p(C \vert F_1, \dots, F_n) & \varpropto p(C) \ p(F_1\vert C) \ p(F_2\vert C) \ p(F_3\vert C) \ \cdots\, \\& \varpropto p(C) \prod_{i=1}^n p(F_i \vert C).\,\end{align}$

这意味着上述假设下，类变量的条件分布可以表达为：

$p(C \vert F_1,\dots,F_n) = \frac{1}{Z} p(C) \prod_{i=1}^n p(F_i \vert C)$

其中(证据因子)是一个只依赖与 $F_1,\dots,F_n$ 等的缩放因子，当特征变量的值已知时是一个常数。由于分解成所谓的类先验概率和独立概率分布 $p(F_i\vert C)$ ，上述概率模型的可掌控性得到很大的提高。如果这是一个分类问题，且每个 $p(F_i\vert C=c)$ 可以表达为个参数，于是相应的朴素贝叶斯模型有(k − 1) + n r k个参数。实际应用中，通常取（二分类问题）， (伯努利分布作为特征），因此模型的参数个数为，其中是二值分类特征的个数。

参数估计

所有的模型参数（例如，类的先验概率和特征的概率分布）都可以通过训练集的相关频率来估计。这些方法是概率的最大似然估计。类的先验概率可以通过假设各类等概率来计算（先验概率 = 1 / (类的数量)），或者通过训练集的各类样本出现的次数来估计（A类先验概率=（A类样本的数量）/(样本总数)）。为了估计特征的分布参数，我们要先假设训练集数据满足某种分布或者非参数模型。^[3] 如果要处理的是连续数据一种通常的假设是这些连续数值为高斯分布。例如，假设训练集中有一个连续属性，。我们首先对数据根据类别分类，然后计算每个类别中的均值和方差。令 $\mu_c$ 表示为在c类上的均值，令 $\sigma^2_c$ 为在c类上的方差。在给定类中某个值的概率，，可以通过将表示为均值为 $\mu_c$ 方差为 $\sigma^2_c$ 正态分布计算出来。如下， $P(x=v|c)=\tfrac{1}{\sqrt{2\pi\sigma^2_c}}\,e^{ -\frac{(v-\mu_c)^2}{2\sigma^2_c} }$ 处理连续数值问题的另一种常用的技术是通过离散化连续数值的方法。通常，当训练样本数量较少或者是精确的分布已知时，通过概率分布的方法是一种更好的选择。在大量样本的情形下离散化的方法表现更优，因为大量的样本可以学习到数据的分布。由于朴素贝叶斯是一种典型的用到大量样本的方法（越大计算量的模型可以产生越高的分类精确度），所以朴素贝叶斯方法都用到离散化方法，而不是概率分布估计的方法。

样本修正

如果一个给定的类和特征值在训练集中没有一起出现过，那么基于频率的估计下该概率将为0。这将是一个问题因为与其他概率相乘时将会把其他概率的信息统统去除。所以常常要求要对每个小类样本的概率估计进行修正，以保证不会出现有为0的概率出现。

从概率模型中构造分类器

讨论至此为止我们导出了独立分布特征模型，也就是朴素贝叶斯概率模型。朴素贝叶斯分类器包括了这种模型和相应的决策规则。一个普通的规则就是选出最有可能的那个：这就是大家熟知的最大后验概率（MAP）决策准则。相应的分类器便是如下定义的 $\mathrm{classify}$ 公式：

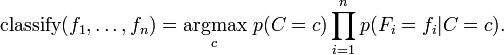
$\mathrm{classify}(f_1,\dots,f_n) = \underset{c}{\operatorname{argmax}} \ p(C=c) \displaystyle\prod_{i=1}^n p(F_i=f_i\vert C=c).$

讨论

尽管实际上独立假设常常是不准确的，但朴素贝叶斯分类器的若干特性让其在实践中能够取得令人惊奇的效果。特别地，各类条件特征之间的解耦意味着每个特征的分布都可以独立地被当做一维分布来估计。这样减轻了由于维数灾带来的阻碍,当样本的特征个数增加时就不需要使样本规模呈指数增长。然而朴素贝叶斯在大多数情况下不能对类概率做出非常准确的估计，但在许多应用中这一点并不要求。例如，朴素贝叶斯分类器中，依据最大后验概率决策规则只要正确类的后验概率比其他类要高就可以得到正确的分类。所以不管概率估计轻度的甚至是严重的不精确都不影响正确的分类结果。在这种方式下，分类器可以有足够的鲁棒性去忽略朴素贝叶斯概率模型上存在的缺陷。关于朴素贝叶斯能取得成功的其他原因将会在后文中进一步讨论。

实例

性别分类

问题描述:通过一些测量的特征，包括身高、体重、脚的尺寸，判定一个人是男性还是女性。

训练

训练数据如下：

性别	身高(英尺)	体重(磅)	脚的尺寸(英尺)
男	6	180	12
男	5.92 (5'11")	190	11
男	5.58 (5'7")	170	12
男	5.92 (5'11")	165	10
女	5	100	6
女	5.5 (5'6")	150	8
女	5.42 (5'5")	130	7
女	5.75 (5'9")	150	9

假设训练集样本的特征满足高斯分布，得到下表：

性别	均值(身高)	方差(身高)	均值(体重)	方差(体重)	均值(脚的尺寸)	方差(脚的尺寸)
男性	5.855	3.5033e-02	176.25	1.2292e+02	11.25	9.1667e-01
女性	5.4175	9.7225e-02	132.5	5.5833e+02	7.5	1.6667e+00

我们认为两种类别是等概率的，也就是P(male)= P(female) = 0.5。在没有做辨识的情况下就做这样的假设并不是一个好的点子。但我们通过数据集中两类样本出现的频率来确定P(C)，我们得到的结果也是一样的。

测试

以下给出一个待分类是男性还是女性的样本。

性别	身高(英尺)	体重(磅)	脚的尺寸(英尺)
sample	6	130	8

我们希望得到的是男性还是女性哪类的后验概率大。男性的后验概率通过下面式子来求取

$posterior (male) = \frac{P(male) \, p(height | male) \, p(weight | male) \, p(foot size | male)}{evidence}$

女性的后验概率通过下面式子来求取

$posterior (female) = \frac{P(female) \, p(height | female) \, p(weight | female) \, p(foot size | female)}{evidence}$

证据因子（通常是常数）用来是各类的后验概率之和为1.

证据因子是一个常数（在正态分布中通常是正数），所以可以忽略。接下来我们来判定这样样本的性别。

$p(\mbox{height} | \mbox{male}) = \frac{1}{\sqrt{2\pi \sigma^2}}\exp\left(\frac{-(6-\mu)^2}{2\sigma^2}\right) \approx 1.5789$ ,其中 $\mu = 5.855$ ， $\sigma^2 = 3.5033e^{-02}$ 是训练集样本的正态分布参数. 注意，这里的值大于1也是允许的 – 这里是概率密度而不是概率，因为身高是一个连续的变量.

$p(weight | male) = 5.9881e^{-06}$ $p(foot size | male) = 1.3112e^{-3}$ $posterior numerator (male) = 6.1984e^{-09}$

$p(height | female) = 2.2346e^{-1}$ $p(weight | female) = 1.6789e^{-2}$ $p(foot size | female) = 2.8669e^{-1}$ $posterior numerator (female) = 5.3778e^{-04}$

由于女性后验概率的分子比较大，所以我们预计这个样本是女性。

文本分类

这是一个用朴素贝叶斯分类做的一个文本分类问题的例子。考虑一个基于内容的文本分类问题，例如判断邮件是否为垃圾邮件。想像文本可以分成若干的类别，首先文本可以被一些单词集标注，而这个单词集是独立分布的，在给定的C类文本中第i个单词出现的概率可以表示为：

$p(w_i \vert C)\,$

（通过这种处理，我们进一步简化了工作，假设每个单词是在文中是随机分布的-也就是单词不依赖于文本的长度，与其他词出现在文中的位置，或者其他文本内容。）

对于一个给定类别C，单词的文本D，概率表示为

$p(D\vert C)=\prod_i p(w_i \vert C)\,$

我们要回答的问题是文档D属于类C的概率是多少。换而言之 $p(C \vert D)\,$ 是多少？现在定义

$p(D\vert C)={p(D\cap C)\over p(C)}$ $p(C\vert D)={p(D\cap C)\over p(D)}$

通过贝叶斯定理将上述概率处理成似然度的形式

$p(C\vert D)={p(C)\over p(D)}\,p(D\vert C)$ 假设现在只有两个相互独立的类别， S和¬ S（垃圾邮件和非垃圾邮件），这里每个元素（邮件）要么是垃圾邮件，要么就不是。 $p(D\vert S)=\prod_i p(w_i \vert S)\,$ $p(D\vert\neg S)=\prod_i p(w_i\vert\neg S)\,$

Using the Bayesian result above, we can write: 用上述贝叶斯的结果，可以写成

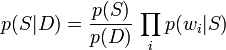
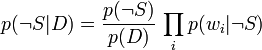
$p(S\vert D)={p(S)\over p(D)}\,\prod_i p(w_i \vert S)$ $p(\neg S\vert D)={p(\neg S)\over p(D)}\,\prod_i p(w_i \vert\neg S)$

两者相除:

${p(S\vert D)\over p(\neg S\vert D)}={p(S)\,\prod_i p(w_i \vert S)\over p(\neg S)\,\prod_i p(w_i \vert\neg S)}$

整理得:

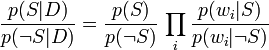
${p(S\vert D)\over p(\neg S\vert D)}={p(S)\over p(\neg S)}\,\prod_i {p(w_i \vert S)\over p(w_i \vert\neg S)}$

这样概率比p(S | D) / p(¬S | D)可以表达为似然比。实际的概率p(S | D)可以很容易通过log (p(S | D) / p(¬S | D))计算出来，基于p(S | D) + p(¬S | D) = 1。

结合上面所讨论的概率比，可以得到：

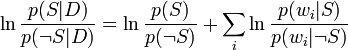
$\ln{p(S\vert D)\over p(\neg S\vert D)}=\ln{p(S)\over p(\neg S)}+\sum_i \ln{p(w_i\vert S)\over p(w_i\vert\neg S)}$

(这种对数似然比的技术在统计中是一种常用的技术。在这种两个独立的分类情况下（如这个垃圾邮件的例子），把对数似然比转化为sigmoid curve的形式)。

最后文本可以分类，当 $p(S\vert D) > p(\neg S\vert D)$ 或者 $\ln{p(S\vert D)\over p(\neg S\vert D)} > 0$ 时判定为垃圾邮件，否则为正常邮件。

参见

AODE
Bayesian spam filtering
Bayesian network
Random naive Bayes
线性分类器
Boosting
模糊逻辑
Logistic regression
Class membership probabilities
Neural network
Predictive analytics
Perceptron
支持向量机
贝叶斯定理
有监督学习
Classifier (mathematics)
最大似然估计
贝叶斯概率
boosted trees
随机森林

参考文献

^ Harry Zhang "The Optimality of Naive Bayes". FLAIRS2004 conference. (available online: PDF)
^ Caruana, R. and Niculescu-Mizil, A.: "An empirical comparison of supervised learning algorithms". Proceedings of the 23rd international conference on Machine learning, 2006. (available online [1])
^ George H. John and Pat Langley (1995). Estimating Continuous Distributions in Bayesian Classifiers. Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence. pp. 338-345. Morgan Kaufmann, San Mateo.

外部链接

Book Chapter: Naive Bayes text classification, Introduction to Information Retrieval
Naive Bayes for Text Classification with Unbalanced Classes
Benchmark results of Naive Bayes implementations
Hierarchical Naive Bayes Classifiers for uncertain data (an extension of the Naive Bayes classifier).
winnowTag Create tags that run Bayesian classifiers on over 1/2

million items updated from 7,500 feeds.

Online application of a Naive Bayes classifier^{[失效链接]} (emotion modelling), with a full explanation.
dANN: Naive Classifier - Explanation and Example
BayesNews - Bayesian RSS Reader (useful for personal news

clipping).

Naive Bayes in PMML
classifiers-to-document-classification-problems Simple example of document classification with Naive Bayes, implemented in Ruby
Document Classification Using Naive Bayes Classifier with Perl

Software

IMSL Numerical Libraries Collections of math and statistical algorithms available in

C/C++, Fortran, Java and C#/.NET. Data mining routines in the IMSL Libraries include a Naive

Bayes classifier.

Orange, a free data mining software suite, module

orngBayes

Winnow content recommendation Open source Naive Bayes

text classifier works with very small training and unbalanced training sets. High performance,

C, any Unix.

Naive Bayes implementation in Visual Basic (includes executable and source code).
An interactive Microsoft Excel spreadsheet

Naive Bayes implementation using VBA (requires enabled macros)

with viewable source code.

jBNC - Bayesian Network Classifier Toolbox
POPFile Perl-based email proxy system classifies email

into user-defined "buckets", including spam.

Statistical Pattern Recognition Toolbox for Matlab.
sux0r An Open Source Content management system with a focus

on Naive Bayesian categorization and probabilistic content.

ifile - the first freely available (Naive)

Bayesian mail/spam filter

NClassifier - NClassifier is a .NET library that

supports text classification and text summarization. It is a port of the Nick Lothian's

popular Java text classification engine, Classifier4J.

Classifier4J - Classifier4J is a Java library

designed to do text classification. It comes with an implementation of a Bayesian classifier,

and now has some other features, including a text summary facility.

MALLET - A Java package for document classification and other

natural language processing tasks.

nBayes - nBayes is an open source .NET library written in C#
Apache Mahout - Machine learning package offered by Apache Open

Source

Weka - Popular open source machine learning package,

written in Java

C# implementation of Naive Bayes used for

documents categorization that includes files processing, stop words filtering and stemming.

Same site offers comparison to other algorithms.

Bayes-Classfier/View-details.html OpenPR-NB - A C++ implementation of Naive Bayes Classifier.

It supports both multinomial and multivariate Bernoulli event model. The maximum likelihood

estimate with a Laplace smoothing is used for learning parameters.

Publications

Domingos, Pedro & Michael Pazzani (1997) "On the optimality of the simple Bayesian

classifier under zero-one loss". Machine Learning, 29:103–137. (also online at

CiteSeer:

[2])

Rish, Irina. (2001). "An empirical study of the naive Bayes classifier". IJCAI 2001 Workshop

on Empirical Methods in Artificial Intelligence. (available online:

PDF,

PostScript)

Hand, DJ, & Yu, K. (2001). "Idiot's Bayes - not so stupid after all?" International

Statistical Review. Vol 69 part 3, pages 385-399. ISSN 0306-7734.

Webb, G. I., J. Boughton, and Z. Wang (2005).

Not So Naive Bayes: Aggregating One- Dependence Estimators. Machine Learning 58(1). Netherlands: Springer, pages 5–24.

Mozina M, Demsar J, Kattan M, & Zupan B. (2004). "Nomograms for Visualization of Naive

Bayesian Classifier". In Proc. of PKDD-2004, pages 337-348. (available online:

PDF)

Maron, M. E. (1961). "Automatic Indexing: An Experimental Inquiry." Journal of the ACM

(JACM) 8(3):404–417. (available online:

key1=321084&key2=9636178211&coll=GUIDE&dl=ACM&CFID=56729577&CFTOKEN=37855803 PDF)

Minsky, M. (1961). "Steps toward Artificial Intelligence." Proceedings of the IRE 49(1):8-

30.

McCallum, A. and Nigam K. "A Comparison of Event Models for Naive Bayes Text

Classification". In AAAI/ICML-98 Workshop on Learning for Text Categorization, pp. 41–

48. Technical Report WS-98-05. AAAI Press. 1998. (available online:

PDF)

Rennie J, Shih L, Teevan J, and Karger D. Tackling The Poor Assumptions of Naive Bayes

Classifiers. In Proceedings of the Twentieth International Conference on Machine Learning

(ICML). 2003. (available online: PDF)

类别:分类算法类别:贝叶斯统计类别:统计分类

朴素贝叶斯分类器

朴素贝叶斯分类器

目录

简介

朴素贝叶斯概率模型

参数估计

样本修正

从概率模型中构造分类器

讨论

实例

性别分类

训练

测试

文本分类

参见

参考文献

外部链接

你可能感兴趣的:(人工智能,java,c#)