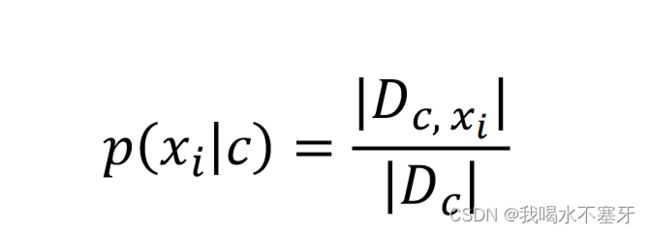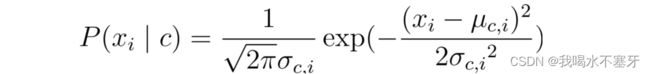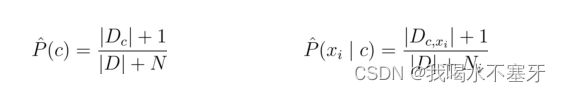【机器学习】朴素贝叶斯算法
目录
一、实现原理
1、贝叶斯定理
2、朴素贝叶斯分类器
3、拉普拉斯修正
二、代码
一、实现原理
1、贝叶斯定理
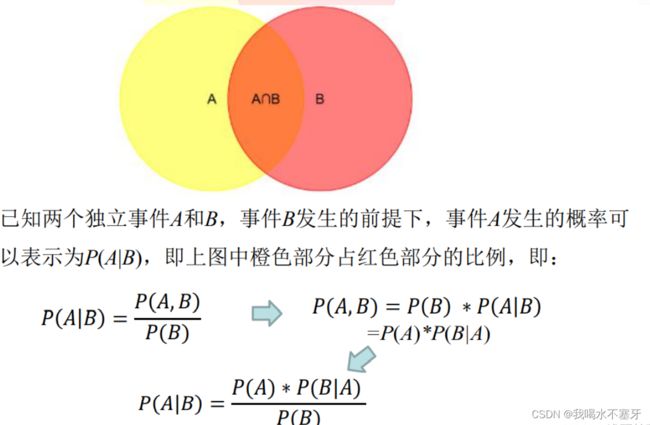
朴素贝叶斯是基于概率的一种推断,先展示公式:
其中,P(A)是先验概率,就是在事件B发生之前,我们对A事件概率的一个判断;
P(A|B)是后验概率,是在B事件发生之后,我们对A事件概率的重新评估;
P(B|A)/P(B)是可能性函数,这是一个调整因子,使得预估概率更接近真实概率。
2、朴素贝叶斯分类器
朴素贝叶斯分类器(Naïve Bayes Classifier)采用了“属性条件独立性假设”,即每个属性独立地对分类结果发生影响。
朴素贝叶斯分类器的训练器的训练过程就是基于训练集D估计类先验概率P(c),并为每个属性估计条件概率 P(x_i│c)。
令D_c表示训练集D中第c类样本组合的集合,则类先验概率:
对离散属性,令D_c,x_i表示D_c中在第 i 个属性上取值为x_i的样本组成的集合,则条件概率P(x_i│c)可估计为:
对连续属性,可考虑概率密度函数,假定p(x_i│c)~N(μ_c,i,σ_c,i^2),其中μ_c,i和σ_c,i^2分别是第 c类样本在第i个属性上取值的均值和方差,则有:
3、拉普拉斯修正
若某个属性值在训练集中没有与某个类同时出现过,则训练后的模型会出现 over-fitting 现象。比如“敲声=清脆”测试例,训练集中没有该样例,因此连乘式计算的概率值为0,无论其他属性上明显像好瓜,分类结果都是“好瓜=否”,这显然不合理。
为了避免其他属性携带的信息,被训练集中未出现的属性值“抹去”,在估计概率值时通常要进行“拉普拉斯修正”:
令 N 表示训练集 D 中可能的类别数,N_i表示第i个属性可能的取值数,则贝叶斯公式可修正为:
二、代码
实例:垃圾邮件分类
import numpy as np
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
# 预处理数据
def text_parse(big_string):
token_list = big_string.split()
return [tok.lower() for tok in token_list if len(tok)>2]
# 去除列表中重复元素,并以列表形式返回
def create_vocab_list(data_set):
vocab_set = set({})
for d in data_set:
vocab_set = vocab_set | set(d)
return list(vocab_set)
# 统计每一文档(或邮件)在单词表中出现的次数,并以列表形式返回
def words_to_vec(vocab_list, input_set):
return_vec = [0] * len(vocab_list)
for word in input_set:
if word in vocab_list:
return_vec[vocab_list.index(word)] += 1
return return_vec
# 朴素贝叶斯主程序
doc_list, class_list, x = [], [], []
for i in range(1, 26):
# 读取第i篇垃圾文件,并以列表形式返回
word_list = text_parse(open('email/spam/{0}.txt'.format(i), encoding='ISO-8859-1').read())
doc_list.append(word_list)
class_list.append(1)
# 读取第i篇非垃圾文件,并以列表形式返回
word_list = text_parse(open('email/ham/{0}.txt'.format(i), encoding='ISO-8859-1').read())
doc_list.append(word_list)
class_list.append(0)
# 将数据向量化
vocab_list = create_vocab_list(doc_list)
for word_list in doc_list:
x.append(words_to_vec(vocab_list, word_list))
# 分割数据为训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, class_list, test_size=0.25)
x_train, x_test, y_train, y_test = np.array(x_train), np.array(x_test),\
np.array(y_train), np.array(y_test)
print("x_train: ")
print(x_train[:5])
print("\n")
print("y_train: ")
print(y_train[:5])
print("\n")
# 训练模型
nb_model = MultinomialNB()
nb_model.fit(x_train, y_train)
# 测试模型效果
y_pred = nb_model.predict(x_test)
# 输出预测情况
print("正确值:{0}".format(y_test))
print("预测值:{0}".format(y_pred))
print("准确率:%f%%" % (accuracy_score(y_test, y_pred)*100))结果如下所示,识别正确率为92.3%,效果还算可以哦。
x_train:
[[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]]
y_train:
[1 0 0 0 1]
正确值:[1 1 1 1 1 1 1 1 1 1 1 0 0]
预测值:[1 1 1 0 1 1 1 1 1 1 1 0 0]
准确率:92.307692%