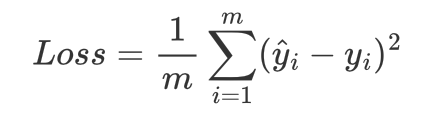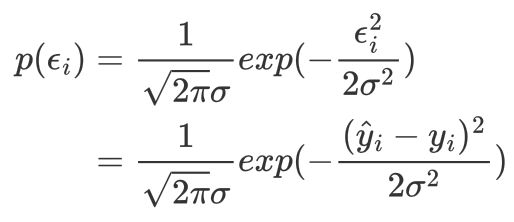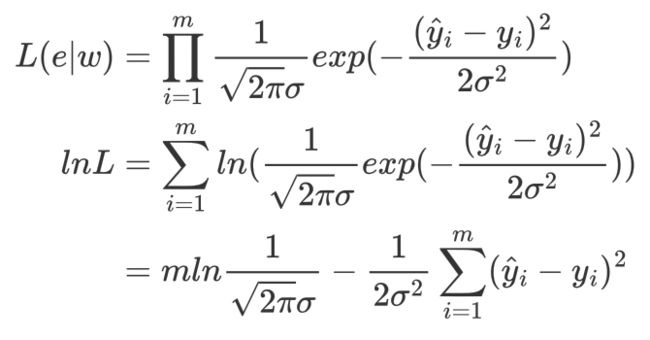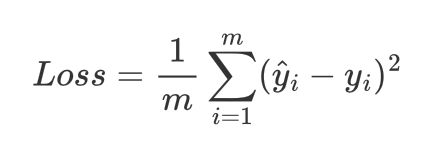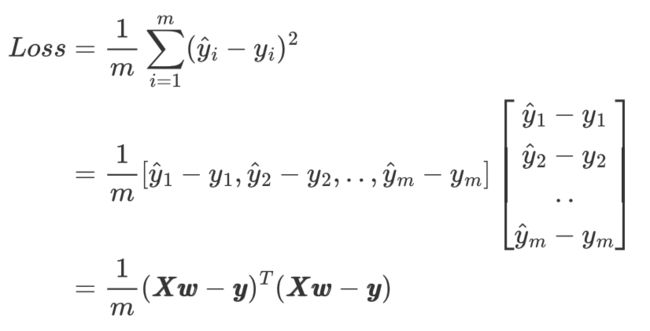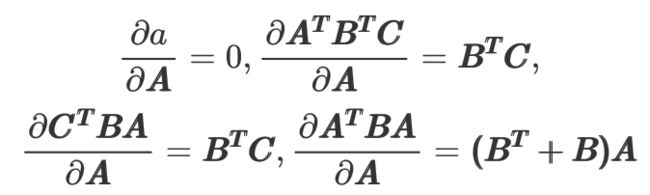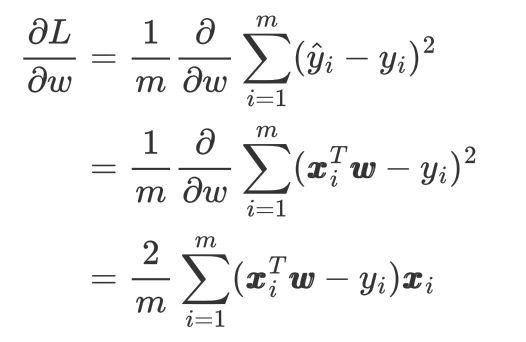线性回归公式推导及代码实现（非调包）

本文转载至本人原创公众号《算法实验室》，欢迎关注，有问题可随时联系，转载请注明出处。

原文链接：线性回归公式推导及代码实现

一、概述

本文有以下几个方面构成，在每一部分都给出了详细的公式推导及numpy代码。

①、线性回归的累加及矩阵公式；

②、损失函数的表达（MSE、极大似然估计）；

③、损失函数求解（最小二乘法，梯度下降法）；

④、sklearn的代码求解

⑤、总结

        本文所有的向量都默认为列向量，粗体均表示向量或矩阵。 xij 表示第 i 个样本的第 j 个特征，设共有 m 个样本 n 个特征，其中 w0 为偏置项b， xi0 表示第 i 个样本的第0个特征，为1， xi表示第 i 个样本。

①线性回归的累加形式表达式为：

②矩阵形式的表达式为：

二、损失函数

下面介绍两种得到线性回归损失函数的思路：

1、MSE

        要想最后拟合的结果比较好，那么要保证函数实际值与估计值之间的差距小，也即，

        使得上式结果最小的参数 w即为最优解，但是绝对值对于求导等计算不太方便，所以采用取平方计算，同时为了使得损失函数不至于太大除以样本数m，所以上式的损失函数等价于下式（如果不除以样本量，那么在数据量特别多的情况下，损失函数计算的的结果过大，不利于计算，以及后面采用梯度下降算法更新迭代时，所需的每步的步长就需要特别小）：

        将该损失函数称作MSE（Mean Squared Error）均方误差。

2、极大似然估计

        上面讲述了得到损失函数的第一种方式，下面从概率的角度讲解第二种方式。

        由于是拟合结果，真实值与估计值之间总是存在误差的。真实值可以表示为估计值与误差的和:

        由于误差是一个随机变量，他是符合均值为0，方差为的 σ2 高斯分布。对于第i个样本误差的概率密度为：

        那么如何求得参数w的最优值呢？我们可以从极大似然估计的角度来考虑，极大似然估计的基本思路就是假设未知参数已经定下来了，但是参数未知，所有样本发生的概率我们也能求出来，当取到某些特定的样本时概率最大的参数就是这个未知参数。换句话说，就是使样本最有可能发生的的情况下的参数。

        根据极大似然函数法，构建似然函数，似然函数的最大值就是参数w的最有可能的取值，具体过程如下：

要使似然函数最大也就是，最小化减号后面的项，所以最终的损失函数为：

同理，为了避免损失函数过大，在后面采用梯度下降算法时，除以样本数得到MSE：

代码如下：

#累加形式损失函数
def loss_function_sum(x,y,theta):
    a=np.dot(x,theta)-y
    return np.sum(a**2)/x.shape[0]

矩阵形式的损失函数：

代码如下：

#矩阵形式损失函数
def loss_function_matrix(x,y,theta):
    a=np.dot(x,theta)-y
    return np.dot(a.T,a)/x.shape[0]

        采用sklearn中的波士顿房价数据集验证损失函数是否一致。注意以下两点：

        ①、在文章一开始我就说了，所有向量默认为列向量，所以为了保证计算的正确性，一定要将所有向量变成默认的列向量形式。

        ②、在特征矩阵前拼接一个全为1的列向量表示偏置项。

import numpy as np
import pandas as pd
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler  
data=load_boston().data 
y=load_boston().target.reshape(-1,1)
data=StandardScaler().fit_transform(data) 
x0=np.ones([data.shape[0],1])  #构建全为1的列向量，与特征矩阵拼接
data=np.hstack([x0,data])
theta=np.ones(data.shape[1]).reshape(-1,1) #初始化theta，也就是参数w
print(loss_function_matrix(data,y,theta),loss_function_sum(data,y,theta))

        可以看出，损失给定任意参数w，损失函数的值一样，证明矩阵及向量形式的损失函数我们并没有写错，并且结果一样，因此为了方便，以后我们仅采用向量形式进行损失函数的代码编写。

三、损失函数求解

        下面采用两种方法来求解损失函数：最小二乘法、梯度下降法，并且每种方法分别采用累加和矩阵两种形式推导，并给出响应的python代码验证。

1、先导知识

为了对损失函数进行求导，需要有矩阵求导的先导知识：

2、 最小二乘法

        最小二乘法的思想就是高中数学的求极值的思想，对损失函数求导，令导函数（也就是梯度）为        0，求解的参数就是极值参数。

2.1、累加形式的梯度

2.2、矩阵形式的梯度

        令梯度为0，就是最小二乘法最后的结果，所以：

代码实现如下：

inv_matrix=np.linalg.inv(np.dot(data.T,data))
w=np.dot(inv_matrix,np.dot(data.T,y))  
print(w)

3、梯度下降

这里不再对梯度下降的原理进行过多阐述，总而言之就是利用梯度来不断迭代更新参数值，梯度迭代停止的条件有：

①、每次更新的梯度的值小于某一阈值；

②、两次迭代之间的差值小于某一阈值；

③、自定义迭代次数，达到这一次数时，迭代停止。

        梯度下降分为批量梯度下降（BGD）、随机梯度下降（SGD）、小批量梯度下降（MBGD）。

        首先先写出累加及矩阵形式的梯度下降函数：

#累加形式梯度函数
def gradient_function_sum(x,y,theta):
    sum=0
    for i in range(x.shape[0]):
        _=(np.dot(x[i,:],theta)-y[i] )*np.array(x[i,:]).reshape(-1,1)
        sum=sum+_ 
    return sum*2/x.shape[0]
    
#矩阵形式梯度函数
def gradient_function_matrix(x,y,theta):
    a=np.dot(x,theta)-y
    return 2*np.dot(x.T,a)/x.shape[0]

        以上两种形式所得到的的结果也是一模一样的，为了计算方便，下面仅采用矩阵表达式。

3.1、BGD

        BGD是一次利用所有样本进行计算，计算效率较低。其代码如下：

#限制迭代次数控制程序停止
def bgd_gradient_descent1(x,y, alpha,epoch):
    theta=np.ones(x.shape[1]).reshape(-1, 1)
    gradient = gradient_function_matrix(x,y,theta)
    for _ in range(epoch):
        theta=theta-alpha*gradient
        gradient = gradient_function_matrix(x,y,theta)
    return theta
        
#限制梯度的大小控制程序停止
def bgd_gradient_descent2(x,y, alpha):
    theta=np.ones(x.shape[1]).reshape(-1, 1)
    gradient = gradient_function_matrix(x,y,theta)
    while not all(np.abs(gradient) <= 1e-5):
        theta=theta-alpha*gradient 
        gradient = gradient_function_matrix(x,y,theta)
    return theta

3.2、SGD

        SGD是每次利用一个样本进行梯度迭代，所以运算效率高，但是也正是因为用一个样本来决定梯度方向，导致其梯度的方向变化很大，不能很快的收敛于全局或者局部最优值。代码如下：

def sgd(x,y, alpha):
    x=np.mat(x)
    y=np.mat(y)
    theta=np.ones(x.shape[1]).reshape(-1, 1)
    theta=np.mat(theta)
    k=np.random.randint(x.shape[0])  
    gradient = 2/x.shape[0]*x[k].T*(x[k]*theta-y[k]) 
    while not all(np.abs(gradient) <= 1e-5):
        theta=theta-alpha*gradient 
        gradient = gradient_function_matrix(x,y,theta)
    return theta

3.3、MBGD

        MBGD是每次利用部分样本进行迭代，是BGD与SGD的一个折中。代码如下：

def mbgd(x,y,alpha,frac):#frac为抽取样本的比例
    x=pd.DataFrame(x)
    theta=np.ones(x.shape[1]).reshape(-1, 1)
    theta=np.mat(theta)
    row=x.sample(frac=frac,replace=False).index 
    x=np.mat(x.loc[row,:])
    y=np.mat(y[[row]])
    gradient=2/x.shape[0]*x.T*(x*theta-y) 
    while not all(np.abs(gradient) <= 1e-5): 
        theta=theta-alpha*gradient 
        gradient = gradient_function_matrix(x,y,theta)
    return theta

四、sklearn求解

1、最小二乘法

from sklearn.linear_model import LinearRegression,SGDRegressor
data=load_boston().data 
y=load_boston().target  
data=StandardScaler().fit_transform(data) 
lr=LinearRegression()
lr.fit(data ,y)
print(lr.intercept_)
print(lr.coef_)

2、梯度下降法

data=load_boston().data 
y=load_boston().target  
data=StandardScaler().fit_transform(data)
lr=SGDRegressor()
lr.fit(data ,y)
print(lr.intercept_)
print(lr.coef_)

五、总结

        本文共讨论的线性回归的四种大方法：最小二乘法、BGD、SGD、MBGD，以及各种方法的矩阵及累加形式实现。

        通过运行以上代码可以看出，所有的方法求出来的结果基本上差别不大。