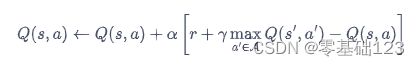【强化学习】
强化学习DQN
提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 强化学习DQN
- DQN算法的简介
- 一、环境的介绍
- 二、DQN算法
-
- 1、DQN算法的关键技术
- 2.DQN代码
-
-
-
- 2.1 导入库
- 2.2 定义类
- 2.3 训练画图
-
-
- 总结
DQN算法的简介
提示:这里可以添加本文要记录的大概内容:
DQN算法可以看作是Q_learning算法的改进,可以用来解决连续动作和离散动作的场景,当场景中的状态数量级很大的时候,计算机中存储Q表格不现实,因此采用函数拟合的方法来估计Q值,即将复杂的Q值表格视作数据,使用一个参数化的Q*来拟合这些数据。
这种函数拟合的方法存在一定的精度损失,因此被称为近似方法,下面的例子是DQN用来解决连续状态下离散动作的问题,将连续的状态进行离散化。
提示:以下是本篇文章正文内容,下面案例可供参考
一、环境的介绍
构建强化学习的环境是非常重要的,其中主要的两个因素是智能体的状态和智能体的动作。
使用的是 CartPole 环境,它的状态是连续的,动作是离散的,它的场景可以描述为:在车杆环境中,有一辆小车,智能体的任务是通过左右移动保持车上的杆竖直,若杆的倾斜度数过大,或者车子离初始位置左右的偏离程度过大,或者坚持时间到达 200 帧,则游戏结束。智能体的状态是一个维数为 4 的向量,每一维都是连续的,其动作是离散的,动作空间大小为 2。

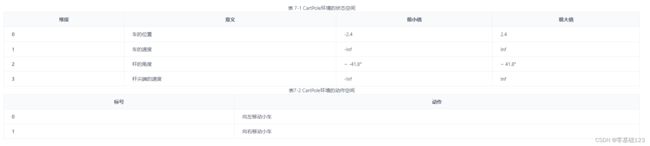
在游戏中每坚持一帧,智能体能获得分数为 1 的奖励,坚持时间越长,则最后的分数越高,坚持 200 帧即可获得最高的分数。
二、DQN算法
1、DQN算法的关键技术
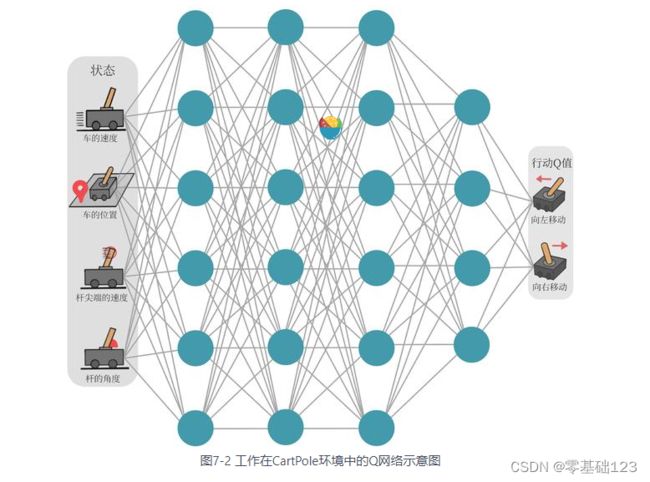
现在我们想在类似车杆的环境中得到动作价值函数,由于状态每一维度的值都是连续的,无法使用表格记录,因此一个常见的解决方法便是使用函数拟合(function approximation)的思想。由于神经网络具有强大的表达能力,因此我们可以用一个神经网络来表示函数Q。若动作是连续(无限)的,神经网络的输入是状态和动作,然后输出一个标量,表示在状态下采取动作能获得的价值。若动作是离散(有限)的,除了可以采取动作连续情况下的做法,我们还可以只将状态输入到神经网络中,使其同时输出每一个动作的Q值。通常 DQN(以及 Q-learning)只能处理动作离散的情况,因为在函数Q的更新过程中有MAXa这一操作。假设神经网络用来拟合函数w的参数是 ,即每一个状态s下所有可能动作a的值我们都能表示为Q(s,a)。我们将用于拟合函数Q函数的神经网络称为Q 网络,如图 7-2 所示。
Q_Learing 的更新规则:
我们可以将Q_Learing拓展到神经网络的形式–深度Q网络算法。由于DQN算法是离线的策略算法,因此可以使用贪婪搜索策略来平衡探索与利用,将收集到的数据存储起来,在后续的训练中使用。
DQN 中还有两个非常重要的模块——经验回放和目标网络,它们能够帮助 DQN 取得稳定、出色的性能。
2.DQN代码
接下来,我们就正式进入 DQN 算法的代码实践环节。我们采用的测试环境是 CartPole-v0,其状态空间相对简单,只有 4 个变量,因此网络结构的设计也相对简单:采用一层 128 个神经元的全连接并以 ReLU 作为激活函数。当遇到更复杂的诸如以图像作为输入的环境时,我们可以考虑采用深度卷积神经网络。
从 DQN 算法开始,我们将会用到rl_utils库,它包含一些专门为本书准备的函数,如绘制移动平均曲线、计算优势函数等,不同的算法可以一起使用这些函数。
2.1 导入库
代码如下(示例):
import random
import gym
import numpy as np
import collections
from tqdm import tqdm
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
import rl_utils
2.2 定义类
class ReplayBuffer:
''' 经验回放池 '''
def __init__(self, capacity):
self.buffer = collections.deque(maxlen=capacity) # 队列,先进先出
def add(self, state, action, reward, next_state, done): # 将数据加入buffer
self.buffer.append((state, action, reward, next_state, done))
def sample(self, batch_size): # 从buffer中采样数据,数量为batch_size
transitions = random.sample(self.buffer, batch_size)
state, action, reward, next_state, done = zip(*transitions)
return np.array(state), action, reward, np.array(next_state), done
def size(self): # 目前buffer中数据的数量
return len(self.buffer)
class Qnet(torch.nn.Module):
''' 只有一层隐藏层的Q网络 '''
def __init__(self, state_dim, hidden_dim, action_dim):
super(Qnet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x)) # 隐藏层使用ReLU激活函数
return self.fc2(x)
class DQN:
''' DQN算法 '''
def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma,
epsilon, target_update, device):
self.action_dim = action_dim
self.q_net = Qnet(state_dim, hidden_dim,
self.action_dim).to(device) # Q网络
# 目标网络
self.target_q_net = Qnet(state_dim, hidden_dim,
self.action_dim).to(device)
# 使用Adam优化器
self.optimizer = torch.optim.Adam(self.q_net.parameters(),
lr=learning_rate)
self.gamma = gamma # 折扣因子
self.epsilon = epsilon # epsilon-贪婪策略
self.target_update = target_update # 目标网络更新频率
self.count = 0 # 计数器,记录更新次数
self.device = device
def take_action(self, state): # epsilon-贪婪策略采取动作
if np.random.random() < self.epsilon:
action = np.random.randint(self.action_dim)
else:
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.q_net(state).argmax().item()
return action
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'],
dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
self.device)
rewards = torch.tensor(transition_dict['rewards'],
dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'],
dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'],
dtype=torch.float).view(-1, 1).to(self.device)
q_values = self.q_net(states).gather(1, actions) # Q值
# 下个状态的最大Q值
max_next_q_values = self.target_q_net(next_states).max(1)[0].view(
-1, 1)
q_targets = rewards + self.gamma * max_next_q_values * (1 - dones
) # TD误差目标
dqn_loss = torch.mean(F.mse_loss(q_values, q_targets)) # 均方误差损失函数
self.optimizer.zero_grad() # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
dqn_loss.backward() # 反向传播更新参数
self.optimizer.step()
if self.count % self.target_update == 0:
self.target_q_net.load_state_dict(
self.q_net.state_dict()) # 更新目标网络
self.count += 1
2.3 训练画图
lr = 2e-3
num_episodes = 500
hidden_dim = 128
gamma = 0.98
epsilon = 0.01
target_update = 10
buffer_size = 10000
minimal_size = 500
batch_size = 64
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
"cpu")
env_name = 'CartPole-v0'
env = gym.make(env_name)
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = ReplayBuffer(buffer_size)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon,
target_update, device)
return_list = []
for i in range(10):
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)):
episode_return = 0
state = env.reset()
done = False
while not done:
action = agent.take_action(state)
next_state, reward, done, _ = env.step(action)
replay_buffer.add(state, action, reward, next_state, done)
state = next_state
episode_return += reward
# 当buffer数据的数量超过一定值后,才进行Q网络训练
if replay_buffer.size() > minimal_size:
b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
transition_dict = {
'states': b_s,
'actions': b_a,
'next_states': b_ns,
'rewards': b_r,
'dones': b_d
}
agent.update(transition_dict)
return_list.append(episode_return)
if (i_episode + 1) % 10 == 0:
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(env_name))
plt.show()
总结
提示:这里对文章进行总结:
本章讲解了 DQN 算法,其主要思想是用一个神经网络来表示最优策略的函数,然后利用 Q-learning 的思想进行参数更新。为了保证训练的稳定性和高效性,DQN 算法引入了经验回放和目标网络两大模块,使得算法在实际应用时能够取得更好的效果。在 2013 年的 NIPS 深度学习研讨会上,DeepMind 公司的研究团队发表了 DQN 论文,首次展示了这一直接通过卷积神经网络接受像素输入来玩转各种雅达利(Atari)游戏的强化学习算法,由此拉开了深度强化学习的序幕。