算法图解里面的代码是什么代码啊_一文带你理清DDPG算法（附代码及代码解释）...

DDPG，全称是deep deterministic policy gradient，深度确定性策略梯度算法。

deep很好理解，就是用深度网络。policy gradient我们也学过了。

那什么叫deterministic确定性呢？其实DDPG也是解决连续控制型问题的的一个算法，不过和PPO不一样，PPO输出的是一个策略，也就是一个概率分布，而DDPG输出的直接是一个动作。

DDPG和PPO一样，也是AC的架构。加上名字上有PG字眼，所以在学习的时候，很多人会以为DDPG就是只输出一个动作的PPO，所以直接省去了impotance sampling等一堆麻烦的事情。

但个人认为，两者的思路是完全不一样的，DDPG更接近DQN，是用一个actor去弥补DQN不能处理连续控制性问题的缺点。

这一点要非常注意，是非常容易混淆的一点。

如果你对DQN还不太了解，请一下这两篇关于DQN的专栏：

张斯俊：三维可视化助你直观理解DQN算法[DQN理论篇]​zhuanlan.zhihu.com

张斯俊：用可视化直观理解DQN[DQN实战篇]​zhuanlan.zhihu.com

DDPG 和 DQN

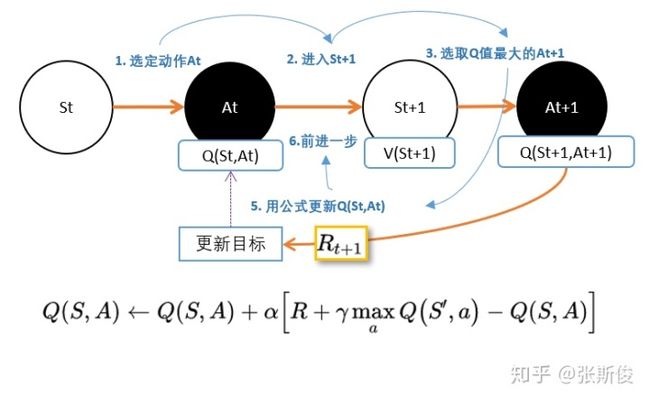
我们先来回顾DQN。DQN是更新的动作的q值：

我们从公式中也能看出，DQN不能用于连续控制问题原因，是因为maxQ(s',a')函数只能处理离散型的。那怎么办？

我们知道DQN用magic函数，也就是神经网络解决了Qlearning不能解决的连续状态空间问题。那我们同样的DDPG就是用magic解决DQN不能解决的连续控制型问题就好了。

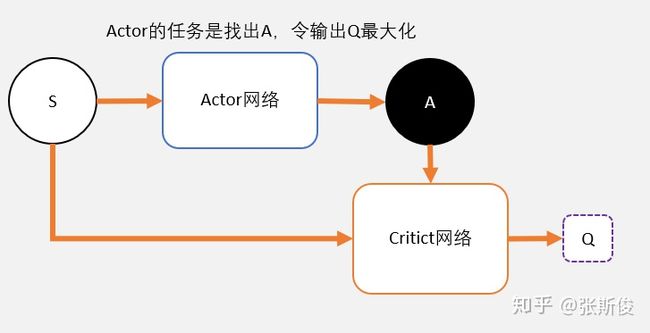
也就是说，用一个magic函数，直接替代maxQ(s',a')的功能。也就是说，我们期待我们输入状态s，magic函数返回我们动作action的取值，这个取值能够让q值最大。这个就是DDPG中的Actor的功能。

我们可以这样形象地理解DDPG。

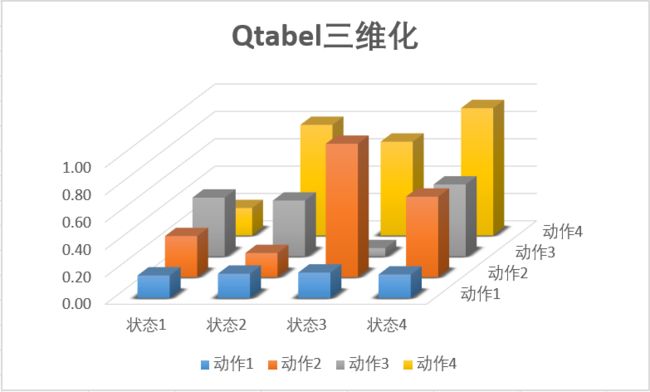
我们之前讲DQN也说过，DQN的深度网络，就像用一张布去覆盖Qlearning中的Qtable。这也是DDPG中Critic的功能。

示意图：

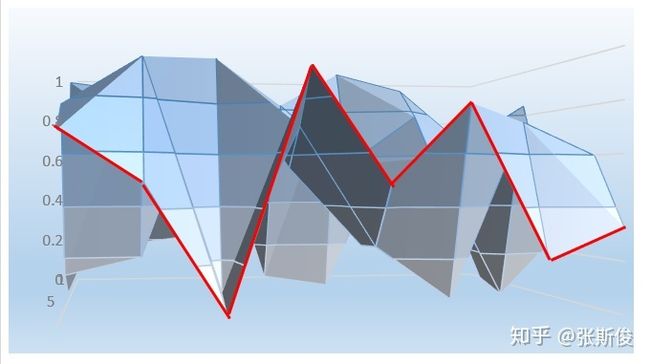
当我们把某个state输入到DDPG的Actor中的时候，相当于在这块布上做沿着state所在的位置剪开，这个时候大家会看到这个边缘是一条曲线。

如上图中的红色曲线，这条曲线很像概率分布，但要一定注意，这里并不是策略，也不是PPO和AC中的V值。

是在某个状态下，选择某个动作值的时候，能获得的Q值。

Actor的任务就是在寻找这个曲线的最高点，然后返回能获得这个最高点，也是最大Q值的动作。

所以，DDPG其实并不是PG，并没有做带权重的梯度更新。而是在梯度上升，在寻找最大值。

这也就解释了，为什么DDPG是一个离线策略，但可以多次更新却不用importance sampling。这是因为这个算法就是DQN，和策略没有直接的关系。

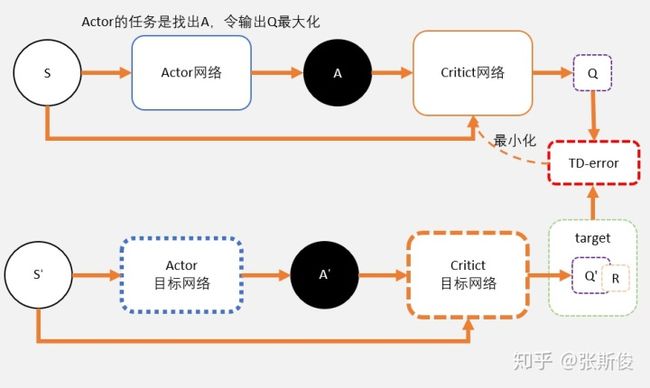
DDPG算法

我们现在整理：

Critic

• Critic网络的作用是预估Q，虽然它还叫Critic，但和AC中的Critic不一样，这里预估的是Q不是V；
• 注意Critic的输入有两个：动作和状态，需要一起输入到Critic中；
• Critic网络的loss其还是和AC一样，用的是TD-error。这里就不详细说明了，我详细大家学习了那么久，也知道为什么了。

Actor

• 和AC不同，Actor输出的是一个动作；
• Actor的功能是，输出一个动作A，这个动作A输入到Crititc后，能够获得最大的Q值。
• 所以Actor的更新方式和AC不同，不是用带权重梯度更新，而是用梯度上升。

弄清楚怎么来的，就不会和PPO混淆在一起了。也就明白为什么说DDPG是源于DQN而不是AC了。

所以，和DQN一样，更新的时候如果更新目标在不断变动，会造成更新困难。所以DDPG和DQN一样，用了固定网络(fix network)技术，就是先冻结住用来求target的网络。在更新之后，再把参数赋值到target网络。

所以在实做的时候，我们需要4个网络。actor, critic, Actor_target, cirtic_target。

有的同学会搞混几个网络到底怎么用。其实只要记着一点：目标网络只是用在求target的过程中。如果不是求target用的，就不用目标网络。

示例代码

这一篇，我们以tensorflow给出的强化学习算法示例代码为例子，看看DDPG应该如何实现。

https://github.com/tensorlayer/tensorlayer/blob/master/examples/reinforcement_learning/tutorial_DDPG.py​github.com

如果一时间看代码有困难，可以看我的带注释版本。希望能帮助到你。

https://github.com/louisnino/RLcode/blob/master/tutorial_DDPG.py​github.com

神经网络

现在我们先看看actor的建立。

def get_actor(input_state_shape, name=''):
     inputs = tl.layers.Input(input_state_shape, name='A_input')
     x = tl.layers.Dense(n_units=30, act=tf.nn.relu, W_init=W_init, b_init=b_init, name='A_l1')(inputs)
     x = tl.layers.Dense(n_units=a_dim, act=tf.nn.tanh, W_init=W_init, b_init=b_init, name='A_a')(x)
     x = tl.layers.Lambda(lambda x: np.array(a_bound) * x)(x) 
     return tl.models.Model(inputs=inputs, outputs=x, name='Actor' + name)

我们需要留意，actor最终输出的action有一定的范围，这个范围在环境中已经定义好。

我们可以用语句获取动作空间的取值范围: a_bound = env.action_space.high #action取值范围上限 a_bound = env.action_space.low #action取值范围下限

超过范围的action可能会导致程序异常。一种比较好的处理方式是，在网络末端，用tanh函数，把输出映射到[-1.0,1.0]之间。

然后通过Lamda层的lambda表达式，例如示例代码中：np.array(a_bound) * x ，把动作从[-1.0,1.0]映射到环境需要的取值范围。

Critic网络

def get_critic(input_state_shape, input_action_shape, name=''):
     s = tl.layers.Input(input_state_shape, name='C_s_input')
     a = tl.layers.Input(input_action_shape, name='C_a_input')
     x = tl.layers.Concat(1)([s, a])
     x = tl.layers.Dense(n_units=60, act=tf.nn.relu, W_init=W_init, b_init=b_init, name='C_l1')(x)
     x = tl.layers.Dense(n_units=1, W_init=W_init, b_init=b_init, name='C_out')(x)
     return tl.models.Model(inputs=[s, a], outputs=x, name='Critic' + name)

Critic和DQN有些许不同，在DQN，我们会计算Q(s)，把该state下的所有动作的q值都输出，然后从中挑选q值最大的一个动作。

而在DDPG，我们会把动作a也输出到network，由network去评判这个action的q值。所以我们需要把a和s一起放入到Critic中去。Q(s,a)

1. 我们定义两个输入层，如示例代码中的s，a。
2. 这两层会同时输入到下一层，所以我们用Concat层，把s，a的输出叠加起来，再输入到下一层。
3. 最后我们记得在模型的input定义中输入两个输入：inputs=[s, a]即可。

主流程

for i in range(MAX_EPISODES):
    s = env.reset()
    for j in range(MAX_EP_STEPS):
        a = ddpg.choose_action(s) 
        a = np.clip(np.random.normal(a, VAR), -2, 2) 
        s_, r, done, info = env.step(a)
        ddpg.store_transition(s, a, r / 10, s_)
        if ddpg.pointer > MEMORY_CAPACITY:
              ddpg.learn()
         s = s_ 

我们把示例代码整理一下，可以获得以上的代码框架。我们说过，DDPG来源于DQN，是一种离线的算法。所以DDPG和DQN的更新流程几乎一样。

1. 重置状态s
2. 选择动作a
3. 与环境互动，获得 s_, r, done 数据
4. 保存数据
5. 如果数据量足够，就对数据进行随机抽样，更新Actor和Critic
6. 把s_赋值给s，开始新的一步

a = ddpg.choose_action(s) 
        a = np.clip(np.random.normal(a, VAR), -2, 2) 

其中，我们重点关注这两行代码。

我们先看ddpg.choose_action(s)，ddpg.choose_action(s)的功能很简单，就是把s整理一下，放入Actor网络，输出action。

但如何保证选出来的动作有足够的随机性，能够充分探索环境呢？DQN采用的是epsilon-greedy的算法。而DDPG用了正态分布抽样方式。

我们用输出的a作为一个正态分布的平均值，加上参数VAR，构造一个正态分布。然后从正态分布中随机出一个新的动作代替a。我们知道a作为正态分布的均值，也是一个有最大概率获得的一个值。这就有点像epsilon-greedy，有一定概率在探索，也有一定概率在开发新的动作。

我们可以用VAR来控制探索的程度： VAR越小，正态分布形状越“瘦”，选择a的概率会更大，开发的性质更多； VAR越大，正态分布形状越“胖”，选择a的概率会更小，探索的性质更多；

我们还可以动态控制VAR的大小，例如经过N轮的更新，就updata VAR，让智能体的开发行为更多一点。

值得注意的是，在训练好智能体之后，我们就不要再做探索了，把第二行代码去掉，直接用Actor输出的动作就可以了。

智能体学习

现在我们看learning函数。我把leaning函数分为三部分。我们先看第一部分，数据抽样。

#随机BATCH_SIZE个随机数
        #1
        indices = np.random.choice(MEMORY_CAPACITY, size=BATCH_SIZE)    
        #2
        bt = self.memory[indices, :]                         #根据indices，选取数据bt，相当于随机
        #3
        bs = bt[:, :self.s_dim]                                 #从bt获得数据s
        ba = bt[:, self.s_dim:self.s_dim + self.a_dim]    #从bt获得数据a
        br = bt[:, -self.s_dim - 1:-self.s_dim]              #从bt获得数据r
        bs_ = bt[:, -self.s_dim:]                               #从bt获得数据s'

我们之前学习过几种存储方式，其实都是大同小异的。大家可以用自己喜欢的方式。在示例代码中，作者直接用了一个矩阵，保存所有的数据。需要用的时候，再进行切分。

# 创建初始化memory
self.memory = np.zeros((MEMORY_CAPACITY, s_dim * 2 + a_dim + 1), dtype=np.float32)

1. 当我们要提取的时候，首先随机抽取一定的行号所谓索引（indices），例如batch个。
2. 把这些数据抽出来
3. 根据保存的顺序，把数据切割，恢复成bs，ba，br，bs_

Critic更新

with tf.GradientTape() as tape:
      a_ = self.actor_target(bs_)
      q_ = self.critic_target([bs_, a_])
      y = br + GAMMA * q_
      q = self.critic([bs, ba])
      td_error = tf.losses.mean_squared_error(y, q)
   c_grads = tape.gradient(td_error, self.critic.trainable_weights)
   self.critic_opt.apply_gradients(zip(c_grads, self.critic.trainable_weights))

Critic的更新原理和DQN是一样的。但在计算更新目标y的时候，记得用上target_net.

Actor更新

        with tf.GradientTape() as tape:
            a = self.actor(bs)
            q = self.critic([bs, a])
            a_loss = -tf.reduce_mean(q)  
        a_grads = tape.gradient(a_loss, self.actor.trainable_weights)
        self.actor_opt.apply_gradients(zip(a_grads, self.actor.trainable_weights))

在这里我们要注意，a_loss = -tf.reduce_mean(q) 前面的负号。这是和AC最大的不同之处。

在AC采用的是加权梯度方法，权重的方向，代表了更新的方向；权重越大，更新程度越大。

DDPG采用的是梯度上升的方法。可以理解为尝试去找一个最大值。由于和梯度下降方向相反，我们需要在loss加一个负号。

滑动平均值更新

按照DQN的方式，我们需要把更新后的参数赋值给target network的参数。我们称这种更新为“硬更新”。在示例代码中，采用了另外一种更新方式，“滑动平均值更新”。

滑动平均值的计算原理也并不复杂：新加入的元素 和 旧的平均值 以一定比例混合成新的平均值。当然，这两者比例加起来会等于1.

新的平均值 = 旧的平均值 * 比例 + 新加入元素 * 比例

我们观察表格，就能发现移动平均值的特点： 1.虽然移动平均值和真实平均值有一定差距，但在新元素和旧平均值相差不大的情况下，是趋于均值的。 2.不需要保存所有的元素，也不需要保存元素个数，只需要保存一个旧均值就可以了。这个旧均值有时候我们会称为影子。 3.即使有个别元素比较大，对均值的影响还是比较“温和”的。不会造成巨大的跳变。

第三点是我们最想要的性质。我们之前说过，我们需要targetnetwork的原因，是不希望在更新的同时，目标也同时移动，这相当于在打“移动靶”。所以我们把靶子固定住，这样我们就可以减少更新的难度。

但如果我们采用硬更新的方式，每次靶子出现的地方都相差很远。这同样不利于我们更新。所以我们限制一下前后两个靶的差距，希望不要造成巨大的跳变。这也更新起来就更顺畅了。

示例代码中，滑动平均值的计算直接用tensorflow的工具.ExponentialMovingAverage。

其中decay就是比例。我们用TAU表示新加入元素的混合比例。1-TAU，就是旧平均值的比例。

        #建立ema，滑动平均值
        self.ema = tf.train.ExponentialMovingAverage(decay=1 - TAU)  # soft replacement
    def ema_update(self):
        #1
        paras = self.actor.trainable_weights + self.critic.trainable_weights    #获取要更新的参数
        self.ema.apply(paras)   
        #2
        for i, j in zip(self.actor_target.trainable_weights + self.critic_target.trainable_weights, paras):
            i.assign(self.ema.average(j))   # 用滑动平均赋值

1. 使用的时候，我们先要确定我们要更新的变量，并使用apply，添加相应影子（旧均值）副本。
2. 和硬更新一样，我们把变量一一对应并更新，但在更新之前，先计算滑动均值，再赋值到target。

个人觉得，tensorflow自带的工具虽然方便，但其实不利于理解，对于初学者来说会感觉有"神秘"。其实在下一章TD3中也用到了滑动平均值更新这项技术。但代码更简明。

代码中，除了先计算滑动平均值外，其余代码其实和硬更新是一样的。

    def target_soft_update(self, net, target_net, soft_tau):
        ''' soft update the target net with Polyak averaging '''
        for target_param, param in zip(target_net.trainable_weights, net.trainable_weights):
            target_param.assign(  # copy weight value into target parameters
                target_param * (1.0 - soft_tau) + param * soft_tau
                #  旧的平均值 * (1 - 新元素比例) + 新加入元素 * 新元素比例
            )
        return target_net

总结

现在我们来总结一下 1. DDPG源于DQN，而不是源于AC。这一点要搞清楚。 2. Actor用的是梯度上升，而不是带权重的梯度更新； 3. 虽然Critic和AC一样，都是用td-error来更新；但AC的critic预估的是V，DDPG预估的是Q

好了，在下一篇，我们会进入TD3，就是DDPG的进化版。但如果你已经理解了DDPG，那么TD3也很容易理解了。下篇见。

如果专栏对你有用，请点赞并关注在下喔。如果发现有问题，也可以在文章下留言。

你的每一点关注，都是在下的继续努力的动力来源！感激！

白话强化学习​zhuanlan.zhihu.com