学习笔记 | TNNLS 2022 THPs:学习事件序列因果结构的拓扑霍克斯过程
文章目录
- 一、序言
- 二、Introduction
- 三、Related Work
- 四、拓扑霍克斯过程
- 五、总结
CSDN 叶庭云:https://yetingyun.blog.csdn.net/
一、序言
THPs: Topological Hawkes Processes for Learning Causal Structure on Event Sequences
论文地址:https://ieeexplore.ieee.org/document/9781798

作者:蔡瑞初、吴思宇、乔杰、郝志峰、张可力 等
代码地址:gCastle 里封装的算法
关键词:因果结构学习、事件序列、拓扑霍克斯过程(THPs)
在多类型事件序列上学习事件类型之间的因果结构是一项重要但非常具有挑战性的任务。现有方法,例如多元霍克斯过程,大多假设每个序列都是独立同分布的。然而,在许多实际应用中,经常遇到隐藏在事件序列背后的拓扑网络,使得事件不仅被其历史激发或抑制,而且被其拓扑邻居激发或抑制。因此,未能有效描述事件序列之间的拓扑依赖性可能会导致因果结构的错误检测。通过从时间卷积的角度考虑霍克斯过程,作者提出了拓扑霍克斯过程(THP),以在拓扑域中的图卷积与时域中的时间卷积之间建立联系。并进一步在 likelihood 框架中提出了一种关于 THPs 的因果结构学习方法。所提出的方法具有基于图卷积的 THP 似然函数和具有似然函数期望最大化的稀疏优化方案。对合成数据和真实数据的理论分析和实验证明了所提出方法的有效性。
二、Introduction
在许多现实世界应用中,学习多类型事件序列上事件类型之间的因果结构是一项重要任务。例如,社会科学家可能对研究社会事件之间的因果关系感兴趣,经济学家可能对分析经济时间序列之间的因果关系感兴趣,网络运维工程师试图定位集中发生的报警事件的根本原因。已经提出了各种方法来发现多类型事件序列的因果关系。一是基于约束(constraint-based)的方法,重点是探索因果变量内的独立性。典型的方法包括 PC 以及瞬时条件独立性(PCMCI)测试,以及基于传递熵的方法。另一条线是基于点过程的方法,重点是对事件的产生过程进行建模。典型的方法包括基于多元霍克斯过程的方法,作者的工作属于基于多元霍克斯过程的方法。
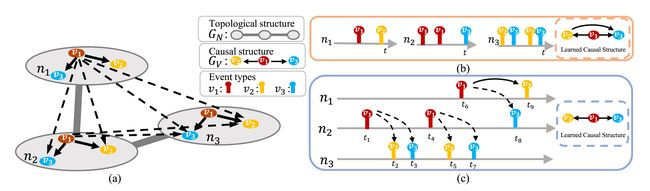
这些现有方法的一个共同假设是事件序列是独立同分布的 (IID)。然而,在许多现实世界的场景中,事件序列通常由拓扑网络中的节点生成,这样一个事件不仅会被序列内的事件激发或抑制,还会被其拓扑邻居中的事件激发或抑制。例如,考虑下图中给出的移动网络,有 3 种类型的警报 v 1 、 v 2 、 v 3 v_{1}、v_{2}、v_{3} v1、v2、v3 传播到具有因果结构 G V \mathcal{G}_{V} GV 的网络站点 G N \mathcal{G}_{N} GN。人们希望确定警报类型之间的因果关系,以帮助操作和维护移动网络。这里,每个节点代表移动网络中的一个网元,节点之间的边代表一条物理连接。
此外,在这种情况下,节点 n 1 、 n 2 、 n 3 n_{1}、n_{2}、n_{3} n1、n2、n3 产生的报警事件序列不再独立,因为级联故障将通过每个网元之间的物理连接从一个节点到另一个节点发生。即故障告警类型 v 1 → v 2 v_{1} \rightarrow v_{2} v1→v2 的因果关系也会出现在邻居之间(虚线)。然后,如果我们忽略隐藏在事件序列背后的拓扑结构,独立地处理不同节点的序列,则现有方法可能会引入不可观察的混杂,并返回脆弱和不稳定的结果。如图(b)所示,如果我们忽略拓扑信息并对序列进行独立处理,事实证明这将建立一个错误发现的因果关系 v 2 → v 3 v_{2} \rightarrow v_{3} v2→v3。具体来说,在 IID 假设下,对于 n 3 n_{3} n3 中的 v 2 v_{2} v2 和 v 3 v_{3} v3, n 2 n_{2} n2 中的 v 1 v_{1} v1 变为不可观察的混杂因素,导致错误检测 v 2 v_{2} v2 和 v 3 v_{3} v3 之间强依赖性。在很多场景中也可以发现这样的现象。例如,在社会科学中,个体的行为可能通过社会网络(人际关系的拓扑结构)以某种方式相互影响。
因此,考虑数据背后的拓扑结构对于学习因果结构至关重要。 然而,由于因果影响的复杂传播,拓扑信息的有效建模是一项非平凡的任务。
为了填补这一空白,作者将霍克斯过程的时域卷积特性扩展到 Time-Graph 域以有效解决拓扑依赖性问题,并进而提出了拓扑霍克斯过程(THPs)。在这样的过程中,事件的生成过程受到拓扑结构 G N \mathcal{G}_{N} GN 和因果结构 G V \mathcal{G}_{V} GV 的联合约束,如图(c)所示。进一步使用时间卷积和图卷积推导了 THPs 的似然函数,这种似然模型通过基于期望最大化(Expectation-Maximization)的稀疏优化方案进行优化。
三、Related Work
Point Processes(点过程)。近期研究中针对复杂事件序列的点过程主要有两类:
- 第一种是霍克斯过程,它假设历史事件对未来事件有影响。它使用参数或非参数强度函数来模拟一维和多维情况中点过程的自激和互激机制。
- 第二类点处理是基于 Deep Learning 的点过程方法,它使用可学习的强度函数来捕获从过去到将来的非线性影响。虽然几何 Hawkes 过程(GHPs)使用图卷积网络来建模自激式 Hawkes 过程参数之间的关系,但它并没有对多元过程之间的依赖性进行建模。
格兰杰因果关系
- 为了学习事件类型之间的格兰杰因果关系,提出了基于 Hawkes 过程的多元 Hawkes 过程。
- 这些方法的变体主要集中在正则化和强度函数的设计上。例如,乘法器和主要化最小化的交替方向方法(ADM4)使用核和 L1 范数作为稀疏正则化项,最大似然估计与 sparse-group-lasso(MLE-SGL)进一步考虑时间稀疏性和成对相似性正则化,以及非参数霍克斯累积量(NPHC)提出了一种新的非参数方法来估计多元霍克斯过程的集成核矩阵。最近,还提出了一些基于深度点过程的方法。例如,循环点过程网络(RPPNs)引入了注意力机制来保留事件的准因果关系,事件顺序归因的因果关系(CAUSEs)使用归因方法结合深度神经网络学习格兰杰因果关系。
- 作者的工作还与 Proximal Graphical Event Model(PGEM) 有关,该模型使用贪婪算法搜索因果图,但假设事件类型仅取决于具有固定窗口大小的最近历史记录。一些工作还考虑了非独立同分布下学习点过程。例如,引入了一阶和二阶属性来表征霍克斯过程,提出在异构数据下学习有向信息图,但它们都没有考虑数据背后的拓扑图。除了基于点过程的方法外,还提出了一些方法,通过使用传递熵从事件序列中非参数化地学习格兰杰因果关系。
准备知识:多元点过程(Multivariate Point Processes)、图卷积(Graph Convolution)、
四、拓扑霍克斯过程
在这项工作中,作者考虑了现实世界的场景,即事件序列通常由拓扑网络中的节点生成,这样一个事件不仅会被序列本身发生的因果事件激发或抑制,还会被其在拓扑邻居中的因果事件激发或抑制。为了正式化上述场景,作者使用无向图 G N = ( N , E N ) \mathcal{G}_{N}=\left(\mathbf{N}, \ \mathbf{E}_{N}\right) GN=(N, EN) 表示节点 N \mathbf{N} N 构成的拓扑图,一个有向图 G V = ( V , E V ) \mathcal{G}_{V}=\left(\mathbf{V},\ \mathbf{E}_{V}\right) GV=(V, EV) 表示事件类型之间的因果结构 V \mathbf{V} V。其中 E N \mathbf{E}_{N} EN 和 E V \mathbf{E}_{V} EV 分别表示拓扑图和因果图中的边集。基于以上符号,进一步扩展传统的事件序列 E = { v i , t i } i = 1 m \mathcal{E}=\left\{v_{i},\ t_{i}\right\}_{i=1}^{m} E={vi, ti}i=1m 为 E = { n i , v i , t i } i = 1 m \mathcal{E}=\left\{n_{i},\ v_{i},\ t_{i}\right\}_{i=1}^{m} E={ni, vi, ti}i=1m,通过利用 n i ∈ N n_{i} \in \mathbf{N} ni∈N 在拓扑图中表示相应的节点。
学习拓扑事件序列的因果结构:给定一组观察到的事件序列 E = { n i , v i , t i } i = 1 m , n i ∈ N , v i ∈ V , t i ∈ T \mathcal{E}=\left\{n_{i},\ v_{i},\ t_{i}\right\}_{i=1}^{m}, \ n_{i} \in \mathbf{N}, \ v_{i} \in \mathbf{V}, \ t_{i} \in \mathbf{T} E={ni, vi, ti}i=1m, ni∈N, vi∈V, ti∈T 以及它们对应的拓扑图 G N \mathcal{G}_{N} GN,这项工作的目标是发现事件类型 V \mathbf{V} V 之间的因果结构 G V \mathcal{G}_{V} GV。
不难看出,现有的多元霍克斯过程对于上述问题是有限的。因为现有的多元霍克斯过程假设序列的集合是 IID 的,并且忽略数据生成过程背后的底层拓扑结构,这可能导致如图(b)中所述的错误检测。因此,通过将拓扑图引入霍克斯过程,作者提出了 THP 来处理拓扑事件序列。然而,将拓扑图引入霍克斯过程是一项不平凡的任务,因为一个事件可能会被其拓扑邻居通过不同路径的因果事件激发或抑制。这种观察意味着事件类型的强度可以被视为不同路径上因果事件类型强度的总和,这启发了一种使用图卷积对其建模的方法。
将图卷积引入多元霍克斯过程,从传统霍克斯过程的时间卷积视角开始推导,发现霍克斯过程的强度函数本质上是时域的卷积运算,这意味着强度函数是过去所有因果相关事件在时间 t t t 的累积效应。实际上,通过假设拓扑图在时间上的不变性,推导出的联合卷积运算可以分解为两部分。
推导拓扑霍克斯过程的似然。基于前面的理论分析,知道约束稀疏性对于获得合理的因果结构至关重要。因此,作者在似然框架下使用贝叶斯信息准则(BIC)分数设计了具有稀疏约束的目标函数。
似然的稀疏优化。虽然已经针对稀疏问题提出了各种方法,例如,ADM4 方法在因果图上使用低秩约束,MLE-SGL 方法进一步引入了 sparse-group-lasso 正则化,它们的性能仍然在很大程度上取决于稀疏正则化强度的选择或修剪以前未知的结构的阈值。为了解决这个问题,作者分两步提出了稀疏优化方案,这样估计和优化步骤就会迭代进行,以强制学习稀疏因果结构。为了学习最佳因果图,提出了一种爬山算法来搜索具有最高支持的最佳 s u p Θ L B ( G V , Θ ; X , G N ) sup_{\Theta} \ L_{B}\left(\mathcal{G}_{V}, \Theta ; \mathbf{X}, \mathcal{G}_{N}\right) supΘ LB(GV,Θ;X,GN) 的 G V \mathcal{G}_{V} GV,由上述 EM 算法(算法 1 的第 7 行)优化。
对合成数据和真实数据的理论分析和实验证明了所提出方法的有效性。
五、总结
在这项工作中,作者提出了一个拓扑霍克斯过程来学习多元事件序列的因果结构。通过将时域卷积扩展到 Graph-Time 域联合卷积,该模型在统一的似然框架中同时采用拓扑约束和因果约束,成功找到不同事件类型之间的因果结构。据作者所知,这是目前第一个针对具有拓扑约束的事件序列的因果结构学习方法。THPs 的成功不仅为现实世界的事件序列提供了有效的解决方案,而且为非独立同分布的因果发现指明了一个有前途的方向。将来,作者计划将工作扩展到具有更通用的图卷积核的通用点过程。
论文的主要贡献如下:
- 为拓扑网络生成的事件序列提出 THPs;
- 使用 Graph-Time 域上的联合卷积推导 THP 的似然函数;
- 并为上述似然函数开发有效的稀疏优化模式;
- 对所提出的模型进行理论分析和广泛的实验,对合成数据和真实数据的理论分析和进行大量实验证明了所提出方法的有效性。
补充学习:
- PCIC 2021 | 华为诺亚方舟 & 北京大学因果推理挑战赛
- 梦家博客 | 因果推理之霍克斯过程 Hawkes process
- Causal Discovery in Hawkes Processesby Minimum Description Length
- 集智俱乐部 | 因果发现最新进展及其在电信网络运营维护的实践探讨
- 以机器学习的视角来看时序点过程的最新进展