离散选择模型之Gumbel分布

离散选择模型有用链接：https://eml.berkeley.edu/books/choice2.html

Gumbel 分布

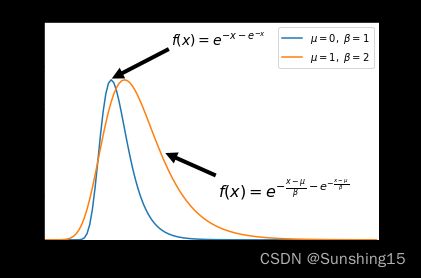
Gumbel分布是一种极值型分布, 其概率密度分布函数为
$$f(x;\mu ,\beta )=e^{-z-e^{-z}},z=\frac{x-\mu }{\beta }$$,其中 $\mu$ 为位置系数 （Gumbel分布的众数是 $\mu$）; $\beta$ 为尺度系数 (Gumbel分布的方差为 $\frac{{\pi }^2}{6}{\beta }^2$)
标准Gumbel分布，$\mu =0$, $\beta =1$
概率密度分布函数为
$$f(x;\mu ,\beta )=e^{-x-e^{-x}}$$
Python Gumbel概率密度函数代码

import numpy as np
import matplotlib.pyplot as plt
def gumbel_pdf(x, mu=0, beta=1):
    z = (x - mu) / beta
    y = np.exp(-z - np.exp(-z))
    return y
######## 分布函数##############
def gumbel_cdf(x, mu=0, beta=1):
    z = (x - mu) / beta
    y = np.exp(- np.exp(-z))
    return y
################################


x = np.arange(-5., 20, 0.2)
plt.plot(x,gumbel_pdf(x, 0, 1),label= r'$\mu=0,\ \beta=1$')
plt.plot(x,gumbel_pdf(x, 1, 2),label= r'$\mu=1,\ \beta=2$')
plt.axis([-5, 20, 0, 0.4])
plt.ylim([0, 0.5])
plt.xlabel('$x$')
plt.ylabel('Probability')
plt.title('Standard Gumbel distribution probability density distribution curve')
plt.legend(loc='best')
plt.annotate(r'$f(x)=e^{-x-e^{-x}}$',xy=(0, 0.37), xytext=(4.5, 0.45),
             arrowprops=dict(facecolor='black', shrink=0.01,linewidth=0.01),fontsize=14
             )
plt.annotate(r'$f(x)=e^{-\frac{x-\mu}{\beta}-e^{-\frac{x-\mu}{\beta}}}$',xy=(4, 0.2), xytext=(8, 0.1),
             arrowprops=dict(facecolor='black', shrink=0.01,linewidth=0.01),fontsize=16
             )
plt.show()

图片展示

若随机变量 $\xi$ 服从标准Gumbel分布，则其期望为
$$\mathbb{E}(\xi )={\int }_{-\infty }^{+\infty }x{e}^{-x-e^{-x}}dx=-r$$方差为$$\mathbb{D}(\xi )={\int }_{-\infty }^{+\infty }{x}^2{e}^{-x-e^{-x}}dx=\frac{{\pi }^2}{6}$$其中$r$ 为 Euler 常数，$r=0.577215$
累积概率密度函数公式为
$$F(x;\mu ,\beta )=e^{-e^{-\frac{x-\mu }{\beta }}}$$

matlab 产生服从极值分布的相关函数

I类型极值分布（Gumbel分布）

若随机量 $x$ 服从威布尔分布（Weibull distribution），那么 $X=log(x)$ 服从I类型极值分布

1. evrnd() 生成极值分布随机数，默认生成服从极小值极值分布（即Gumbel分布）
   语法

R = evrnd(mu, sigma)%产生位置参数为mu，尺度参数为sigma的随机数
R = evrnd(mu, sigma, m, n,...)
R = evrnd(mu, sigma, [m, n, ...])

2. evpdf(x, mu, sigma) 返回I类型位置参数为mu，尺度参数为sigma在x点处的极值分布的概率密度函数值

3. evcdf()用于表示极值累积分布函数

p = evcdf(x,mu,sigma)
[p, plo, pup] = evcdf(x, mu, sigma, pcov, alpha)
[p, plo, pup] = evcdf(x, mu,sigma, pcov, alpha, 'upper')

• p = evcdf(x,mu,sigma)返回I类型位置参数为mu，尺度参数为sigma在x点处的极值分布的累积概率值
• [p, plo, pup] = evcdf(x, mu, sigma, pcov, alpha)返回I类型位置参数为mu，尺度参数为sigma在x点处的极值分布的累积概率值的置信区间域，plo和pup分别为置信区间域的上界和下界
• [p, plo, pup] = evcdf(x, mu,sigma, pcov, alpha, ‘upper’)使用一种更精确地计算上尾概率的算法返回I类型位置参数为mu，尺度参数为sigma在x点处的极值分布的累积概率值的置信区间域，plo和pup分别为置信区间域的上界和下界

4. evfit() 用于极值参数估计
   语法

parmhat = evfit(data)
[parmhat,parmci] = evfit(data)
[parmhat,parmci] = evfit(data,alpha)
[...] = evfit(data,alpha,censoring)
[...] = evfit(data,alpha,censoring,freq)
[...] = evfit(data,alpha,censoring,freq,options)

• parmhat = evfit(data)估计给定样本数据data的服从I类极值分布时的极大似然估计参数值。样本数据必须为双精度的向量，返回值为I类极值分布的位置参数mu与尺度参数sigma
• [parmhat,parmci] = evfit(data) 估计给定样本数据data服从I类极值分布时的极大似然估计参数值，以及95%置信区间的估计值的置信区间。其中parmci代表估计参数值的位置参数mu与尺度参数sigma的区间，第一列为位置参数区间，第二列为尺度参数区间。如

[parmhat,parmci] = evfit([1,2,3,4,5,6,7,8])
parmhat =
    5.6400    2.0647
parmci =
    4.1251    1.2050
    7.1549    3.5379

• [parmhat,parmci] = evfit(data,alpha)功能同上，不同之处在于可以自行指定置信度。这里的alpha为区间[0,1]范围内的一个数用于制定执行区间的宽度。默认值为0.05.
• [parmhat,parmci] = evfit(data,alpha,censoring)。此处censoring为同样本数据data同维度的布尔矢量，用于标注数据的删失情况。其中1代表数据值是右删失的，0代表数据值为精确观测值。如

[parmhat,parmci] = evfit([1,2,3,4,5,6,7,8],0.05,[1,0,1,0,1,0,1,0])
parmhat =
 7.0141    1.7707
parmci =
 5.2695    0.8435
 8.7588    3.7173

• [parmhat,parmci] = evfit(data,alpha,censoring,freq)接受一个频率向量。其中freq和样本数据具有相同的维度。通常，频率向量包含数据中相应元素的整数频率，但是频率向量中可为任何非负值。
• [parmhat,parmci] = evfit(data,alpha,censoring,freq, option)可指定选项进行输出。option使用函数statset, 可在matlab控制台help statset

5. evinv() 用于计算已知概率值下的样本值

语法

X = evinv(P,mu,sigma)
[X,XLO,XUP] = evinv(P,mu,sigma,pcov,alpha)

6. evlike() 用于计算极值负对数似然值。 matlab help evlike

7. [M,V] = evstat(mu,sigma)返回位置参数为mu尺度参数为sigma的Gumbel分布的均值与方差。

广义极值分布

设 $X_1,X_2,\dots ,X_n$ 为独立同分布的随机变量样本数据，$$M_n=max\{X_1,X_2,\dots ,X_n\}$$表示这$n$ 个随机变量样本的最大值，则 $M_n$ 服从某种极值分布。Gnedenko证明了标准化后的极值存在极限分布。针对 $M_n$ 的分布形式我们有如下定理：
Fisher-Tippett 极值类型定理： 设$X_1,X_2,\dots ,X_n$ 为独立同分布的随机变量序列，如果存在常数列 $a_n>0$ 和 $\{b_n\}$ 使得$$\underset{n\to \infty }{\lim }Pr(\frac{M_n-b_n}{a_n}\le x)=H(x),x\in R$$成立，其中 $H(x)$ 是非退化的分布函数，那么 $H(x)$ 必定属于下列三种类型之一：
$$F(x;\mu ,\sigma )=P\{M_n\le x\}=\{\begin{array}{l}{e}^{-e^{-\frac{x-\mu }{\sigma }}},-\infty <x<\infty ,(第一型)\\ \{\begin{array}{l}0,x\le \mu \\ e^{-(\frac{x-\mu }{\sigma }{)}^{-\alpha }},x>\mu \end{array},\alpha >0,(第二型)\\ \{\begin{array}{l}{e}^{-(-\frac{x-\mu }{\sigma }{)}^{\alpha }},x\le \mu ,\\ 1,x>\mu ,\end{array},\alpha >0,(第三型)\end{array}$$其中一型、第二型和第三型极值分布分别称为 Gumbel分布、Frechet分布、Weibull分布。当 $\alpha =1$ 时，上述极值分布称为标准的极值分布，称 $a_n$ 与 $b_n$ 为规范化参数。
极值类型定理说明，如果 $M_n$ 经线性变换后，对应的规范化变量 $M_n^{\ast }=(M_n-b_n)/a_n$ 依分布收敛于某一非退化分布，那么，不论底分布 $F(x)$ 是何种分布，这个极限分布必定属于极值分布的三种类型之一。

Jekinson将这三种极值分布合为一个，提出了广义极值分布。若随机变量 $X$ 服从广义极值分布，则其概率密度函数为
$$f(x)=\frac{1}{\sigma }[1+\xi (\frac{x-\mu }{\sigma }){]}^{-\frac{1}{\xi }-1}exp[1+\xi (\frac{x-\mu }{\sigma }){]}^{-\frac{1}{\xi }}，$$其分布函数为 $$F(x;\mu ,\sigma ,\xi )=exp\{-(1+\xi \frac{x-\mu }{\sigma }{)}^{-\frac{1}{\xi }}\}，$$其中

• $1+\xi (\frac{x-\mu }{\sigma })>0$
• $\xi$ 表示形状参数决定了分布的尾部形状
• $-\infty <\mu <\infty$ 为位置参数
• $\sigma >0$是尺度参数。

特别当 $\mu =0,\sigma =1$ 时，称为标准广义极值分布。
当 $\xi >0$ 时，分布的尾部较长，趋向于Frechet分布；
当 $\xi =0$ 时，分布的尾部呈指数状，趋向于Gumbel分布；
当 $\xi <0$ 时，分布具有有限的上端点，趋向于Weibull分布；

matlab相关操作同I类型极值分布前面加g

1. gevrnd() 生成广义极值分布随机数，生成服从极大值极值分布
   语法

R = evrnd(k, mu, sigma)%产生形状参数为k，位置参数为mu，尺度参数为sigma的随机数
R = evrnd(k, mu, sigma, m, n,...)
R = evrnd(k, mu, sigma, [m, n, ...])

附录----数据介绍

完全数据(complete data)： 在研究过程中，如果能够明确的观察记录到每个研究对象的生存时间，或发生终点事件的具体时间，称这类数据为完全数据。其中生存时间是指从规定的观察起点到发生某一特定终点事件之间经历的时间跨度。
删失数据（Censoring data）: 如果在研究结束的时候，研究对象发生了研究之外的其他事件或生存结局，无法明确的观察记录到发生终点事件的生存时间，称这类数据为删失数据，或不完整数据
右删失（right censored） 指在进行随访观察中，研究对象观察的起始时间已知，但终点事件发生的时间未知，无法获取具体的生存时间，只知道生存时间大于观察时间，这种类型的生存时间称为右删失。右删失是实际研究中最常见的数据删失类型，根据观察结束时间的不同，可以分为：

• I型删失
  所有研究对象的观察起点时间是统一的，在研究随访的过程中，除了已经发生终点事件的研究对象外，其余研究对象的观察时间统一截止到某一固定的时间，这种删失类型即为I型删失。I型删失的删失时间是固定的，因此又称为定时删失。I型删失不允许个体在研究的过程中退出。
• II型删失
  所有研究对象的观察起点时间是统一的，在研究的过程中，一直随访观察到有足够数量的终点结局事件发生为止，此时研究停止，未发生终点事件的研究对象的生存时间未知，这种删失类型即为II型删失。II型删失可以理解为删失比例是事先已经设定的。
• III型删失
  在实际的研究过程中，往往不能保证所有研究对象在同一时间同时进入研究，在研究开始后，随着研究对象的陆续招募进入研究，不同研究对象的观察起始时间有先有后。同时，在研究结束前，有些研究对象已经发生终点事件，可以记录其准确的生存时间，但也有些研究对象中途退出研究，或者在研究结束时仍然未发生终点事件，他们的生存时间无法明确。
  左删失（right censored）： 假设研究对象在某一时刻开始进入研究接受观察，但是在该时间点之前，研究所感兴趣的时间点已经发生，但无法明确具体时间，这种类型即为左删失数据。
  区间删失（right censored）： 在实际的研究中，如果不能够进行连续的观察随访，只能预先设定观察时间点，研究人员仅能知道每个研究对象在两次随访区间内是否发生终点事件，而不知道准确的发生时间，这种删失类型称为区间删失。

参考文献

【1】樊利利，王艳永，2017. 广义极值分布的参数估计及实例分布，38(3), 13-17.
【2】Gnedenko B. Sur la distribution limite du terme d’ une serie aleatoire[J], Ann Math, 1943, 44: 423-453.
【3】Jenkinson A F. The frequency distribution of the annual maximum(or minimum) of meteorological elements[J]. The Quarterly Journal of the Royal Meteorological Society, 1955, 81: 158-197.