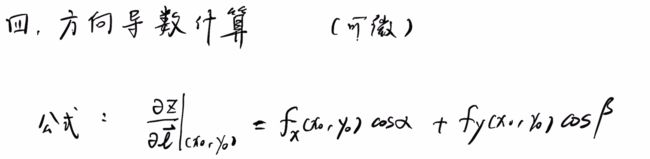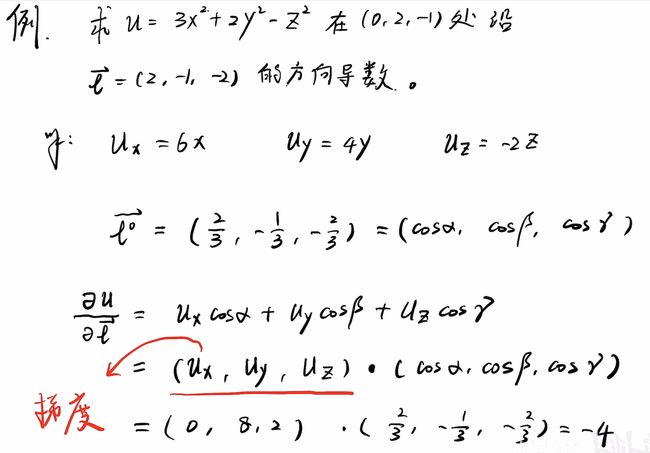高数--猴博士爱讲课
重点章节:
导数/微分/积分
梯度
泰勒展开公式
第一课 求极限
求极限-函数
例一:试求 l i m x − > 3 ( x 2 + 3 ) = 3 2 + 2 = 12 例二:试求 l i m x − > 0 s i n x = s i n 0 = 0 例一:试求 \mathop{lim}_{x->3}{(x^2+3)}=3^2+2=12\\ 例二:试求 \mathop{lim}_{x->0}{sinx}=sin0=0 例一:试求limx−>3(x2+3)=32+2=12例二:试求limx−>0sinx=sin0=0
常见的求导
∞/∞型
0/0型
1∞型
记住这个公式即可。
xy=(elnx)y
0·∞型
将其转换为0/0或者∞/∞型
左右极限
试证明 l i m x − > 0 1 x 是否存在 试证明 \mathop{lim}_{x->0}{\frac{1}{x}}是否存在 试证明limx−>0x1是否存在
做题步骤:
①求函数的左极限②求函数的右极限
③若左极限=右极限=不为oo的数,则函数极限存在,且函数极限=左极限=右极限;若为其他情况,则函数极限不存在/函数没有极限
l i m x − > 0 − 1 x = − ∞ , l i m x − > 0 + 1 x = + ∞ 所以极限不存在 \mathop{lim}_{x->0^-}{\frac{1}{x}}=-∞,\\ \mathop{lim}_{x->0^+}{\frac{1}{x}}=+∞\\ 所以极限不存在 limx−>0−x1=−∞,limx−>0+x1=+∞所以极限不存在
已知f’(X0)=?,求某极限
根据导数的定义,记住两个公式:
求极限-数列
1/3 分析an的取值范围
2/3 证明an的极限存在
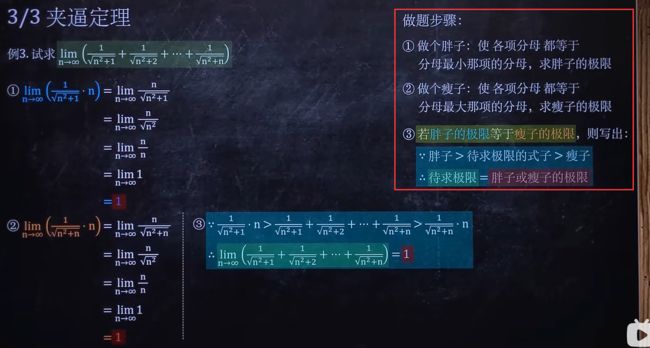
3/3 夹逼定理
第二课《连续、间断点》
函数连续不连续是要看区间的
1/3 证明f(x)在某点连续
例一:试证明 f ( x ) = { s i n x x , x > 0 1 , x ≤ 0 在 x = 0 处连续 例一:试证明f(x)= \begin{cases} \frac{sinx}{x},x>0 \\ 1,x≤0 \end{cases} 在x=0处连续 例一:试证明f(x)={xsinx,x>01,x≤0在x=0处连续
做题步骤:
① f ( 0 ) = 1 l i m x − > 0 − f ( x ) = l i m x − > 0 − 1 = 1 , l i m x − > 0 + f ( x ) = l i m x − > 0 + s i n x x = l i m x − > 0 + x x = l i m x − > 0 + 1 = 1 ② ∵ f ( 0 ) = l i m x − > 0 − f ( x ) = l i m x − > 0 + f ( x ) 成立 ∴ f ( x ) 在 x = 0 处连续 ①f(0)=1 \\ \mathop{lim}_{x->0^-}{f(x)}=\mathop{lim}_{x->0^-}1=1,\\ \mathop{lim}_{x->0^+}{f(x)}=\mathop{lim}_{x->0^+}{\frac{sinx}{x}}=\mathop{lim}_{x->0^+}{{\frac{x}{x}}}=\mathop{lim}_{x->0^+}1=1\\ ②∵f(0)=\mathop{lim}_{x->0^-}{f(x)}=\mathop{lim}_{x->0^+}{f(x)}成立\\ ∴f(x)在x=0处连续 ①f(0)=1limx−>0−f(x)=limx−>0−1=1,limx−>0+f(x)=limx−>0+xsinx=limx−>0+xx=limx−>0+1=1②∵f(0)=limx−>0−f(x)=limx−>0+f(x)成立∴f(x)在x=0处连续
2/3 已知f(x)在某点连续,求未知数
例二:若函数 f ( x ) = { s i n x a x , x > 0 1 , x ≤ 0 在 x = 0 处连续 , 试求 a 例二:若函数f(x)= \begin{cases} \frac{sinx}{ax},x>0 \\ 1,x≤0 \end{cases} 在x=0处连续,试求a 例二:若函数f(x)={axsinx,x>01,x≤0在x=0处连续,试求a
做题步骤
① f ( 0 ) = 1 l i m x − > 0 − f ( x ) = l i m x − > 0 − 1 = 1 , l i m x − > 0 + f ( x ) = l i m x − > 0 + s i n x a x = l i m x − > 0 + x a x = l i m x − > 0 + 1 a = 1 a ② ∵ f ( x ) 在 x = 0 处连续 , 所以 f ( 0 ) = l i m x − > 0 − f ( x ) = l i m x − > 0 + f ( x ) 成立 ∴ a = 1 ①f(0)=1 \\ \mathop{lim}_{x->0^-}{f(x)}=\mathop{lim}_{x->0^-}1=1,\\ \mathop{lim}_{x->0^+}{f(x)}=\mathop{lim}_{x->0^+}{\frac{sinx}{ax}}=\mathop{lim}_{x->0^+}{{\frac{x}{ax}}}=\mathop{lim}_{x->0^+}\frac{1}{a}=\frac{1}{a}\\ ②∵f(x)在x=0处连续,所以f(0)=\mathop{lim}_{x->0^-}{f(x)}=\mathop{lim}_{x->0^+}{f(x)}成立\\ ∴a=1 ①f(0)=1limx−>0−f(x)=limx−>0−1=1,limx−>0+f(x)=limx−>0+axsinx=limx−>0+axx=limx−>0+a1=a1②∵f(x)在x=0处连续,所以f(0)=limx−>0−f(x)=limx−>0+f(x)成立∴a=1
3/3 间断点
例三:试判断 f ( x ) = { − 1 , x < 1 x , x ≥ 1 的间断点类型 例三:试判断f(x)= \begin{cases} -1,x<1 \\ x,x≥1 \end{cases} 的间断点类型 例三:试判断f(x)={−1,x<1x,x≥1的间断点类型
第一类:左右极限存在,这个点可以定义一个x让fx连续就是可去间断点,如果不可以那就是跳跃间断点。
第二类:像是1/x这个函数,x=0就是无穷间断点;fx不为0但是sin或cos后的数为0就是震荡间断点
看看有没有不为∞的值,能使sin、cos后面的式子为∞,且系数不为0。若有,这个点可直接命名为震荡间断点或第二类间断点(震荡)
间断点的概念
若 y = f ( x ) 在 x = x 0 处出现如下三种情况之一,则称 x 0 为 y = f ( x ) 的间断点 : ( 1 ) y = f ( x ) 在点 x 0 处无定义 ( 2 ) y = f ( x ) 在点 x 0 处有定义,但 l i m x − > x 0 f ( x ) 不存在 ( 3 ) y = f ( x ) 在点 x 0 处有定义,但 l i m x − > x 0 f ( x ) 存在,但 l i m x − > x 0 f ( x ) ≠ f ( x 0 ) 据此,我们可以对间断点进行分类 若y=f(x)在x=x_0处出现如下三种情况之一,则称x_0为y=f(x)的间断点:\\ (1)y=f(x)在点x_0处无定义\\ (2)y=f(x)在点x_0处有定义,但\mathop{lim}_{x->x_0}{f(x)}不存在\\ (3)y=f(x)在点x_0处有定义,但\mathop{lim}_{x->x_0}{f(x)}存在,但\mathop{lim}_{x->x_0}{f(x)}≠f(x_0)\\ 据此,我们可以对间断点进行分类 若y=f(x)在x=x0处出现如下三种情况之一,则称x0为y=f(x)的间断点:(1)y=f(x)在点x0处无定义(2)y=f(x)在点x0处有定义,但limx−>x0f(x)不存在(3)y=f(x)在点x0处有定义,但limx−>x0f(x)存在,但limx−>x0f(x)=f(x0)据此,我们可以对间断点进行分类
据此,我们可以对间断点进行分类
做题步骤
第三课《求导》
1/5 照公式求导
常见的求导
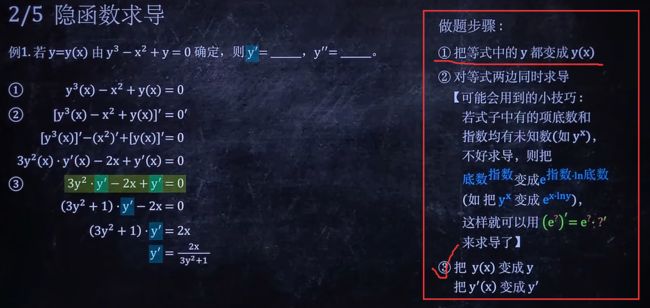
2/5 隐函数求导
例 1. 若 y = y ( x ) 由 y 3 − x 2 + y = 0 确定,则 y ′ = , y ′ ′ = 。 例1.若y=y(x)由y^3-x^2+y=0确定,则y'=_,y''=_。 例1.若y=y(x)由y3−x2+y=0确定,则y′=,y′′=。
求y’'同理上面的步骤对y’求导
3/5 参数方程求导
例三:设 { x = 1 + t 2 y = c o s t , 则 y ′ = , y ′ ′ = 。 例三:设 \begin{cases} x=1+t^2 \\ y=cost \end{cases} ,则y'=_,y''=_。 例三:设{x=1+t2y=cost,则y′=,y′′=。
参数方程求导公式
4/5 求极值、最值
例 3. 若 y = y ( x ) 由 y 3 一 x 2 + y = 0 确定 , 试求其极值 , 以及 x ∈ [ 0 , 1 ] 时的最值 例3.若y=y(x)由y^3一x^2+y=0确定,试求其极值,以及x∈[0,1]时的最值 例3.若y=y(x)由y3一x2+y=0确定,试求其极值,以及x∈[0,1]时的最值
做题步骤
【知识点回忆】
y’'>0说明在这个点的一阶导数有从0开始增大的趋势,也就是说函数有增加的趋势【函数图像凹】
5/5 求凹凸区间与拐点
例 4. 求曲线 y = l n ( x 2 + 1 ) 的凹凸区间和拐点 例4.求曲线y=ln(x^2+1)的凹凸区间和拐点 例4.求曲线y=ln(x2+1)的凹凸区间和拐点
方法:求y"
凸区间:满足y"<0的区间凹区间:满足y">0的区间
拐点:凹凸区间交界的点
第四课《微分中值定理和导数的应用》
1/3 用罗尔中值定理证明等式
2/3 用拉格朗日中值定理证明关于f(x2)-f(x1)/[x2-x1]的不等式
3/3 求极值与最值
求函数 f ( x ) = 4 x 3 − 12 x 2 + 9 x 的极大值、极小值及在 [ 0 , 1.5 ] 内的最大值 求函数f(x)=4x^3-12x^2+9x的极大值、极小值及在[0,1.5]内的最大值 求函数f(x)=4x3−12x2+9x的极大值、极小值及在[0,1.5]内的最大值

有一块边长为 3 的正方形铁片,在每一个角上各剪去一个边长为 x 的小正方形, 用剩下的部分做成开口盒子,当剪去小正方形的边长 x 为多大时,盒子的容积最大 ? 有一块边长为3的正方形铁片,在每一个角上各剪去一个边长为x的小正方形,\\ 用剩下的部分做成开口盒子,当剪去小正方形的边长x为多大时,盒子的容积最大? 有一块边长为3的正方形铁片,在每一个角上各剪去一个边长为x的小正方形,用剩下的部分做成开口盒子,当剪去小正方形的边长x为多大时,盒子的容积最大?

第五课上《积分-不定积分》
1/6 直接套公式算不定积分
⑧ ∫ t a n x d x = ∫ s i n x c o s x d x = ∫ 1 c o s x d ( − c o s x ) = − l n ∣ c o s x ∣ + C ⑨ ∫ c o t x d x = ∫ 1 t a n x d x = ∫ c o s x s i n x d x = ∫ 1 s i n x d ( s i n x ) = l n ∣ s i n x ∣ + C ( t a n x ) ‘ = s e c 2 x , t a n 2 x + 1 = s e c 2 x [ 十七 ] ∫ d x a 2 + x 2 = ∫ d x a 2 ( 1 + ( x / a ) ) 2 = ∫ d ( x / a ) a ( 1 + ( x / a ) ) 2 = 1 a a r c t a n ( x a ) + C [ 十六 ] ∫ d x a 2 − x 2 = ∫ d x a 1 − ( x / a ) 2 = ∫ d ( x / a ) 1 − ( x / a ) 2 = a r c s i n ( x / a ) + C [ 二十 ] 令 x = a t a n x 和 x = a s e c x 【具体参考张宇基础 30 讲 P 110 】 ⑧ \int tanx dx=\int \frac{sinx}{cosx} dx =\int \frac{1}{cosx} d(-cosx)=-ln|cosx|+C \\ ⑨ \int cotx dx=\int \frac{1}{tanx} dx =\int \frac{cosx}{sinx} dx=\int \frac{1}{sinx} d(sinx)=ln|sinx|+C \\ (tanx)^`=sec^2x,tan^2x+1=sec^2x \\ [十七] \int \frac{dx}{a^2+x^2}=\int \frac{dx}{a^2(1+(x/a))^2}=\int \frac{d(x/a)}{a(1+(x/a))^2}=\frac{1}{a}arctan(\frac{x}{a})+C \\ [十六] \int \frac{dx}{\sqrt{a^2-x^2}}=\int \frac{dx}{a\sqrt{1-(x/a)^2}}=\int \frac{d(x/a)}{\sqrt{1-(x/a)^2}}=arcsin(x/a)+C \\ [二十] 令x=atanx和x=asecx\\ 【具体参考张宇基础30讲P110】 ⑧∫tanxdx=∫cosxsinxdx=∫cosx1d(−cosx)=−ln∣cosx∣+C⑨∫cotxdx=∫tanx1dx=∫sinxcosxdx=∫sinx1d(sinx)=ln∣sinx∣+C(tanx)‘=sec2x,tan2x+1=sec2x[十七]∫a2+x2dx=∫a2(1+(x/a))2dx=∫a(1+(x/a))2d(x/a)=a1arctan(ax)+C[十六]∫a2−x2dx=∫a1−(x/a)2dx=∫1−(x/a)2d(x/a)=arcsin(x/a)+C[二十]令x=atanx和x=asecx【具体参考张宇基础30讲P110】
2/6 设一部分再算的不定积分
换元法
【补充:凑微分法】
3/6 多项相加的不定积分
4/6 两项相乘的不定积分
5/6 sin、cos相乘的不定积分
c o s 2 x = c o s 2 x − s i n 2 x = 2 c o s 2 x − 1 = 1 − 2 s i n 2 x cos2x=cos^2x-sin^2x=2cos^2x-1=1-2sin^2x cos2x=cos2x−sin2x=2cos2x−1=1−2sin2x
6/6 x2加减常数项的不定积分
第五课下《积分-定积分》
1/3 定积分计算
牛顿-莱布尼茨公式
2/3 用定积分求面积
3/3 用定积分求体积
第六课上《微分方程(上)》
1/5 符合y’ + P(x)y =Q(x)的格式,求通解
已知微分方程 y ′ + x y = 3 x ,求通解。 已知微分方程 y ′ + y = 3 x ,求通解。 已知微分方程y'+xy=3x,求通解。\\ 已知微分方程y'+y =3x,求通解。 已知微分方程y′+xy=3x,求通解。已知微分方程y′+y=3x,求通解。
2/5 可将x、y拆到等号两边的题目,求通解
变量可分离型
3/5 有复合部分的题目,求通解
可化为变量可分离型
4/5 含y 、y’、y"、不含x的题目,求通解
二阶可降阶微分方程的求解==【缺X型】==
二阶常系数齐次线性微分方程的通解
5/5 含y 、y’、y"、也含x的题目,求通解
二阶常系数齐次线性微分方程的通解==【二阶齐次通解】==
二阶常系数非齐次线性微分方程的特解==【二阶非齐次特解】==
利用性质
重点补充
泰勒展开公式
一、定义:
相比e* ,sin x,cos x, ln(1+x)这些函数,人们对幂函数更为熟悉,如果能把函数近似表达成多项式,并且函数和多项式之间的误差也可以表示,那么在求极限,不等式或其他题目中可能会使形式变得简单,容易计算。
泰勒公式一句话描述:就是**用多项式函数去逼近光滑函数**。
泰勒公式,也称泰勒展开式。是用一个函数在某点的信息,描述其附近取值的公式。如果函数足够平滑,在已知函数在某一点的各阶导数值的情况下,泰勒公式可以利用这些导数值来做系数,构建一个多项式近似函数,求得在这一点的邻域中的值

来自于张宇基础 30 讲 P 87 来自于张宇基础30讲P87 来自于张宇基础30讲P87
二、重要函数的泰勒公式
三、用处
①利用泰勒公式求极限
②常用的等价无穷小
梯度
参考资源:https://www.bilibili.com/video/BV1uZ4y1L7bB/?spm_id_from=333.337.search-card.all.click&vd_source=de55588165743d85bbfd39eae0d9c152
1、方向导数
偏导数
①定义
②计算
③例题
2、梯度
在一个数量场中,函数在给定点处沿不同的方向,其方向导数一般是不相同的,现在我们所关心的是沿哪一个方向其方向导数最大?最大值是多少?函数在点P沿哪一方向增加的速度最快?为此引进一个很重要的概念一一梯度