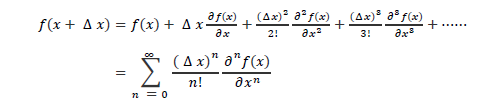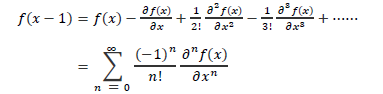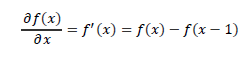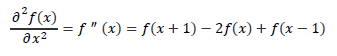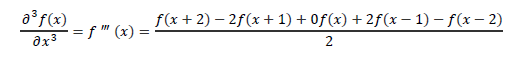Sobel边缘检测算子的本质

  

准备知识：

      我们知道对于一维连续函数f(x)而言，在点x的切线斜率可以用改点的一阶导数表示。但是对于一维的离散函数f(u)而言，我们可以通点u相邻的两函数值定义的直线估算其一阶导数。如下图所示：

即

从泰勒级数的角度求解一阶导数：

一维函数f(x)在任意一点x的一阶导数，可以由f(x+∆x)泰勒级数计算得出：

其中，∆x在数字图像处理中的单位为一个像素。假若∆x=1，则表示采样点x之前的采样点x+1；∆x=-1，则表示采样点之后的采样点x-1。

因此，当∆x=1时，则有：

当∆x=-1时，则有：

在计算图像像素灰度差分的时候，我们可以值利用部分泰勒级数项。针对一阶导数我们可以只利用泰勒级数中的线性项，因此，我们可以通过三种方式表示一阶导数的计算：

由以上两式子，通过前向差分计算其一阶导数：

由以上两式子， 通过后项差分计算其一阶导数：

由以上两式子，通过中心差分计算其一阶导数： 

泰勒级数中未使用的高阶项代表的是实际的一阶导数和估算的一阶导数的误差。一般而言，导数求解中使用越多泰勒级数项，代表求解的值误差越小。实际表明，对于相同数目的点计算其一级导数时，中心差分的误差要小于前向和后向差分。因此，一阶导数的差分常常利用中心差分表示。具体原因可以参考：前向差分、后向差分和中心差分误差分析，同样的道理，我们可以得出二阶导，三阶导.......N阶导。

 

以上是一元函数的一阶导数各种求解法，扩展到二维函数可以用相应的偏导数求解。

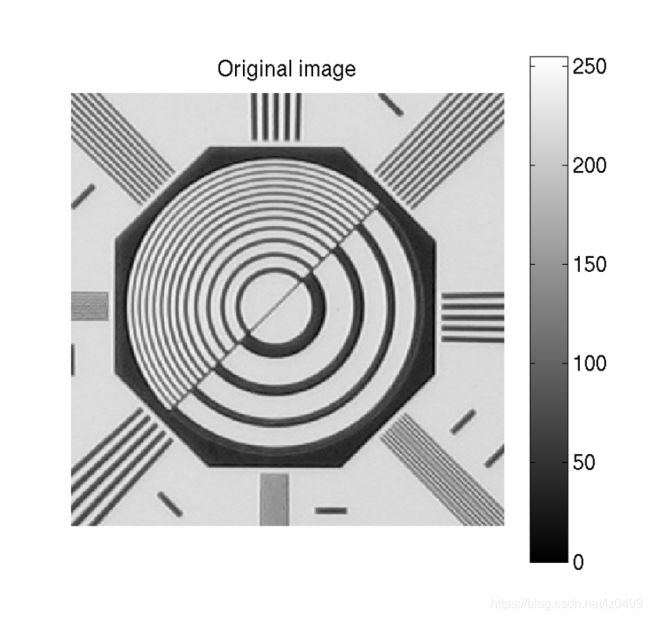
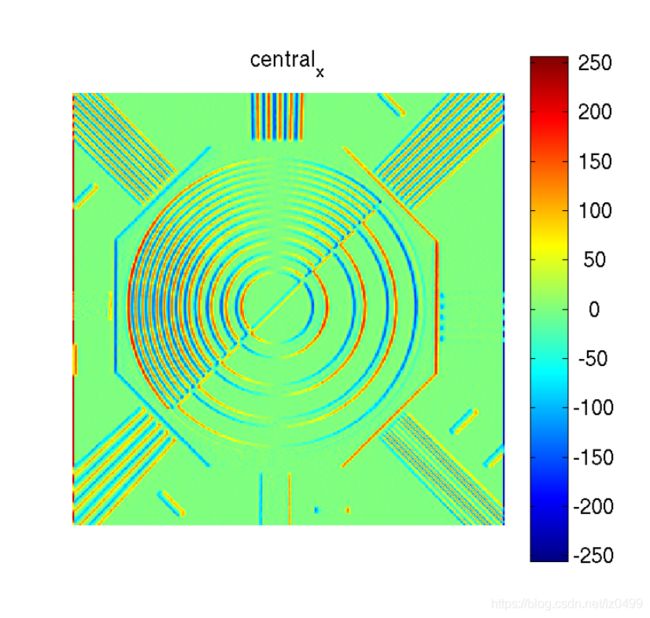
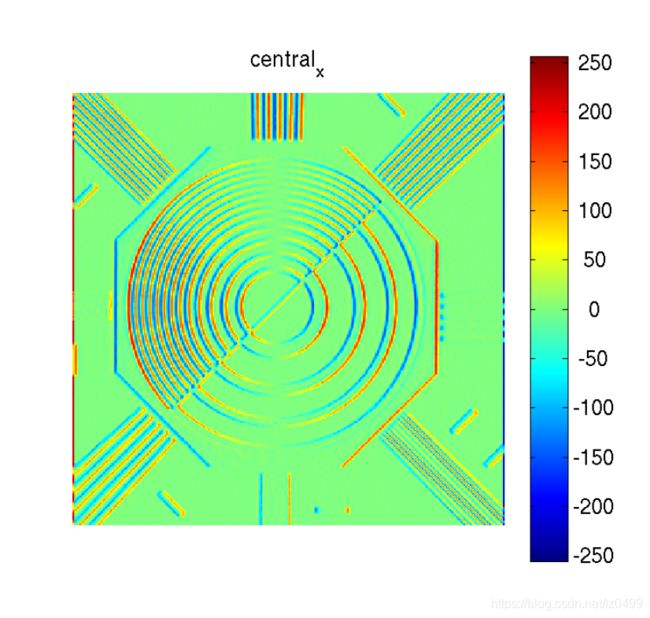
图像中各种一阶导数结果实例：

 

 

 

一、Soel边缘检测算子

    边缘检测类似微分运算，本质是检测图像的亮度变化。例如对于下图中全黑背景中心较亮的图像而言，我们沿着水平某直线定义图像的灰度值函数f(x)，则f(x)的导数可以表示为：

F(x)及其导数可以在坐标上表示为：

      我们可以看到，在灰度值增加的区域其导数为正，在灰度值减小的区域，其导数为负。在灰度值不变的区域其导数为0。

      这是相对平滑的图像而言比较好的结果。对于含噪声的图像，噪声必然会对图像检测结果带来影响。为了避免噪声对检测算子的影响，在构造边缘检测算子的时候不仅需要考虑差分处理，害的考虑平滑处理，这样既能滤除噪声又能检测边缘。类似一阶差分模板，Roberts交叉算子只是考虑了差分因素，而Prewitt他算子通过对一阶差分模板扩展成3*3的尺寸从而引入了均值运算。Sobel算子被认为是较好的检测模板，它考虑差分因素还兼顾了类似高斯平滑的平滑处理。

      可以看到Sobel算子对图像的处理过程，本质是一次差分、一次平滑的连续运算。其中[1 0 -1]及其转置，分别表示水平差分和垂直差分；[1 2 1]及其转置，分别代表水平平滑和垂直平滑。 

     Gx模板由于使用的是水平方向的差分和平滑模板进行卷积，而竖直边缘的水平差分比较大，竖直边缘将会被提取出来；同理，Gy模板使用的是竖直方向的差分和平滑模板进行卷积，而水平边缘的竖直方向的差分会比较大，将会把水平边缘提起出来；

   二、Soel边缘检测分析

      考虑一维信号情况，假设使用一个简单的平均过程来作为低通滤波。通过将三个连续位置的信号的值取平均来替代平滑信号，则有：

                                                  

然后，通过在位置i左右两个相邻信号差值的平均值来估算在i处的导数：

将上述两式子可知： 

      如果模板足够大，可以将平滑和差分这两个线性操作结合进一个操作中。在这种情况下，每个信号的一阶差分可以通过模板，很显然，使用的模板越大，平滑的效果越强，其边缘定为的位置将更加不准确。

     对于二维图像信号而言，可以用来结合平滑和差分的最小模板大小为3*3模板。在这种情况下，我们可以选择一个方向上进行平滑，另一个方向进行差分。即二维信号的模板可以串联先使用3*1的平滑模板，在使用一个1*3的差分模板，或者也可以反过来使用。但在一般情况下，一 个3*3的二维模板具有如下形式：

1	K	1
0	0	0
-1	-K	-1

      上图中，左列表示一个有噪声的信号和它的两个平滑版本，一个使用连续三个样本替代中间值，另一个使用连续九个样本替代。右上图是对原始信号的一阶差分估算，杰每一个样本减去前一个样本的结果。边缘在未平滑的信号中显示为一个尖锐的峰，但是这个输出同时还有若干个较低的峰。当信号从平滑版本计算其一阶差分时，较小的峰数量减少了，同时对于的真实边缘主峰也变钝了。平滑的越厉害，主峰越钝。在对应平滑信号图中，为了方便比较，原始输入和他的差分信号用虚线表示。

二、Soel边缘检测另外一种估算方法

有上述理论可知，Sobel算子可以看作平滑算子和差分算子的卷积，两个算子的共同作用下才能在有噪声的图像中能够检测出边缘。

一般平滑算子使用高斯平滑。我们知道高斯函数的最佳逼近由二项式展开的系数决定，换句话说，用杨辉三角形（也称Pascal三角形）的第n行作为高斯滤波器的一个具有n个点的一维逼近。杨辉三角如下图所示：

因此对于五点的高斯平滑五点逼近为:

1 4 6 4 1

它们对应于Pascal三角形的第5行．这一模板被用来在水平方向上平滑图像。Pascal三角形各行的系数计算公式如下：

因此，在Sobel算子的平滑算子系数也可以根据Pascal三角形得出，其关系如下图所示：

其具体数学计算公式为：

其中，winsize为模板大小，x_win为所在行的位置。假设3*3模板大小的Sobel算子，其平滑算子计算应该为：

Psacal(0,2)=1;   Psacal(1,2)=2;   Psacal(2,2)=1;

因此，3*3模板大小的Sobel算子平滑算子为[1 2 1]

相对应的差分算子，也可以从Pascal三角形中得出。差分算子系数的Pascal三角形为：

 其具体数学计算公式为：

其中，winsize为模板大小，x_win为所在行的位置，范围为[0,winsize-1]。假设3*3模板大小的Sobel算子，其差分算子计算应该为：

Psacal(0,1)-Psacal(-1,1)=1-0=1;

Psacal(1,1)-Psacal(0,1)=1-1=0;

Psacal(2,1)-Psacal(1,1)=0-1=-1;

因此，3*3模板大小的Sobel算子差分算子为[1 0 -1]

故，Gx方向检测竖直边缘的3*3模板大小的Sobel模板为:

Gy方向检测水平边缘的3*3模板大小的Sobel模板为:

参考文献：<>

《Feature extraction & image processing for computer vision(3rd edition)》