MATLAB中的一维插值与函数拟合
本文主要记录Matlab中常用的一维插值与函数拟合的使用方法
文章目录
- 前言
- 一、一维插值
- 二、函数拟合
-
- 2.1 多项式拟合
-
- 2.1.1多项式拟合指令
- 2.1.2 图形窗口的多项式拟合
- 2.2 指定函数拟合
- 参考资料
前言
最近在学习数学建模,这部分关于怎么使用Matlab,刚好记录下来,做电赛的时候这些常用的插值、拟合工具也是需要学习的,刚开始学,写的不好,欢迎大家批评指正。
以下是本篇文章正文内容
一、一维插值
用MATLAB软件求解插值问题
在MATLAB中提供了一个一维插值函数interp1, 它的调用格式为
cy=interp1(x , y , cx , ‘method’)
其中x、y是所给数据的横纵坐标,要求x的分量按升序或降序排列,cx是待求的插值点的横坐标,返回值cy是待求的插值点的纵坐标,method是插值方法, 该函数提供了四种可选的插值方法:
- nearest——最邻近点插值。 点和这两已知点间位置的远近来进行插值,取较近已知 它根据已知两点间的插值 插值点处的函数值作为未知插值点处的函数值。
- linear——线性插值。它将相邻的数据点用直线相连, 按所生成的直线进行插值。
- spline——三次样条插值。它利用已知数据求出样条 函数后,按样条函数进行插值。
- cubic——三次插值。它利用已知数据求出三次多项式 函数后,按三次多项式函数进行插值。(在我的Matlab2019b中名为pchip)
缺省时插值方法为分段线性插值。
下面用该函数来求解下列插值问题。
对于下面给定的4组数据,求在x=110处 y的值。
| x | y |
|---|---|
| 100 | 10 |
| 121 | 11 |
| 144 | 12 |
| 169 | 13 |
很明显,我们可以看出这组数据符合函数y=sqrt(x);
我们用科学计算器得到一个解cy*=10.4880。
接下来我们使用Matlab进行插值计算:
输入命令:
x=[100 121 144 169];
y=[10 11 12 13];
cx=110;
cy1=interp1(x,y,cx,'nearest');
cy2=interp1(x,y,cx,'linear');
cy3=interp1(x,y,cx,'pchip');
cy4=interp1(x,y,cx,'spline');
运行结果依次为 cy1 = 10、cy2 =10.4762、cy3 = 10.4869、cy4 = 10.4877 通过比较cy* = 10.4880,显然三次样条插值的结果最好。
二、函数拟合
2.1 多项式拟合
将数据点按多项式的形式进行拟合,使用最小二乘法可以确定多项式的系数,多项式拟合有指令语句和图形窗口两种方法。
2.1.1多项式拟合指令
polyfit(X,Y,N):多项式拟合,返回降幂排列的多项式系数。
polyval(P,xi):计算多项式的值。
其中,X,Y是数据点的值;N是拟合的最高次幂;P是返回的多项式系数;xi是要求点的横坐标。
例如对下面的数据进行多项式拟合。
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| y | 9 | 7 | 6 | 3 | -1 | 2 | 5 | 7 | 20 |
拟合的命令如下:
x = [1 2 3 4 5 6 7 8 9];
y = [9 7 6 3 -1 2 5 7 20];
P = polyfit(x,y,3);
xi = 0:0.2:10;
yi = polyval(P,xi);
plot(xi,yi,x,y,'r*');
2.1.2 图形窗口的多项式拟合
在图形窗口可以用菜单方式对数据进行简单、快速、搞笑的拟合。与2.1.1数据相同,先画出数据点:
x = [1 2 3 4 5 6 7 8 9];
y = [9 7 6 3 -1 2 5 7 20];
plot(x,y,'r*');
然后在图形窗口单击Tools(工具)->Basic Fitting(基本拟合),打开对话框,并按下图进行操作,其中分别用线性、二阶、三阶对数据进行了多项式拟合,下面的柱状图显示残差,可以看出,进行三阶多项式拟合的效果是最好的,与前述结果一样。

2.2 指定函数拟合
在Matlab中也可以用用户自定义的函数进行拟合。通过下面的例子可以了解用指定函数进行数据拟合的基本方法。
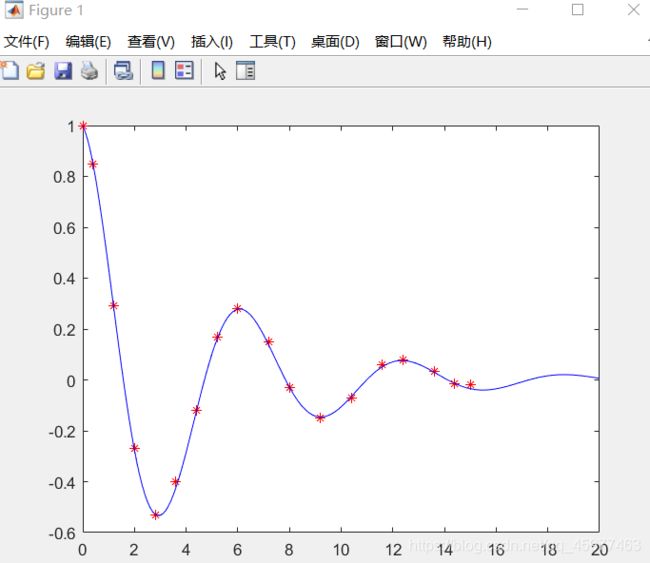
| x | 0 | 0.4 | 1.2 | 2 | 2.8 | 3.6 | 4.4 | 5.2 | 6 | 7.2 | 8 | 9.2 | 10.4 | 11.6 | 12.4 | 13.6 | 14.4 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y | 1 | 0.85 | 0.29 | -0.27 | -0.53 | -0.4 | -0.12 | 0.17 | 0.28 | 0.15 | -0.03 | -0.15 | -0.071 | 0.059 | 0.08 | 0.032 | -0.015 | -0.02 |
在Matlab中先用命令画出上述的散点图:
x = [0 0.4 1.2 2 2.8 3.6 4.4 5.2 6 7.2 8 9.2 10.4 11.6 12.4 13.6 14.4 15];
y = [1 0.85 0.29 -0.27 -0.53 -0.4 -0.12 0.17 0.28 0.15 -0.03 -0.15 -0.071 0.059 0.08 0.032 -0.015 -0.02];
plot(x,y,'r*');

知道其对应的函数形式为 f ( t ) = a c o s ( k t ) e w t f(t) = acos(kt)e^{wt} f(t)=acos(kt)ewt,则可用Matlab进行拟合,程序如下:
syms t
x = [0;0.4;1.2;2;2.8;3.6;4.4;5.2;6;7.2;8;9.2;10.4;11.6;12.4;13.6;14.4;15];
y = [1;0.85;0.29;-0.27;-0.53;-0.4;-0.12;0.17;0.28;0.15;-0.03;-0.15;-0.071;0.059;0.08;0.032;-0.015;-0.02];
f = fittype('a*cos(k*t)*exp(w*t)','independent','t','coefficients',{'a','k','w'});
cfun = fit(x,y,f);
xi = 0:0.1:20;
yi = cfun(xi);
plot(x,y,'r*',xi,yi,'b-');
参考资料
《MATLAB在数学建模中的应用》卓金武《北京航空航天大学出版社》 , 2011.4
有用的话点个赞吧!