实例：【贝叶斯分类器的设计】

---

一、知识要点

最小错误率贝叶斯分类器把样本划分到后验概率最大的那一类中，因此可以定义每一类的判别函数为：
$${\mathbf{g}}_{\mathbf{i}}(x)=p\left(\mathbf{x}\mid {\omega }_{\mathrm{i}}\right)P\left({\omega }_{\mathrm{i}}\right)$$
判别函数中，先验概率是一个与特征向量无关的常量，类条件概率密度则满足一定的概率分布。假设类条件概率符合 d 维正态分布，则判别函数为 ：
$${\mathrm{g}}_{\mathrm{i}}(x)=\frac{P\left({\omega }_{\mathrm{i}}\right)}{(2\pi {)}^{d/2}{\left|{\sum }_i\right|}^{1/2}}\exp \left[-\frac{1}{2}(x-\mu {)}^T\sum _i^{-1}(x-\mu )\right]$$

对数计算后，得到:
$${\mathrm{g}}_{\mathrm{i}}(x)=\ln P\left({\omega }_{\mathrm{i}}\right)-\frac{1}{2}(x-\mu {)}^T\sum _i^{-1}(x-\mu )-\frac{d}{2}\ln 2\pi -\frac{1}{2}\ln \left|{\Sigma }_i\right|$$
假设样本空间被划分为 c 个类别决策区域，则分类判决规则为:
$${\mathrm{g}}_i(x)>{\mathrm{g}}_j(x),i=1,2,\dots ,c,j\ne i\iff x\in {\omega }_i$$
此时任两个类别之间的决策边界由方程${\mathbf{g}}_i(x)-g_j(x)=0$决定。

二、项目内容

有两类样本鲈鱼和鲑鱼，每个样本有两个特征（长度和亮度），每类有50个样本点，假设每类样本点服从二维正态分布，鲈鱼的两个特征的均值向量和协方差矩阵为${\mu }_1=[8,8],\Sigma =\left[\begin{array}{cc}16& 0\\ 0& 16\end{array}\right]$，鲑鱼的两个特征的均值向量和协方差矩阵为${\mu }_2=[15,16],\Sigma =\left[\begin{array}{cc}16& 0\\ 0& 16\end{array}\right]$。
根据贝叶斯公式，给出在类条件概率密度为正态分布时具体的判别函数表达式，用此判别函数设计分类器。可以看出每类的协方差矩阵都相等，类内两个特征维度间相互独立，且方差相同均为16；
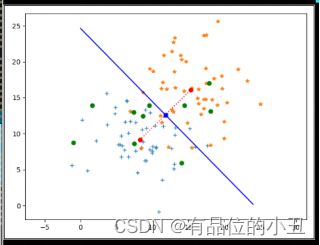
（1）如果两类的先验概率相等，即P（鲈鱼）=P（鲑鱼）=0.5。可以计算每类数据的均值点，并且把两个均值点连成一线段，用垂直平分该线段的直线作为分类边界。再根据该分类边界对一随机给出的样本判别类别。
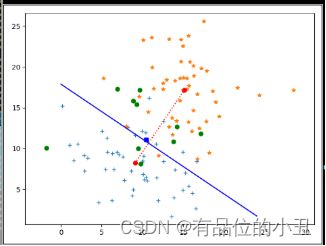
（2）如果两类的先验概率不相等，P（鲈鱼）=0.4，P（鲑鱼）=0.6。此题中判别边界与第一题一样，都是一条直线，且垂直于均值的连线，但不一定通过连线的中点，而是通过x0的表达式为：
$x_0=\frac{1}{2}\left({\mu }_i+{\mu }_j\right)-\frac{{\sigma }^2}{{\Vert {\mu }_i-{\mu }_j\Vert }^2}\ln \frac{P\left({\omega }_i\right)}{P\left({\omega }_j\right)}\left({\mu }_i-{\mu }_j\right)$的点。故在第一题的基础上求出x0，即可求出判别边界的表达式。（分类边界离开先验概率大的一类， 即会有更多的样本被识别为先验概率大的类），再根据该分类边界对一随机给出的样本判别类别。

三、实现

1. 若两类的先验概率相等

此题最主要是把分类边界方程给确定出来。假设分类边界为 kx-y+b=0，即要计算出k和b，其中k为两类样本均值点连线的斜率的负倒数，若两类均值点分别为（x1，y1）、（x2，y2），则$k=-\frac{x_1-x_2}{y_1-y_2}$；由于分类边界为两均值连线的垂直平分线，故两均值点的中点必在分类边界上，假设中点位（xm，ym），则$b=y_m-k{x}_m$，那么分类边界即可求出了。

1.1 设置两类样本数

import numpy as np
from matplotlib import pyplot as plt
import math
#设置样木数量
n=50
#鲈鱼特征
mean1 = np.array([8,8])
cov = [[16, 0], [0, 16]]
#鲈鱼样木
x1 = np.random.multivariate_normal(mean1, cov, n)
#鲑鱼特征
mean2 = np.array([15,16])
#鲑鱼样木
x2 = np.random.multivariate_normal(mean2,cov, n)
#axis = 0：压缩行，对各列求均值，返回 1* n 矩阵
M1=np.mean(x1,axis=0)
C1=np.cov(x1.T)
M2=np.mean(x2,axis=0)
C2=np.cov(x2.T)
#设置xy轴单位长度比例都-样
plt.axis('equal')
#显示两类样本，第一类鲈鱼用+,第二类鲑鱼用*
plt.plot(x1[:,0],x1[:,1],'+')
plt.plot(x2[:,0],x2[:,1],'*')

1.2 计算两类的均值点，画出连线

#计算均值两点，画出了一条连接线，虚线红色
xx=(M1[0],M2[0])
yy=(M1[1],M2[1])
plt.plot(xx,yy, 'ro', ls='dotted')

1.3 画出中垂线

#计算这条连接线的斜率k1
k1 =(M2[1]-M1[1])/(M2[0]-M1[0])
#计算垂线的斜率k2 (已知两条垂线的斜率相乘为1)
k2 = -1/k1
#计算中间点坐标
xx2 = (M1[0]+M2[0])/2
yy2 = (M1[1]+M2[1])/2
#计算垂线b值，b=y-kx
b = yy2 - k2 * xx2
#画出x为(0, 25)之间的这条直线，即垂线，过中点b，斜率为k2
x = np.arange(0,25)
#直线方程为
y =k2 * x + b
#显示中点坐标，蓝色正方形
plt.plot(xx2, yy2,'bs')
#显示垂线，蓝色表示
plt.plot(x,y,'b')

1.4 新建10个样本，判断它们分别属于哪一类？

#新建10个样木，绿色圆圈表示
nx = np.random.multivariate_normal([10,12],cov,10)
plt.plot(nx[: ,0],nx[:,1],'go')
#显示所有图形
plt.show()

结果展示：

2. 若两类的先验概率不等

如果两类的先验概率不相等；此题中判别边界与第一题一样，都是一条直线，且垂直于均值的连线，但不一定通过连线的中点，而是通过x0的表达式为: $x_0=\frac{1}{2}\left({\mu }_i+{\mu }_j\right)-\frac{{\sigma }^2}{{\Vert {\mu }_i-{\mu }_j\Vert }^2}\ln \frac{P\left({\omega }_i\right)}{P\left({\omega }_j\right)}\left({\mu }_i-{\mu }_j\right)$的点。故在第一题的基础上求出x0，即可求出判别边界的表达式。

2.1 设置两类样本数

import numpy as np
from matplotlib import pyplot as plt
import math
#设置样木数量
n=50
#鲈鱼特征
mean1 = np.array([8,8])
cov = [[16, 0], [0, 16]]
#鲈鱼样木
x1 = np.random.multivariate_normal(mean1, cov, n)
#鲑鱼特征
mean2 = np.array([15,16])
#鲑鱼样木
x2 = np.random.multivariate_normal(mean2,cov, n)
M1=np.mean(x1,axis=0)
C1=np.cov(x1.T)
M2=np.mean(x2,axis=0)
C2=np.cov(x2.T)
plt.axis('equal')
#显示两类样本，第一类鲈鱼用+,第二类鲑鱼用*
plt.plot(x1[:,0],x1[:,1],'+')
plt.plot(x2[:,0],x2[:,1],'*')

2.2 计算两类的均值点，画出连线

#计算均值两点，画出了一条连接线，虚线红色
xx=(M1[0],M2[0])
yy=(M1[1],M2[1])
plt.plot(xx,yy, 'ro', ls='dotted')

2.3 根据x0坐标画出分类垂线

*x0=1/2*(mean1+mean2)-(C1[0][0]/(mean1-mean2).T)*math.log(2/3)*
#计算这条连接线的斜率k1
k1 =(M2[1]-M1[1])/(M2[0]-M1[0])
#计算垂线的斜率k2 (已知两条垂线的斜率相乘为1)
k2 = -1/k1
#计算垂点坐标
x0=1/2*(mean1+mean2)-(C1[0][0]/(mean1-mean2).T)*math.log(2/3)
#计算垂线b值，b=y-kx
b = x0[0] - k2 * x0[1]
#画出x为(0, 25)之间的这条直线，即垂线，过b，斜率为k2
x = np.arange(0,25)
#直线方程为
y =k2 * x + b
#显示中点坐标，蓝色正方形
plt.plot(x0[0], x0[1],'bs')
#显示垂线，蓝色表示
plt.plot(x,y,'b')

2.4 新建10个样本，判断它们分别属于哪一类？

#新建10个样木，绿色圆圈表示
nx = np.random.multivariate_normal([10,12],cov,10)
plt.plot(nx[: ,0],nx[:,1],'go')
#显示所有图形
plt.show()

结果展示：