超参数优化(网格搜索和贝叶斯优化)
超参数优化
- 1 超参数优化
-
- 1.1 网格搜索类
-
- 1.1.1 枚举网格搜索
- 1.1.2 随机网格搜索
- 1.1.3 对半网格搜索(Halving Grid Search)
- 1.2 贝叶斯超参数优化(推荐)
-
- 原理
- 1.2.1 BayesOpt实现高斯过程GP(较慢)
-
- 1.2.1.1 定义目标函数
- 1.2.1.2 定义参数空间
- 1.2.1.3 定义优化目标函数和具体流程
- 1.2.1.4 验证(非必要)
- 1.2.1.5 执行
- 1.2.2 hyperopt贝叶斯方法(推荐)
-
- 1.2.2.1 导包--导入数据--init初始学习器的建立
- 1.2.2.2 定义目标函数
- 1.2.2.3 参数空间的确定
- 1.2.2.4 定义优化目标函数
- 1.2.2.5 验证函数(非必要)
- 1.2.2.6 执行和建议
- 1.2.3 基于Optuna实现多种贝叶斯优化(推荐)
-
- 1.2.3.1 定义目标函数与参数空间
- 1.2.3.2 定义优化目标函数的具体流程
- 1.2.3.3 执行实际优化流程
- 结果求出后,可继续减小参数空间范围,增大参数密度,进一步优化目标参数组合
- 模型存储和读取
1 超参数优化
scoring:
import sklearn
sorted(sklearn.metrics.SCORERS.keys())
1.1 网格搜索类
1.1.1 枚举网格搜索
classsklearn.model_selection.GridSearchCV(estimator, param_grid, , scoring=None, n_jobs=None, refit=True, cv=None, verbose=0, pre_dispatch='2n_jobs', error_score=nan, return_train_score=False)
https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html#sklearn.model_selection.GridSearchCV
| Name | Description |
|---|---|
| estimator | 调参对象,某评估器 |
| param_grid | 参数空间,可以是字典或者字典构成的列表,稍后介绍参数空间的创建方法 |
| scoring | 评估指标,支持同时输出多个参数 |
| n_jobs | 设置工作时参与计算的线程数 |
| refit | 挑选评估指标和最佳参数,在完整数据集上进行训练 |
| cv | 交叉验证的折数 |
| verbose | 输出工作日志形式 |
| pre_dispatch | 多任务并行时任务划分数量 |
| error_score | 当网格搜索报错时返回结果,选择’raise’时将直接报错并中断训练过程,其他情况会显示警告信息后继续完成训练 |
| return_train_score | 在交叉验证中是否显示训练集中参数得分 |
- 主要是范围合适,枚举网格搜索能完成最优解的搜索,就是太费时间
import time #计时模块time
import pandas as pd
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.model_selection import KFold, GridSearchCV
def RMSE(cvresult,key):
return (abs(cvresult[key])**0.5).mean()
data = pd.read_csv( r"D:\学习资料\sklearn课件\AutoML与超参数优化——菜菜\train_encode.csv", index_col=0)
X = data.iloc[:,:-1]
y = data.iloc[:,-1]
param_grid_simple = {'n_estimators': [*range(5,100,5)]
, 'max_depth': [*range(25,36,2)]
, "max_features": ["log2","sqrt","auto"]
}
reg = RFR(random_state=1412,verbose=True,n_jobs=-1)
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
search = GridSearchCV(estimator=reg
,param_grid=param_grid_simple
,scoring = "neg_mean_squared_error" #MSE
,verbose = True
,cv = cv
,n_jobs=12)
#=====【TIME WARNING: 5~10min】=====#
start = time.time()
search.fit(X,y)
print(time.time() - start)
search.best_estimator_
"""
RandomForestRegressor(max_depth=33, max_features='log2', n_estimators=45,
n_jobs=-1, random_state=1412, verbose=True)
"""
abs(search.best_score_)**0.5
# 29840.676988215626
1.1.2 随机网格搜索
决定枚举网格搜索运算速度的因子一共有两个:
- 参数空间的大小:参数空间越大,需要建模的次数越多
- 数据量的大小:数据量越大,每次建模时需要的算力和时间越多
所以解决方式就俩:
- 调整搜索空间
- 每次训练的数据。
在sklearn中,随机抽取参数子空间并在子空间中进行搜索的方法叫做随机网格搜索RandomizedSearchCV。
随机网格搜索在实际运行时,并不是先抽样出子空间,再对子空间进行搜索,而是逐个的,这种随机抽样是不放回的。我们可以控制随机网格搜索的迭代次数。
class sklearn.model_selection.RandomizedSearchCV(estimator, param_distributions, *, n_iter=10, scoring=None, n_jobs=None, refit=True, cv=None, verbose=0, pre_dispatch='2*n_jobs', random_state=None, error_score=nan, return_train_score=False)
https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RandomizedSearchCV.html#sklearn.model_selection.RandomizedSearchCV
| Name | Description |
|---|---|
| estimator | 调参对象,某评估器 |
| param_distributions | 全域参数空间,可以是字典或者字典构成的列表 |
| n_iter | 迭代次数,迭代次数越多,抽取的子参数空间越大 |
| scoring | 评估指标,支持同时输出多个参数 |
| n_jobs | 设置工作时参与计算的线程数 |
| refit | 挑选评估指标和最佳参数,在完整数据集上进行训练 |
| cv | 交叉验证的折数 |
| verbose | 输出工作日志形式 |
| pre_dispatch | 多任务并行时任务划分数量 |
| random_state | 随机数种子 |
| error_score | 当网格搜索报错时返回结果,选择’raise’时将直接报错并中断训练过程,其他情况会显示警告信息后继续完成训练 |
| return_train_score | 在交叉验证中是否显示训练集中参数得分 |
import time #计时模块time
import pandas as pd
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.model_selection import KFold, RandomizedSearchCV
#创造参数空间 - 使用与网格搜索时完全一致的空间
param_grid_simple = {'n_estimators': [*range(5,100,5)]
, 'max_depth': [*range(25,36,2)]
, "max_features": ["log2","sqrt","auto"]
}
#建立回归器、交叉验证
reg = RFR(random_state=1412,verbose=True,n_jobs=12)
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
#计算全域参数空间大小,因为要是不知道全域大小,就不知道在随机网格搜索中的迭代量
len([*range(5,100,5)]) * len([*range(25,36,2)]) * 3
# 342
search = RandomizedSearchCV(estimator=reg
,param_distributions=param_grid_simple
,n_iter = 170 #子空间的大小是全域空间的约一半
,scoring = "neg_mean_squared_error"
,verbose = True
,cv = cv
,n_jobs=12)
#训练随机搜索评估器
#=====【TIME WARNING: 2~5min】=====#
start = time.time()
search.fit(X,y)
print(time.time() - start)
#查看模型结果
search.best_estimator_
"""
RandomForestRegressor(max_depth=35, max_features='log2', n_estimators=45,
n_jobs=12, random_state=1412, verbose=True)
"""
abs(search.best_score_)**0.5
# 29840.676988215626
# 居然和枚举网格搜索一模一样。
随机网格搜索能够有效的根本原因在于:
- 抽样出的子空间反馈出与全域空间相似的分布
- 子空间越大,子空间与全域空间越相似
- 在与全域空间相似的空间中,随机搜索即便不能找到真正的最小值,也能找到与最小值高度接近的某一个次小值
相似分布的直观形式:
![]()
![]()
1.1.3 对半网格搜索(Halving Grid Search)
在讲解随机网格搜索之前,我们梳理了决定枚举网格搜索运算速度的因子:
1 参数空间的大小:参数空间越大,需要建模的次数越多
2 数据量的大小:数据量越大,每次建模时需要的算力和时间越多
面对枚举网格搜索过慢的问题,sklearn中呈现了两种优化方式:其一是调整搜索空间,其二是调整每次训练的数据。调整搜索空间的方法就是随机网格搜索,而调整每次训练数据的方法就是对半网格搜索。
假设现在存在数据集 D D D,我们从数据集 D D D中随机抽样出一个子集 d d d。如果一组参数在整个数据集 D D D上表现较差,那大概率这组参数在数据集的子集 d d d上表现也不会太好。反之,如果一组参数在子集 d d d上表现不好,我们也不会信任这组参数在全数据集 D D D上的表现。参数在子集与全数据集上反馈出的表现一致,如果这一假设成立,那在网格搜索中,比起每次都使用全部数据来验证一组参数,或许我们可以考虑只带入训练数据的子集来对超参数进行筛选,这样可以极大程度地加速我们的运算。
但在现实数据中,这一假设要成立是有条件的,即任意子集的分布都与全数据集D的分布类似。当子集的分布越接近全数据集的分布,同一组参数在子集与全数据集上的表现越有可能一致。根据之前在随机网格搜索中得出的结论,我们知道子集越大、其分布越接近全数据集的分布,但是大子集又会导致更长的训练时间,因此为了整体训练效率,我们不可能无限地增大子集。这就出现了一个矛盾:大子集上的结果更可靠,但大子集计算更缓慢。对半网格搜索算法设计了一个精妙的流程,可以很好的权衡子集的大小与计算效率问题,我们来看具体的流程:
1、首先从全数据集中无放回随机抽样出一个很小的子集 d 0 d_0 d0,并在 d 0 d_0 d0上验证全部参数组合的性能。根据 d 0 d_0 d0上的验证结果,淘汰评分排在后1/2的那一半参数组合
2、然后,从全数据集中再无放回抽样出一个比 d 0 d_0 d0大一倍的子集 d 1 d_1 d1,并在 d 1 d_1 d1上验证剩下的那一半参数组合的性能。根据 d 1 d_1 d1上的验证结果,淘汰评分排在后1/2的参数组合
3、再从全数据集中无放回抽样出一个比 d 1 d_1 d1大一倍的子集 d 2 d_2 d2,并在 d 2 d_2 d2上验证剩下1/4的参数组合的性能。根据 d 2 d_2 d2上的验证结果,淘汰评分排在后1/2的参数组合……
持续循环。如果使用S代表首次迭代时子集的样本量,C代表全部参数组合数,则在迭代过程中,用于验证参数的数据子集是越来越大的,而需要被验证的参数组合数量是越来越少的:
| 迭代次数 | 子集样本量 | 参数组合数 |
|---|---|---|
| 1 | S | C |
| 2 | 2S | 1 2 \frac{1}{2} 21C |
| 3 | 4S | 1 4 \frac{1}{4} 41C |
| 4 | 8S | 1 8 \frac{1}{8} 81C |
| …… |
当备选参数组合只剩下一组,或剩余可用的数据不足,循环就会停下,具体地来说,当 1 n \frac{1}{n} n1C <= 1或者nS > 总体样本量,搜索就会停止。在实际应用时,哪一种停止条件会先被触发,需要看实际样本量及参数空间地大小。同时,每次迭代时增加的样本量、以及每次迭代时不断减少的参数组合都是可以自由设定的。
在这种模式下,只有在不同的子集上不断获得优秀结果的参数组合能够被留存到迭代的后期,最终选择出的参数组合一定是在所有子集上都表现优秀的参数组合。这样一个参数组合在全数据上表现优异的可能性是非常大的,同时也可能展现出比网格/随机搜索得出的参数更大的泛化能力。
- 对半网格搜索的局限性
然而这个过程当中会存在一个问题:子集越大时,子集与全数据集D的分布会越相似,但整个对半搜索算法在开头的时候,就用最小的子集筛掉了最多的参数组合。如果最初的子集与全数据集的分布差异巨大的化,在对半搜索开头的前几次迭代中,就可能筛掉许多对全数据集D有效的参数,因此对半网格搜索最初的子集一定不能太小。
在对半网格搜索过程中,子集的样本量时呈指数级增长:
对于对半网格搜索应用来说,最困难的部分就是决定搜索本身复杂的参数组合。在调参时,如果我们希望参数空间中的备选组合都能够被充分验证,则迭代次数不能太少(例如,只迭代3次),因此factor不能太大。但如果factor太小,又会加大迭代次数,同时拉长整个搜索的运行时间。因此,我们一般考虑以下两个点:
1、min_resources的值不能太小,且迭代过程中使用尽量多的数据
2、迭代完毕之后,剩余的验证参数组合不能太多,10~20之间即可接受
对半网格搜索的类如下所示:
class sklearn.model_selection.HalvingGridSearchCV(estimator, param_grid, *, factor=3, resource='n_samples', max_resources='auto', min_resources='exhaust', aggressive_elimination=False, cv=5, scoring=None, refit=True, error_score=nan, return_train_score=True, random_state=None, n_jobs=None, verbose=0)
全部参数如下所示:
| Name | Description |
|---|---|
| estimator | 调参对象,某评估器 |
| param_grid | 参数空间,可以是字典或者字典构成的列表 |
| factor | 每轮迭代中新增的样本量的比例,同时也是每轮迭代后留下的参数组合的比例 |
| resource | 设置每轮迭代中增加的验证资源的类型 |
| max_resources | 在一次迭代中,允许被用来验证任意参数组合的最大样本量 |
| min_resources | 首次迭代时,用于验证参数组合的样本量r0 |
| aggressive_elimination | 是否以全部数被使用完成作为停止搜索的指标,如果不是,则采取措施 |
| cv | 交叉验证的折数 |
| scoring | 评估指标,支持同时输出多个参数 |
| refit | 挑选评估指标和最佳参数,在完整数据集上进行训练 |
| error_score | 当网格搜索报错时返回结果,选择’raise’时将直接报错并中断训练过程 其他情况会显示警告信息后继续完成训练 |
| return_train_score | 在交叉验证中是否显示训练集中参数得分 |
| random_state | 控制随机抽样数据集的随机性 |
| n_jobs | 设置工作时参与计算的线程数 |
| verbose | 输出工作日志形式 |
https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.HalvingGridSearchCV.html#sklearn.model_selection.HalvingGridSearchCV
| Name | Description |
|---|---|
| estimator | 调参对象,某评估器 |
| param_grid | 参数空间,可以是字典或者字典构成的列表 |
| factor | 每轮迭代中新增的样本量的比例,同时也是每轮迭代后留下的参数组合的比例 |
| resource | 设置每轮迭代中增加的验证资源的类型 |
| max_resources | 在一次迭代中,允许被用来验证任意参数组合的最大样本量 |
| min_resources | 首次迭代时,用于验证参数组合的样本量r0 |
| aggressive_elimination | 是否以全部数被使用完成作为停止搜索的指标,如果不是,则采取措施 |
| cv | 交叉验证的折数 |
| scoring | 评估指标,支持同时输出多个参数 |
| refit | 挑选评估指标和最佳参数,在完整数据集上进行训练 |
| error_score | 当网格搜索报错时返回结果,选择’raise’时将直接报错并中断训练过程 其他情况会显示警告信息后继续完成训练 |
| return_train_score | 在交叉验证中是否显示训练集中参数得分 |
| random_state | 控制随机抽样数据集的随机性 |
| n_jobs | 设置工作时参与计算的线程数 |
| verbose | 输出工作日志形式 |
在sklearn当中,我们可以使用HalvingGridSearchCV类来实现对半网格搜索。Halving搜索是sklearn 1.0.1版本才新增的功能,因此现在该功能还处于实验阶段,在导入该类的时候需要同时导入用以开启对半网格搜索的辅助功能enable_halving_search_cv。当且仅当该功能被导入时,HalvingGridSearchCV才能够被导入和使用。
import re
import sklearn
import numpy as np
import pandas as pd
import matplotlib as mlp
import matplotlib.pyplot as plt
import time
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.experimental import enable_halving_search_cv
from sklearn.model_selection import KFold, HalvingGridSearchCV
param_grid_simple = {'n_estimators': [*range(5,100,5)]
, 'max_depth': [*range(25,36,2)]
, "max_features": ["log2","sqrt",16,32,64,"auto"]
}
#建立回归器、交叉验证
reg = RFR(random_state=1412,verbose=True,n_jobs=12)
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
"""
对半网格搜索(Halving Grid Search)参数的确定:
(需要多尝试)
factor = 1.3 # 每次变化量
n_samples = X.shape[0]
n_splits = 5
min_resources = 100 # 初始样本量
space = 342 # 这时param_grid_simple中每一项参数的个数乘积
for i in range(100):
if (min_resources*factor**i > n_samples) or (space/factor**i < 1):
break
print(i,"本轮迭代样本:{}".format(min_resources*factor**i)
,"本轮验证参数组合:{}".format(space//factor**i + 1))
# 通常最后一次剩下的情况不能太大或太小10~20就差不多了。
# 另外最后一次样本进行和训练集大小差不多
"""
#定义随机搜索
search = HalvingGridSearchCV(estimator=reg
,param_grid=param_grid_simple
,factor=1.3
,min_resources=100
,scoring = "neg_mean_squared_error"
,verbose = True
,random_state=1412
,cv = cv
,n_jobs=12)
start = time.time()
search.fit(X,y)
print(time.time() - start)
#查看最佳评估器
search.best_estimator_
"""
RandomForestRegressor(max_depth=31, max_features='sqrt', n_estimators=95,
n_jobs=12, random_state=1412, verbose=True)
"""
#查看最佳评估器
abs(search.best_score_)**0.5
# 30915.40250783341
1.2 贝叶斯超参数优化(推荐)
贝叶斯优化具有随机性,所以一定要注意random_state等随机因素的确定,保证结果的可复现性。
原理
首先,我们不理会HPO的问题,先来看待下面的例子。假设现在我们知道一个函数 f ( x ) f(x) f(x)的表达式以及其自变量 x x x的定义域,现在,我们希望求解出 x x x的取值范围上 f ( x ) f(x) f(x)的最小值,你打算如何求解这个最小值呢?面对这个问题,无论是从单纯的数学理论角度,还是从机器学习的角度,我们都已经见过好几个通俗的思路:
- 1 我们可以对 f ( x ) f(x) f(x)求导、令其一阶导数为0来求解其最小值
函数 f ( x ) f(x) f(x)可微,且微分方程可以直接被求解
- 2 我们可以通过梯度下降等优化方法迭代出 f ( x ) f(x) f(x)的最小值
函数 f ( x ) f(x) f(x)可微,且函数本身为凸函数
- 3 我们将全域的 x x x带入 f ( x ) f(x) f(x)计算出所有可能的结果,再找出最小值
函数 f ( x ) f(x) f(x)相对不复杂、自变量维度相对低、计算量可以承受
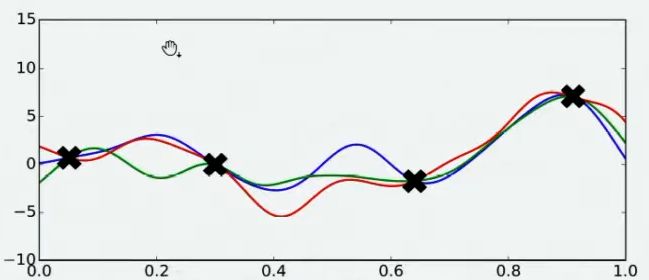
当我们知道函数 f ( x ) f(x) f(x)的表达式时,以上方法常常能够有效,但每个方法都有自己的前提条件。假设现在函数 f ( x ) f(x) f(x)是一个平滑均匀的函数,但它异常复杂、且不可微,我们无法使用上述三种方法中的任意一种方法求解,但我们还是想求解其最小值,可以怎么办呢?由于函数异常复杂,带入任意 x x x计算的所需的时间很长,所以我们不太可能将全域 x x x都带入进行计算,但我们还是可以从中随机抽样部分观测点来观察整个函数可能存在的趋势。于是我们选择在 x x x的定义域上随机选择了4个点,并将4个点带入 f ( x ) f(x) f(x)进行计算,得到了如下结果:
好了,现在有了这4个观测值,你能告诉我 f ( x ) f(x) f(x)的最小值在哪里吗?你认为最小值点可能在哪里呢?大部分人会倾向于认为,最小值点可能非常接近于已观测出4个 f ( x ) f(x) f(x)值中最小的那个值,但也有许多人不这么认为。当我们有了4个观测值,并且知道我们的函数时相对均匀、平滑的函数,那我们可能对函数的整体分布有如下猜测:
当我们对函数整体分布有一个猜测时,这个分布上一定会存在该函数的最小值。同时,不同的人可能对函数的整体分布有不同的猜测,不同猜测下对应的最小值也是不同的。
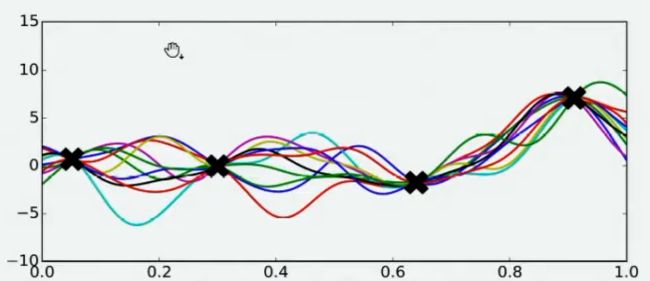
现在,假设我们邀请了数万个人对该问题做出猜测,每个人所猜测的曲线如下图所示。不难发现,在观测点的附近,每个人猜测的函数值差距不大,但是在远离远侧点的地方,每个人猜测的函数值就高度不一致了。这也是当然的,因为观测点之间函数的分布如何完全是未知的,并且该分布离观测点越远时,我们越不确定真正的函数值在哪里,因此人们猜测的函数值的范围非常巨大。
现在,我们将所有猜测求均值,并将任意均值周围的潜在函数值所在的区域用色块表示,可以得到一条所有人猜测的平均曲线。不难发现,色块所覆盖的范围其实就是大家猜测的函数值的上界和下界,而任意 x x x所对应的上下界差异越大,表示人们对函数上该位置的猜测值的越不确定。因此上下界差异可以衡量人们对该观测点的置信度,色块范围越大,置信度越低。
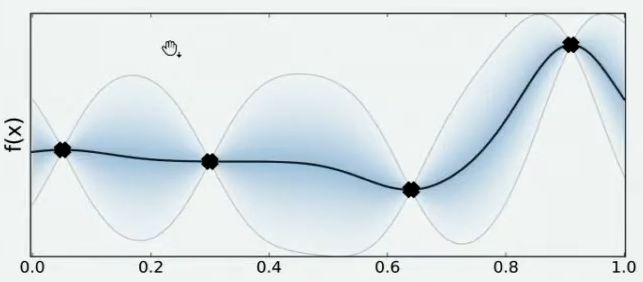
在观测点周围,置信度总是很高的,远离观测点的地方,置信度总是很低,所以如果我们能够在置信度很低的地方补充一个实际的观测点,我们就可以很快将众人的猜测统一起来。以下图为例,当我们在置信度很低的区间内取一个实际观测值时,围绕该区间的“猜测”会立刻变得集中,该区间内的置信度会大幅升高。
当整个函数上的置信度都非常高时,我们可以说我们得出了一条与真实的 f ( x ) f(x) f(x)曲线高度相似的曲线 f ∗ f^* f∗,次数我们就可以将 f ∗ f^* f∗的最小值当作真实 f ( x ) f(x) f(x)的最小值来看待。自然,如果估计越准确, f ∗ f^* f∗越接近 f ( x ) f(x) f(x),则 f ∗ f^* f∗的最小值也会越接近于 f ( x ) f(x) f(x)的真实最小值。那如何才能够让 f ∗ f^* f∗更接近 f ( x ) f(x) f(x)呢?根据我们刚才提升置信度的过程,很明显——观测点越多,我们估计出的曲线会越接近真实的 f ( x ) f(x) f(x)。然而,由于计算量有限,我们每次进行观测时都要非常谨慎地选择观测点。那现在,如何选择观测点才能够最大程度地帮助我们估计出 f ( x ) f(x) f(x)的最小值呢?
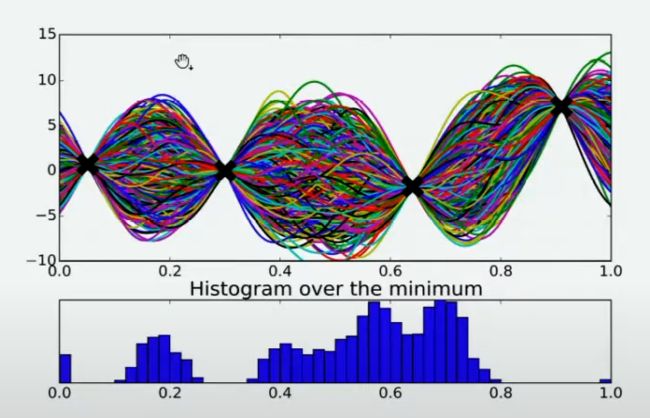
有非常多的方法,其中最简单的手段是使用最小值出现的频数进行判断。由于不同的人对函数的整体分布有不同的猜测,不同猜测下对应的最小值也是不同的,根据每个人猜测的函数结果,我们在 X X X轴上将定义域区间均匀划分为100个小区间,如果有某个猜测的最小值落在其中一个区间中,我们就对该区间进行计数(这个过程跟对离散型变量绘制直方图的过程完全一致)。当有数万个人进行猜测之后,我们同时也绘制了基于 X X X轴上不同区间的频数图,频数越高,说明猜测最小值在该区间内的人越多,反之则说明该猜测最小值在该区间内的人越少。该频数一定程度上反馈出最小值出现的概率,频数越高的区间,函数真正的最小值出现的概率越高。
当我们将 X X X轴上的区间划分得足够细后,绘制出的频数图可以变成概率密度曲线,曲线的最大值所对应的点是 f ( x ) f(x) f(x)的最小值的概率最高,因此很明显,我们应该将曲线最大值所对应的点确认为下一个观测点。根据图像,我们知道最小值最有可能在的区间就在x=0.7左右的位置。当我们不取新的观测点时,现在 f ( x ) f(x) f(x)上可以获得的可靠的最小值就是x=0.6时的点,但我们如果在x=0.7处取新的观测值,我们就很有可能找到比当前x=0.6的点还要小的 f m i n f_{min} fmin。因此,我们可以就此决定,在x=0.7处进行观测。
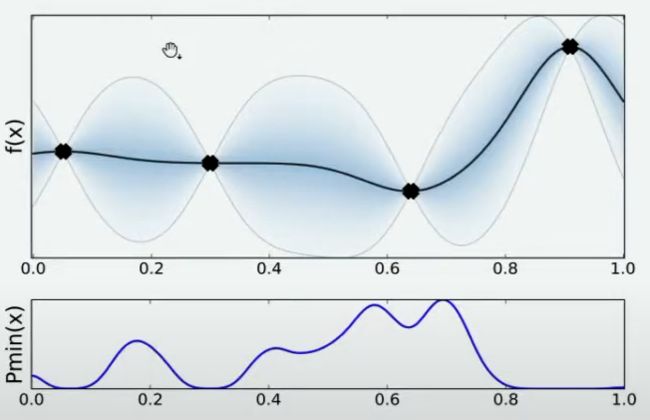
当我们在x=0.7处取出观测值之后,我们就有了5个已知的观测点。现在,我们再让数万人根据5个已知的观测点对整体函数分布进行猜测,猜测完毕之后再计算当前最小值频数最高的区间,然后再取新的观测点对 f ( x ) f(x) f(x)进行计算。当允许的计算次数被用完之后(比如,500次),整个估计也就停止了。
你发现了吗?在这个过程当中,我们其实在不断地优化我们对目标函数 f ( x ) f(x) f(x)的估计,虽然没有对 f ( x ) f(x) f(x)进行全部定义域上的计算,也没有找到最终确定一定是 f ( x ) f(x) f(x)分布的曲线,但是随着我们观测的点越来越多,我们对函数的估计是越来越准确的,因此也有越来越大的可能性可以估计出 f ( x ) f(x) f(x)真正的最小值。这个优化的过程,就是贝叶斯优化。
这个方法的基本思想还是通过计算一些点的情况,通过这些确定的点的情况判断附近的点的情况,将可能产生最小值得地方附近计算这里的模型值,通过这里的值进一步判断,(若我们计算了情况A,那么A附近的情况能大致模拟出来,离确定点越近判断结果越可靠,越远波动越大,越不可信。)
在贝叶斯优化的数学过程当中,我们需要有以下步骤:
- 定义需要估计的 f ( x ) f(x) f(x)以及 x x x的定义域。
- 取出有线的 N 个 x N个x N个x上的值,求出这些值对应的 f ( x ) f(x) f(x)也就是求出观测模型的预测值。
- 根据有限的观测值对于函数进行估计,该假设被称为贝叶斯优化中的先验假设,通过该估计 f ∗ f* f∗上的目标值最大值或最小值。
- 定义某种规则以确定下一个需要计算的的观测点。
并持续在 2 − 4 2-4 2−4 步中进行循环,直到假设分布上的目标值达到我们的标准,或者说所有计算资源被用完为止,例如最多观测 M M M 次或者最多运行 t t t 分钟。
![]()
以上流程又被称为序贯模型优化(SMBO),是最为经典的贝叶斯优化方法。在实际的运算过程当中,尤其是超参数优化的过程当中,有以下具体细节需要注意:
-
当贝叶斯优化不被用于HPO时,一般 f ( x ) f(x) f(x)可以是完全的黑盒函数(black box function,也译作黑箱函数,即只知道 x x x与 f ( x ) f(x) f(x)的对应关系,却丝毫不知道函数内部规律、同时也不能写出具体表达式的一类函数),因此贝叶斯优化也被认为是可以作用于黑盒函数估计的一类经典方法。但在HPO过程当中,需要定义的 f ( x ) f(x) f(x)一般是交叉验证的结果/损失函数的结果,而我们往往非常清楚损失函数的表达式,只是我们不了解损失函数内部的具体规律,因此HPO中的 f ( x ) f(x) f(x)不能算是严格意义上的黑盒函数。
-
在HPO中,自变量 x x x就是超参数空间。在上述二维图像表示中, x x x为一维的,但在实际进行优化时,超参数空间往往是高维且极度复杂的空间。
-
最初的观测值数量n、以及最终可以取到的最大观测数量m都是贝叶斯优化的超参数,最大观测数量m也决定了整个贝叶斯优化的迭代次数。
-
在第3步中,根据有限的观测值、对函数分布进行估计的工具被称为概率代理模型(Probability Surrogate model),毕竟在数学计算中我们并不能真的邀请数万人对我们的观测点进行连线。这些概率代理模型自带某些假设,他们可以根据廖廖数个观测点估计出目标函数的分布 f ∗ f^* f∗(包括 f ∗ f^* f∗上每个点的取值以及该点对应的置信度)。在实际使用时,概率代理模型往往是一些强大的算法,最常见的比如高斯过程、高斯混合模型等等。传统数学推导中往往使用高斯过程,但现在最普及的优化库中基本都默认使用基于高斯混合模型的TPE过程。
-
在第4步中用来确定下一个观测点的规则被称为采集函数(Aquisition Function),采集函数衡量观测点对拟合 f ∗ f^* f∗所产生的影响,并选取影响最大的点执行下一步观测,因此我们往往关注采集函数值最大的点。最常见的采集函数主要是概率增量PI(Probability of improvement,比如我们计算的频数)、期望增量(Expectation Improvement)、置信度上界(Upper Confidence Bound)、信息熵(Entropy)等等。上方gif图像当中展示了PI、UCB以及EI。其中大部分优化库中默认使用期望增量。
在HPO中使用贝叶斯优化时,我们常常会看见下面的图像,这张图像表现了贝叶斯优化的全部基本元素,我们的目标就是在采集函数指导下,让 f ∗ f^* f∗尽量接近 f ( x ) f(x) f(x)。
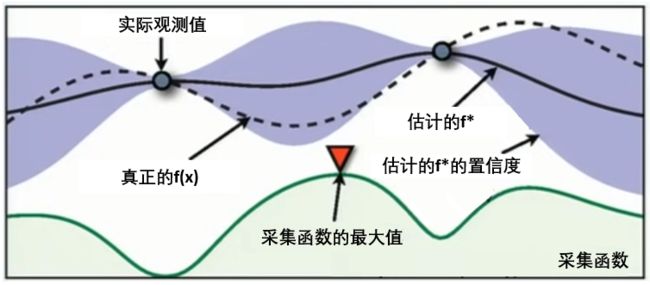
贝叶斯优化是当今黑盒函数估计领域最为先进和经典的方法,在同一套序贯模型下使用不同的代理模型以及采集函数、还可以发展出更多更先进的贝叶斯优化改进版算法,因此,贝叶斯优化的其算法本身就多如繁星,实现各种不同种类的贝叶斯优化的库也是琳琅满目,几乎任意一个专业用于超参数优化的工具库都会包含贝叶斯优化的内容。我们可以在以下页面找到大量可以实现贝叶斯优化方法的HPO库:https://www.automl.org/automl/hpo-packages/ ,其中大部分库都是由独立团队开发和维护,因此不同的库之间之间的优劣、性格、功能都有很大的差异。在课程中,我们将介绍如下三个可以实现贝叶斯优化的库:bayesian-optimization,hyperopt,optuna。
| HPO库 | 优劣评价 | 推荐指数 |
|---|---|---|
| bayes_opt | ✅实现基于高斯过程的贝叶斯优化 ✅当参数空间由大量连续型参数构成时 ⛔包含大量离散型参数时避免使用 ⛔算力/时间稀缺时避免使用 |
⭐⭐ |
| hyperopt | ✅实现基于TPE的贝叶斯优化 ✅支持各类提效工具 ✅进度条清晰,展示美观,较少怪异警告或报错 ✅可推广/拓展至深度学习领域 ⛔不支持基于高斯过程的贝叶斯优化 ⛔代码限制多、较为复杂,灵活性较差 |
⭐⭐⭐⭐ |
| optuna | ✅(可能需结合其他库)实现基于各类算法的贝叶斯优化 ✅代码最简洁,同时具备一定的灵活性 ✅可推广/拓展至深度学习领域 ⛔非关键性功能维护不佳,有怪异警告与报错 |
⭐⭐⭐⭐ |
1.2.1 BayesOpt实现高斯过程GP(较慢)
from bayes_opt import BayesianOptimization
这个开源比较早,代码简单,不过处理方式较为原始,缺乏阶的提效监控能力,对于算力要求比较高,但是当我们必须要实现基于高斯过程的贝叶斯优化算法的参数空间时并且带有大量的连续性参数时,我们才会考虑使用。
- 过程无法复现,结果可以
- 效率不足,无法提前停止,有时会出现训练相同的参数组合的情况
1.2.1.1 定义目标函数
就是我们首先需要定义一个函数我们给这个函数,一组超参数它会返回给我们该超参数下模型的效果,这个效果可以用损失或者得分来表示。但是有三个影响目标函数定义的规则。
- 目标函数的输入必须是具体的超参数而不能是整个超参数空间,更不能是数据算法等超三数以外的元素。
- 超参数的输入值只能是fud数不支持整数或字符串。
- 只支持寻找 f ( x ) f(x) f(x)最大值,不寻找最小值
通俗点说就是贝叶斯优化会通过这个函数进行判断该参数模型的优劣程度
def bayesopt_objective(n_estimators, max_depth, max_features, min_impurity_decrease):
# 定义评估器
# 需要调整的超参数等于目标函数的输入,不需要调整的超参数则直接等于固定值
# 默认参数输入一定是浮点数,因此需要套上int做强制类型转换成整数
reg = RFR(n_estimators=int(n_estimators),
max_depth=int(max_depth),
max_features=int(max_features),
min_impurity_decrease=min_impurity_decrease,
random_state=1412,
verbose=False,
n_jobs=-1)
# 定义损失的输出,5折交叉验证的结果,输出为负根均方误差(-RMSE)
# 注意,交叉验证需要使用数据,但是我们不能够让数据X,y成为目标函数的输入。
cv = KFold(n_splits=5, shuffle=True, random_state=1412)
validation_loss = cross_validate(reg, X, y,
scoring="neg_root_mean_squared_error",
cv=cv,
verbose=False,
n_jobs=-1,
error_score="raise"
# 如果交叉验证出错了。就会显示错误理由
)
# 交叉验证输出的评估指标是负均方误差,因此本来就是负的失误
# 目标函数可直接输出该损失的均值
return np.mean(validation_loss["test_score"])
1.2.1.2 定义参数空间
在任意超参数优化期中优化器中,将参数空格中的超参数组合作为备选组合,一组一组输入到算法中进行训练,在贝叶斯优化中,超参数组合会被输入到我们定义好的目标函数 f ( x ) f(x) f(x)中,在 b a y e s − o p t bayes-opt bayes−opt中我们使用字典方式来定义参数空间,其中参数的名称为键,参数的值为范围值(元组),范围均为双向闭区间。
就是我们网格搜索的范围
# 注意是元组
param_grid_simple = {
"n_estimators": (80, 100),
"max_depth": (10, 25),
"max_feature": (10, 20),
"min_impurity_decrease": (0, 1)
}
因为参数只支持参数,中间的上界和下界,不支持写步长等参数,所以会直接取闭区间任意的浮点数作为备选参数,因此在填入模型参数中是整数时,我们要强制类型转化成int类型。
1.2.1.3 定义优化目标函数和具体流程
在任意贝叶斯优化算法的实践过程中,一定都会有设计随机性的过程,例如随机抽取点作为观测点,随机抽取部分观测点进行采集函数的计算,在大部分的优化过程中,这种随机性无法控制。即使我们填写了随机种子,优化算法也不能够固定下来,因此我们可以尝试填写随机种子,但需要记住优化算法,每一次运行时都不会一样。
虽然优化算法无法被复现,但是优化算法得出来的最佳超参数结果确实可以复现的,只要优化完毕之后,可以从优化算法的实例化对象中取出最佳参数组合以及最佳分数,该最佳分数组合被输入到交叉验证中是一定可以复现其最佳分数的,如果没有复现,最佳分数则交叉,验证过程的随机种子设置存在问题或者优化算法迭代流程存在问题。
就是通过给定一个初始点量和迭代次数调用目标函数判断优劣程度并作出判断如何进行下一次迭代,最后返回最优值,实际上这部分不一定写成函数形式,不过函数形式好看。
# 定义优化目标函数和具体流程
def param_bayes_opt(param_grid_simple,init_points, n_iter):
# 定义优化器,先实例化优化器
opt = BayesianOptimization(f=bayes_objective, # 需要优化的目标函数
pbounds=param_grid_simple, # 备选参数空间
random_state=1412) # 随机种子,但是从根本上来说无法控制
# 使用优化器,记住bayes_opt只支持最大化
opt.maximize(init_points=init_points, # 抽取多少个初始观测值
n_iter=n_iter) # 一共观测/迭代次数
# 优化完成,取出最佳参数和最佳分数
params_best = opt.max["params"]
score_best = opt.max["target"]
# 打印最佳参数和最佳分数
print("\n", "\n", "best params :", params_best)
print("\n", "\n", "best cvscore :", score_best)
# 返回最佳参数和最佳分数
return params_best, score_best
1.2.1.4 验证(非必要)
我们刚才提到最优化方法的最优化参数可以被复现,所以我们定一个函数取出最优化结果观察我们的结果通过结果来判断是否存在问题。
就是将最有参数组复现出来,这个就特别简单
def bayes_opt_validation(params_best):
reg = RFR(n_estimators=int(params_best["n_estimators"]),
max_depth=int(params_best["max_depth"]),
max_features=int(params_best["max_features"]),
min_impurity_decrease=params_best["min_impurity_decrease"],
random_state=1412,
verbose=False,
n_jobs=-1)
cv = KFold(n_splits=5, shuffle=True, random_state=1412)
validation_loss = cross_validate(reg, X, y,
scoring="neg_root_mean_squared_error",
cv=cv,
verbose=False,
n_jobs=-1,
error_score="raise"
# 如果交叉验证出错了。就会显示错误理由
)
return np.mean(validation_loss["test_score"])
1.2.1.5 执行
import sklearn
import numpy as np
import pandas as pd
from sklearn.model_selection import KFold, cross_validate
from sklearn.ensemble import RandomForestRegressor as RFR
from bayes_opt import BayesianOptimization
import hyperopt
from hyperopt.early_stop import no_progress_loss
import optuna
data = pd.read_csv(
r"D:\学习资料\sklearn课件\AutoML与超参数优化——菜菜\train_encode.csv", index_col=0)
X = data.iloc[:, :-1]
y = data.iloc[:, -1]
start = time.time()
# 运行贝叶斯
params_best, score_best = param_bayes_opt(
param_grid_simple, 20, 280) # 初始化看了20个,观测值后面替代280次
# 记录并计算时间
print("训练时间:%s 分钟" % ((time.time()-start)/60))
# 验证模型结果
validation_score = bayes_opt_validation(params_best)
# 显示最优化模型参数结果
print("\n", "\n", "validation_score: ", validation_score)
"""
best params : {'max_depth': 22.754861061950113,
'max_features': 14.020522796997795,
'min_impurity_decrease': 0.0,
'n_estimators': 88.70408461644216}
best cvscore : -28385.755008050553
训练时间:7.725130772590637 分钟
validation_score: -28385.755008050553
"""
会显示迭代过程
![]()
1.2.2 hyperopt贝叶斯方法(推荐)
使用GBDT进行调参,先根据之前对数据的训练确定GBDT参数大致范围:
![]()
1.2.2.1 导包–导入数据–init初始学习器的建立
import sklearn
import numpy as np
import pandas as pd
from sklearn.model_selection import KFold, cross_validate
from sklearn.ensemble import RandomForestRegressor as RFR, GradientBoostingRegressor as GBR
import hyperopt
from hyperopt import hp, tpe, Trials, partial, fmin
from hyperopt.early_stop import no_progress_loss
import optuna
data = pd.read_csv(
r"D:\学习资料\sklearn课件\AutoML与超参数优化——菜菜\train_encode.csv", index_col=0)
X = data.iloc[:, :-1]
y = data.iloc[:, -1]
# init初始学习器的建立
rf = RFR(n_estimators=22, max_depth=22, max_features=14,
min_impurity_decrease=0, random_state=1412, verbose=False)
1.2.2.2 定义目标函数
# 这个和BayersOpt相同均是浮点数,若是整型数就要强制类型转换,若需要字符串或者浮点数就不用管
# params是特定的参数空间字典格式,在参数空间的确定会提到
# 若参数已经确定,就可直接填入参数
def hyperopt_objective(params):
reg = GBR(n_estimators=int(params["n_estimators"]),
learning_rate=params["learning_rate"],
criterion=params["criterion"],
loss=params["loss"],
max_depth=int(params["max_depth"]),
max_features=params["max_features"],
subsample=params["subsample"],
min_impurity_decrease=params["min_impurity_decrease"],
init=rf,
random_state=1412,
verbose=False)
cv = KFold(n_splits=5, shuffle=True, random_state=1412)
validation_loss = cross_validate(reg, X, y,
scoring="neg_root_mean_squared_error",
cv=cv,
verbose=False,
n_jobs=-1,
error_score="raise")
return np.mean(abs(validation_loss["test_score"]))# 这里和BayesOpt不同,这里使用了绝对值,因为hyperopt支持fmin,最小化
1.2.2.3 参数空间的确定
在任意超参数优化器中,优化器会将参数空格中的超参数组合作为备选组合,一组一组输入到算法中进行训练。在贝叶斯优化中,超参数组合会被输入我们定义好的目标函数 f ( x ) f(x) f(x)中。
在hyperopt中,我们使用特殊的字典形式来定义参数空间,其中键值对上的键可以任意设置,只要与目标函数中索引参数的键一致即可,键值对的值则是hyperopt独有的hp函数,包括了:
hp.quniform(“参数名称”, 下界, 上界, 步长) - 适用于均匀分布的浮点数
hp.uniform(“参数名称”,下界, 上界) - 适用于随机分布的浮点数
hp.randint(“参数名称”,上界) - 适用于[0,上界)的整数,区间为前闭后开
hp.choice(“参数名称”,[“字符串1”,“字符串2”,…]) - 适用于字符串类型,最优参数由索引表示
hp.choice(“参数名称”,[*range(下界,上界,步长)]) - 适用于整数型,最优参数由索引表示
hp.choice(“参数名称”,[整数1,整数2,整数3,…]) - 适用于整数型,最优参数由索引表示
hp.choice(“参数名称”,[“字符串1”,整数1,…]) - 适用于字符与整数混合,最优参数由索引表示
在hyperopt的说明当中,并未明确参数取值范围空间的开闭,根据实验,如无特殊说明,hp中的参数空间定义方法应当都为前闭后开区间。我们依然使用在随机森林上获得最高分的随机搜索的参数空间:
# 若是整数或者浮点数,并且是需要确定步长使用hp.quniform格式
# 若是字符串形式,用hp.choice格式数据
# hp.quniform("参数名", 起始位置, 结束位置, 步长)
# hp.choice("参数名",参数列表)
param_grid_simple = {'n_estimators': hp.quniform("n_estimators", 60, 140, 5),
"learning_rate": hp.quniform("learning_rate", 0.05, 1.05, 0.02),
"criterion": hp.choice("criterion", ["friedman_mse", "squared_error", "mse", "mae"]),
"loss": hp.choice("loss", ["squared_error"]),
"max_depth": hp.quniform("max_depth", 2, 12, 1),
"subsample": hp.quniform("subsample", 0.1, 0.6, 0.05),
"max_features": hp.choice("max_features", ["log2", "sqrt", 16, 17, 18, 19, 15, 14, "auto"]),
"min_impurity_decrease": hp.quniform("min_impurity_decrease", 0, 10, 0.5)
}
1.2.2.4 定义优化目标函数
def param_hyperopt(max_evals=100):
# 保存迭代过程的对象
trials = Trials()
# 设置提前停止,100次迭代,结果都没有减小就停止
early_stop_fn = no_progress_loss(100)
# 定义代理模型
params_best = fmin(hyperopt_objective, # 目标函数
space=param_grid_simple, # 参数空间
algo=tpe.suggest, # 最优化代理模型
max_evals=max_evals, # 最大迭代次数,默认100
verbose=True, # 显示过程
trials=trials, # 保存迭代过程
early_stop_fn=early_stop_fn # 设置提前停止
)
# 打印最优参数,fmin会自动打印最佳分数
print("\n", "\n", "best params: ", params_best, "\n")
# 返回最优参数和迭代过程
return params_best, trials
1.2.2.5 验证函数(非必要)
def hyperopt_validation(params):
reg = GBR(n_estimators=int(params["n_estimators"]),
learning_rate=params["learning_rate"],
criterion=params["criterion"],
loss=params["loss"],
max_depth=int(params["max_depth"]),
max_features=params["max_features"],
subsample=params["subsample"],
min_impurity_decrease=params["min_impurity_decrease"],
init=rf,
random_state=1412) # GBR中的random_state只能够控制特征抽样,不能控制样本抽样, verbose=False
cv = KFold(n_splits=5, shuffle=True, random_state=1412)
validation_loss = cross_validate(reg, x, y,
scoring="neg_root_mean_squared_error",
cv=cv,
verbose=False,
n_jobs=-1)
return np.mean(abs(validation_loss["test_score"]))
1.2.2.6 执行和建议
params_best,trials = param_hyperopt(100)
# 一般使用小于0.1%的空间进行训练
# 在多次调整模型参数范围时,获取最优参数值组时,若有些参数一直未发生变化,可能说明就是最优值,可以将对应参数值下的选项只保留最优的那一个,以缩小参数空间范围,提高效率
# 注意,在经过上面的调整后,需要将目标函数hyperopt_objective中的模型进行调整,将模型参数设置成固定的值
# 根据每一次结果调整参数范围,保证参数空间包含最优值
# 再确定范围后,可以进一步缩小参数空间范围,减小步长或增大迭代次数以确定更加精细的参数范围
结果:
#损失 best loss: 27549.81165947049
#最优参数:best params: {'criterion': 3, 'learning_rate': 0.14, 'loss': 0, 'max_depth': 7.0, 'max_features': 0, 'min_impurity_decrease': 3.5, 'n_estimators': 220.0, 'subsample': 0.5}
#注意:若之前定义参数空间使用的是hp.choice,那么最优参数中的取值为索引(主要是整型,定是索引)
# 将参数对应过后,调用验证函数 获取验证结果
hyperopt_validation({'criterion': "mae",
'learning_rate': 0.14,
'loss': "squared_error",
'max_depth': 7,
'max_features': "log2",
'min_impurity_decrease': 3.5,
'n_estimators': 220,
'subsample': 0.5})
# 27549.81165947049 和 之前一样
1.2.3 基于Optuna实现多种贝叶斯优化(推荐)
import optuna
1.2.3.1 定义目标函数与参数空间
Optuna的目标函数相当特别。在其他优化库中,我们需要单独输入参数或参数空间,优化器会在具体优化过程中将参数空间一一放入我们的目标函数进行优化,但在Optuna中,我们并不需要将参数或参数空间输入目标函数,而是需要直接在目标函数中定义参数空间。特别的是,Optuna优化器会生成一个指代备选参数的变量trial,该变量无法被用户获取或打开,但该变量在优化器中生存,并被输入目标函数。在目标函数中,我们可以通过变量trail所携带的方法来构造参数空间,具体如下所示:
def optuna_objective(trial):
#定义参数空间
n_estimators = trial.suggest_int("n_estimators",80,100,1) #整数型,(参数名称,下界,上界,步长)
max_depth = trial.suggest_int("max_depth",10,25,1)
max_features = trial.suggest_int("max_features",10,20,1)
#max_features = trial.suggest_categorical("max_features",["log2","sqrt","auto"]) #字符型
min_impurity_decrease = trial.suggest_int("min_impurity_decrease",0,5,1)
#min_impurity_decrease = trial.suggest_float("min_impurity_decrease",0,5,log=False) #浮点型
#定义评估器
#需要优化的参数由上述参数空间决定
#不需要优化的参数则直接填写具体值
reg = RFR(n_estimators = n_estimators
,max_depth = max_depth
,max_features = max_features
,min_impurity_decrease = min_impurity_decrease
,random_state=1412
,verbose=False
,n_jobs=-1
)
#交叉验证过程,输出负均方根误差(-RMSE)
#optuna同时支持最大化和最小化,因此如果输出-RMSE,则选择最大化
#如果选择输出RMSE,则选择最小化
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
validation_loss = cross_validate(reg,X,y
,scoring="neg_root_mean_squared_error"
,cv=cv #交叉验证模式
,verbose=False #是否打印进程
,n_jobs=-1 #线程数
,error_score='raise'
)
#最终输出RMSE,损失函数的最小值,需要在优化时最小化。
return np.mean(abs(validation_loss["test_score"]))
1.2.3.2 定义优化目标函数的具体流程
在HyperOpt当中我们可以调整参数algo来自定义用于执行贝叶斯优化的具体算法,在Optuna中我们也可以。大部分备选的算法都集中在Optuna的模块sampler中,包括我们熟悉的TPE优化、随机网格搜索以及其他各类更加高级的贝叶斯过程,对于Optuna.sampler中调出的类,我们也可以直接输入参数来设置初始观测值的数量、以及每次计算采集函数时所考虑的观测值量。在Optuna库中并没有集成实现高斯过程的方法,但我们可以从scikit-optimize里面导入高斯过程来作为optuna中的algo设置,而具体的高斯过程相关的参数则可以通过如下方法进行设置:
# n_trials表示迭代多少次
def optimizer_optuna(n_trials, algo):
#定义使用TPE或者GP(优化算法)
if algo == "TPE":
algo = optuna.samplers.TPESampler(n_startup_trials = 10 # 最开始有十个观测值
, n_ei_candidates = 24) # 每次计算采集函数时,随机采取24组参数组合进行预测
elif algo == "GP":
from optuna.integration import SkoptSampler # 使用关于optuna和其他包的混合库
import skopt # sklearn-optuna优化库
algo = SkoptSampler(skopt_kwargs={'base_estimator':'GP', #选择高斯过程
'n_initial_points':10, #初始观测点10个
'acq_func':'EI'} #选择的采集函数为EI,期望增量
)
#实际优化过程,首先实例化优化器
study = optuna.create_study(sampler = algo #要使用的具体算法
, direction="minimize" #优化的方向,可以填写minimize或maximize
)
#开始优化,n_trials为允许的最大迭代次数
#由于参数空间已经在目标函数中定义好,因此不需要输入参数空间
study.optimize(optuna_objective #目标函数
, n_trials=n_trials #最大迭代次数(包括最初的观测值的)
, show_progress_bar=True #要不要展示进度条呀?
)
#可直接从优化好的对象study中调用优化的结果
#打印最佳参数与最佳损失值
print("\n","\n","best params: ", study.best_trial.params,
"\n","\n","best score: ", study.best_trial.values,
"\n")
return study.best_trial.params, study.best_trial.values
1.2.3.3 执行实际优化流程
Optuna库虽然是当今最为成熟的HPO方法之一,但当参数空间较小时,Optuna库在迭代中容易出现抽样BUG,即Optuna会持续抽到曾经被抽到过的参数组合,并且持续报警告说"算法已在这个参数组合上检验过目标函数了"。在实际迭代过程中,一旦出现这个Bug,那当下的迭代就无用了,因为已经检验过的观测值不会对优化有任何的帮助,因此对损失的优化将会停止。如果出现该BUG,则可以增大参数空间的范围或密度。或者使用如下的代码令警告关闭:
import warnings
warnings.filterwarnings('ignore', message='The objective has been evaluated at this point before.')
optuna.logging.set_verbosity(optuna.logging.ERROR) #关闭自动打印的info,只显示进度条
best_params, best_score = optimizer_optuna(10,"TPE") #默认打印迭代过程
基于高斯过程的贝叶斯优化是比基于TPE的贝叶斯优化运行更加缓慢的.
结果求出后,可继续减小参数空间范围,增大参数密度,进一步优化目标参数组合
模型存储和读取
import joblib # 导入库函数
# 存储在本地文件,后缀dat,二进制文件
joblib.dump(xgb_model, "D:\\code_management\\xgb_model.dat")
# 读取文件
load_model = joblib.load("D:\\code_management\\xgb_model.dat")
感谢B站UP(菜菜的机器学习)