QEM网格简化算法
欢迎关注更多精彩
关注我,学习常用算法与数据结构,一题多解,降维打击。
qem 全称Quadic Error Metrics 网格简化。
它是一种基于二次度量误差的优化算法。
边塌缩算法
qem算法的基本思想是对某一边进行塌缩,将边的2点合成一个点,如下图。
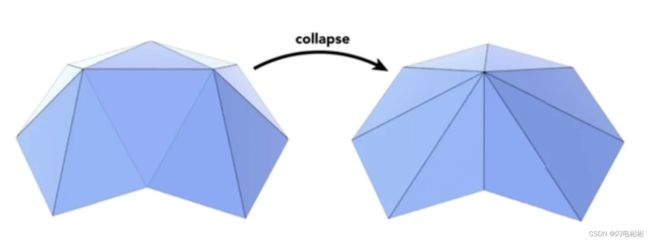
那么要选择哪条边进行塌缩呢。
就是基于二次度量误差。

上图表示。
假 设 p i , p j 点 边 塌 缩 前 的 端 点 , p x 为 塌 缩 后 的 点 坐 标 假设p_i,p_j点边塌缩前的端点,p_x为塌缩后的点坐标 假设pi,pj点边塌缩前的端点,px为塌缩后的点坐标
那 么 p x 需 要 到 p i , p i 各 邻 面 的 距 离 平 方 和 最 小 那么p_x需要到p_i,p_i 各邻面的距离平方和最小 那么px需要到pi,pi各邻面的距离平方和最小
能量如下:
E x = ∑ P s ∈ Ω ( i ) d ( p x , P s ) 2 + ∑ P s ∈ Ω ( j ) d ( p x , P s ) 2 E_x = \displaystyle \sum_{P_s \in \Omega(i)}d(p_x,P_s)^2 + \displaystyle \sum_{P_s \in \Omega(j)}d(p_x,P_s)^2 Ex=Ps∈Ω(i)∑d(px,Ps)2+Ps∈Ω(j)∑d(px,Ps)2
d ( p x , P s ) 代 表 p x 到 平 面 P s 的 垂 线 距 离 d(p_x, P_s) 代表p_x到平面P_s的垂线距离 d(px,Ps)代表px到平面Ps的垂线距离
只 要 向 量 p x 在 P s 法 向 上 的 投 影 减 去 平 面 上 一 点 在 法 向 上 的 投 影 即 可 只要向量p_x在P_s法向上的投影减去平面上一点在法向上的投影即可 只要向量px在Ps法向上的投影减去平面上一点在法向上的投影即可
由 于 p i 是 P s 上 一 点 由于p_i是P_s上一点 由于pi是Ps上一点
d ( p x , P s ) = p x ⋅ n s − p i ⋅ n s d(p_x, P_s)=p_x\cdot n_s-p_i\cdot n_s d(px,Ps)=px⋅ns−pi⋅ns
E x = ∑ P s ∈ Ω ( i ) ( p x ⋅ n s − p i ⋅ n s ) 2 + ∑ P s ∈ Ω ( j ) ( p x ⋅ n s − p j ⋅ n s ) 2 E_x = \displaystyle \sum_{P_s \in \Omega(i)}(p_x\cdot n_s-p_i\cdot n_s)^2 + \displaystyle \sum_{P_s \in \Omega(j)}(p_x\cdot n_s-p_j\cdot n_s)^2 Ex=Ps∈Ω(i)∑(px⋅ns−pi⋅ns)2+Ps∈Ω(j)∑(px⋅ns−pj⋅ns)2
优化上述方程使得E最小就可以得到px坐标。
从矩阵角度来求距离平方和

上 式 中 n i , − d i 都 是 常 量 , 所 以 Q i 也 是 常 上式中n_i, -d_i都是常量,所以Q_i也是常 上式中ni,−di都是常量,所以Qi也是常
再看上式
令 p x ‾ = ( p x , 1 ) 令\overline{p_x} = (p_x, 1) 令px=(px,1)
∑ P s ∈ Ω ( i ) d ( p x , P s ) 2 \displaystyle \sum_{P_s \in \Omega(i)}d(p_x,P_s)^2 Ps∈Ω(i)∑d(px,Ps)2
= ∑ P s ∈ Ω ( i ) p x ‾ T Q s p x ‾ =\displaystyle \sum_{P_s \in \Omega(i)}\overline{p_x}^TQ_s \overline{p_x} =Ps∈Ω(i)∑pxTQspx
= p x ‾ T [ ∑ P s ∈ Ω ( i ) Q s ] p x ‾ =\overline{p_x}^T\left[\displaystyle \sum_{P_s \in \Omega(i)}Q_s \right]\overline{p_x} =pxT⎣⎡Ps∈Ω(i)∑Qs⎦⎤px
从上述可以看出可以先对某点的总和计算。
Q t i = [ ∑ P s ∈ Ω ( i ) Q s ] Qt_i = \left[\displaystyle \sum_{P_s \in \Omega(i)}Q_s \right] Qti=⎣⎡Ps∈Ω(i)∑Qs⎦⎤
E x = p x ‾ T Q t i p x ‾ + p x ‾ T Q t j p x ‾ E_x=\overline{p_x}^TQt_i\overline{p_x}+\overline{p_x}^TQt_j\overline{p_x} Ex=pxTQtipx+pxTQtjpx
= p x ‾ T ( Q t i + Q t j ) p x ‾ =\overline{p_x}^T(Qt_i+Qt_j)\overline{p_x} =pxT(Qti+Qtj)px
可 以 看 出 上 只 有 p x 是 变 量 , 是 一 个 二 次 能 量 , 可 以 通 过 优 化 得 到 p x 最 优 解 , 即 为 塌 缩 后 的 点 坐 标 位 置 可以看出上只有p_x是变量,是一个二次能量,可以通过优化得到p_x最优解,即为塌缩后的点坐标位置 可以看出上只有px是变量,是一个二次能量,可以通过优化得到px最优解,即为塌缩后的点坐标位置
将 v 看 成 是 一 个 向 量 v = [ x , y , z , 1 ] , 并 展 开 得 到 下 式 , 然 后 进 行 求 导 , 并 可 以 得 到 A v = b 形 式 , 角 得 v = A − 1 b 将v看成是一个向量v=[x,y,z,1],并展开得到下式,然后进行求导,并可以得到Av=b形式, 角得v=A^{-1}b 将v看成是一个向量v=[x,y,z,1],并展开得到下式,然后进行求导,并可以得到Av=b形式,角得v=A−1b

算法步骤
for 所有点 i {
计算点能量总和Qti
}
for 所有边 x{
得到Ex, 并解出最优点px
}
while(点总数>目标值) {
先出Ex最小的边
将该边的两点从网格中删除。
将两点从网格中删除。
添加新的点。
连接受影响的点。
重新计算新边的能量。
}
代码实现
代码库
//
// Created by chenbinbin on 2022/5/9.
//
#include "hw9.h"
#include "../../PolyMesh/IOManager.h"
#include p = { a,b,c,d };
Q_temp += p * p.transpose();
}
Qv.insert(std::make_pair(vh, Q_temp));*/
}
///Initial Cost
for (MEdge* eh : mesh->edges())
{
State.insert(std::make_pair(eh, 0));
cal_Cost(eh);
}
/// simplification
int N_V = mesh->numVertices();
int target_num = std::min((int)(0.5*N_V), 1000);
while(N_V > target_num)
{
Edge_priority temp_edge = Cost.top();
Cost.pop();
MEdge* eh = temp_edge.eh;
if (temp_edge.state == State[eh])
{
if (eh->index() != -1)
{
if (QEM_collapse(temp_edge, mesh))
{
N_V--;
}
}
}
}
}
void qem_simplification()
{
char buffer[500];
getcwd(buffer, 500);
printf("The current directory is: %s/../\n", buffer);
string mesh_path = buffer;
mesh_path += "/../src/hw9/dragon.obj";
PolyMesh* mesh = new PolyMesh();
loadMesh(mesh_path, mesh);
// read input mesh
//PolyMesh* mesh = new PolyMesh();
//loadMesh("cat_open.obj", mesh);
clock_t start, end;
std::cout << "Begin QEM" << std::endl;
start = clock();
QEM(mesh);
end = clock();
std::cout << "time: " << (double)(end - start) / CLOCKS_PER_SEC << "s" << std::endl;
writeMesh("dragon-simplification-tri.obj", mesh);
}
效果展示
简化前
简化到20000点
简化10000点
简化到5000点
简化到2000点
简化到1000点
可以看到简化后网格数少了,基本形状还是维持得不错。
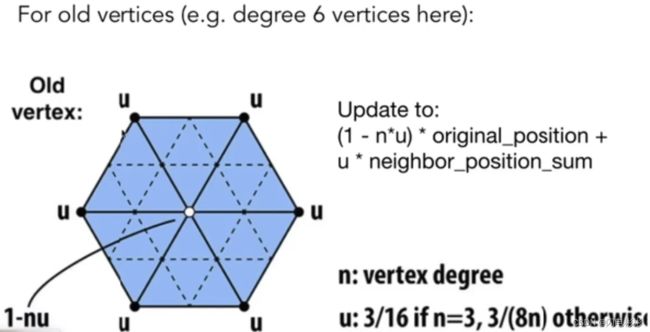
三角网格Loop细分
本人码农,希望通过自己的分享,让大家更容易学懂计算机知识。
![]()