三次样条(Cubic Spline)的C++实现以及可视化
无论是曲线拟合,能量优化还是分段函数模拟的应用中,通过一组离散点拟合出一条完整的曲线,都是不可避免的工作。一般来说,像贝塞尔曲线,b样条等曲线拟合方法,是通过控制点来生成曲线,控制点本身不经过曲线,这就带来一些不便。我们希望使用一种控制点在曲线上,同时保证曲线光滑,拟合结果良好方法,来实现曲线拟合。这就引出了我们今天的主题:三次样条曲线。
一. 背景知识
该部分参考博客:三次样条(cubic spline)插值 - 知乎
如果用一句话概括,三次样条就是有条件下的分段三次函数拟合问题。条件包括要通过特定的点序列以及保持函数的平滑。每一对相邻的点序列表示一个三次函数,每一个点是两个三次函数交汇处,代表起点和终点。平滑表示高阶导数具有连续性,基本表示到2阶。有了以上的了解,我们就能够对三次样条的求解进行数学建模:
1. 点序列{x0, x1, ...., xn}, 每一对点xm与xm+1之间会有一个对应的三次函数:Sm,且Sm(xm+1)=Sm+1(xm+1), 表示每一个点是两个三次函数的交汇。
2. 曲线光滑,即到二阶连续(S'').
根据端点设定不同的二阶约束,会产生不同的边界,包括自然边界,固定边界以及非节点边界。这里我们只使用自然边界的情况,即S''(x0)=S''(xn)=0。
具体推导,假设三次函数的参数为a,b,c,d,对应不同的次数,则能够得到:
这里我们不在展开推导过程,按照已知条件对上述方程进行变换,其问题转换为求解方程组:
其中h表示x的步长值,hm=xm+1-xm。m为求解中间变量。解上述线性方程,得到m的值。将m和h带入下面的方程,就得到了分段的三次函数表达式:(y是每一个已知点对应x的纵坐标)
到此,我们就得到了三次样条函数自然边界条件下的求解方法。
二. 程序实现
基于Eigen的C++程序实现,我参考的是以下两篇博客,分别介绍了Eigen的基础配置和HelloWorld程序以及对Ax=b的线性方程求解。
Eigen介绍:
C++矩阵处理工具——Eigen_Rachel Zhang的专栏-CSDN博客_c++ eigen
Eigen求解:
使用C++ Eigen库求解线性方程组Ax=b_Vitcharm的博客-CSDN博客_eigen 求解线性方程组
根据上面两篇博客的介绍,我写了一个类,来实现三次样条函数的C++程序实现,具体如下:
/*************************************************************
*
* CubicSpline
*
* 2021.12.14
*
*
* Function: Input discrete points and Output curve
* Points corss the curve.
*
*
*************************************************************/
#pragma once
#include
#include
//using Eigen::MatrixXd;
using namespace Eigen;
using namespace Eigen::internal;
using namespace Eigen::Architecture;
using namespace std;
class CubicSpline {
private:
vector> point2D;
vector> CubicSplineParameter;//a, b, c, d.
vector h;
vector m;
public:
void CubicSpline_init(vector> point2D_input) {
point2D = point2D_input;
//init h
h.clear();
h.resize(point2D.size() - 1);
for (int i = 0; i < point2D.size() - 1; i++) {
double x1 = point2D[i][0];
double x2 = point2D[i + 1][0];
double h_i = abs(x2 - x1);
h[i] = h_i;
}
//init m. m.size = point2D.size()
//1, compute yh coefficient
vector yh(point2D_input.size());
for (int i = 0; i < yh.size(); i++) {
if (i == 0 || i == yh.size() - 1) {
yh[i] = 0;
}
else {
yh[i] = 6 * ((point2D[i + 1][1] - point2D[i][1]) / h[i] - (point2D[i][1] - point2D[i - 1][1]) / h[i - 1]);
}
}
MatrixXf A(point2D.size(), point2D.size());
MatrixXf B(point2D.size(), 1);
MatrixXf m;
//2, init A, B
B(0, 0) = yh[0];
B(point2D.size() - 1, 0) = yh[point2D.size() - 1];
for (int i = 0; i < point2D.size() - 1; i++) {
A(0, i) = 0;
A(point2D.size() - 1, i) = 0;
}
A(0, 0) = 1;
A(point2D.size() - 1, point2D.size() - 2) = 1;
for (int i = 1; i < point2D.size() - 1; i++) {
B(i, 0) = yh[i];
for (int j = 0; j < point2D.size(); j++) {
if (j == i) {
A(i, j) = 2 * (h[i - 1] + h[i]);
}
else if (j == i - 1) {
A(i, j) = h[i - 1];
}
else if (j == i + 1) {
A(i, j) = h[i];
}
else {
A(i, j) = 0;
}
}
}
m = A.llt().solve(B);
vector mV(point2D.size());
for (int i = 0; i < point2D.size(); i++) {
mV[i] = m(i, 0);
}
for (int i = 0; i < m.size() - 1; i++) {
vector CubicSplineParameter_i;
double a = point2D[i][1];
double b = (point2D[i + 1][1] - point2D[i][1]) / h[i] - h[i] / 2 * mV[i] - h[i] / 6 * (mV[i + 1] - mV[i]);
double c = mV[i] / 2;
double d = (mV[i + 1] - mV[i]) / (6 * h[i]);
CubicSplineParameter_i.push_back(a);
CubicSplineParameter_i.push_back(b);
CubicSplineParameter_i.push_back(c);
CubicSplineParameter_i.push_back(d);
CubicSplineParameter.push_back(CubicSplineParameter_i);
}
}
vector> CubicSpline_Insert(int step) {
vector> insertList;
for (int i = 0; i < CubicSplineParameter.size(); i++) {
double h_i = h[i] / (double)step;
insertList.push_back(point2D[i]);
double a = CubicSplineParameter[i][0];
double b = CubicSplineParameter[i][1];
double c = CubicSplineParameter[i][2];
double d = CubicSplineParameter[i][3];
for (int j = 1; j < step; j++) {
double x_new = point2D[i][0] + h_i * j;
double y_new = a + b * (x_new - point2D[i][0])
+ c * (x_new - point2D[i][0]) * (x_new - point2D[i][0])
+ d * (x_new - point2D[i][0]) * (x_new - point2D[i][0]) * (x_new - point2D[i][0]);
vector p_new_ij;
p_new_ij.push_back(x_new);
p_new_ij.push_back(y_new);
insertList.push_back(p_new_ij);
}
}
insertList.push_back(point2D[point2D.size() - 1]);
return insertList;
}
vector> CubicSpline_Insert(double step) {
vector> insertList;
for (int i = 0; i < CubicSplineParameter.size(); i++) {
int h_i = h[i] / (double)step;
insertList.push_back(point2D[i]);
double a = CubicSplineParameter[i][0];
double b = CubicSplineParameter[i][1];
double c = CubicSplineParameter[i][2];
double d = CubicSplineParameter[i][3];
for (int j = 1; j < h_i; j++) {
double x_new = point2D[i][0] + step * j;
double y_new = a + b * (x_new - point2D[i][0])
+ c * (x_new - point2D[i][0]) * (x_new - point2D[i][0])
+ d * (x_new - point2D[i][0]) * (x_new - point2D[i][0]) * (x_new - point2D[i][0]);
vector p_new_ij;
p_new_ij.push_back(x_new);
p_new_ij.push_back(y_new);
insertList.push_back(p_new_ij);
}
}
insertList.push_back(point2D[point2D.size() - 1]);
return insertList;
}
};
调用的方法如下:
//存储已知的点序列
vector> pointList;
//初始化
CubicSpline cs;
cs.CubicSpline_init(pointList);
//输出样条插值后的结果,参数表示每一对点间要插入几个值
vector> pointInsert = cs.CubicSpline_Insert(10); 三. 可视化
上面的可视化是使用matplotlib-cpp生成。如果你希望使用该功能,请参考我之前的博客:
https://blog.csdn.net/aliexken/article/details/121673630.
通过程序实现,我们得到了插入新点之后的点序列。然后使用matplotlib-cpp的绘制功能,就能够得到一个最终的三次样条曲线拟合图,具体代码如下:
void PlotDraw_int(vector> plistOriginal, vector> plistInsert){
vector xO;
vector yO;
vector xI;
vector yI;
for (int i = 0; i < plistOriginal.size(); i++) {
xO.push_back(plistOriginal[i][0]);
yO.push_back(plistOriginal[i][1]);
}
for (int i = 0; i < plistInsert.size(); i++) {
xI.push_back(plistInsert[i][0]);
yI.push_back(plistInsert[i][1]);
}
// Plot line from given x and y data. Color is selected automatically.
plt::plot(xO, yO);
// Plot a red dashed line from given x and y data.
plt::plot(xI, yI, "r--");
// Add graph title
plt::title("Cubic Curves");
// Enable legend.
plt::legend();
// save figure
const char* filename = "basic.png";
std::cout << "Saving result to " << filename << std::endl;;
plt::save(filename);
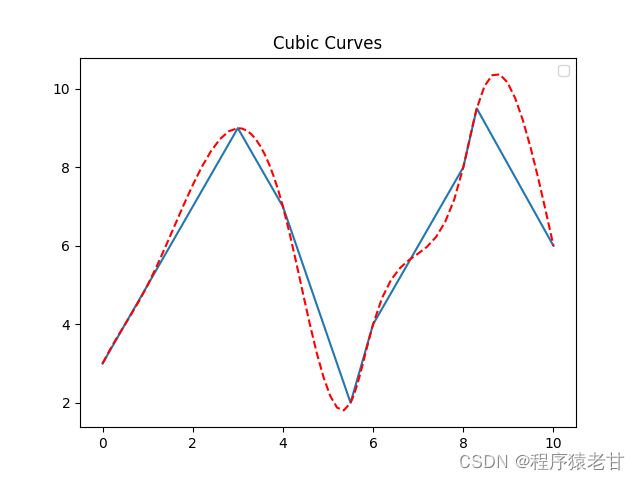
} 为了能够清楚的显示出插值前和插值后的区别,我将两个点序列的可视化都展现在图片中,其中plistOriginal表示插值前(对应上图蓝色折线),plistInsert表示插值后(对应上图红色虚线)。可以清楚的看到,插值后,曲线变得平滑。
总结
三次样条曲线具有非常重要的工程价值。我们在解很多拟合优化问题的时候,需要这种能够在有固定约束点的条件约束下,提供连续拟合的工具。最近一直在做的颜色迁移,就有这方面的应用。如果未来有机会的话,我会分享三次样条在颜色迁移方面的工程应用。如果您看到这里,希望可以点赞,分享我的文章,这对我的创作将大有助益。