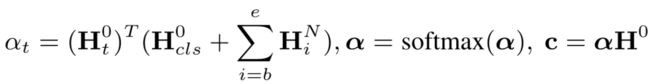Discrete Opinion Tree Induction for Aspect-based Sentiment Analysis 论文阅读笔记

一、作者

Chenhua Chen、Zhiyang Teng、Zhongqing Wang、Yue Zhang

School of Engineering, Westlake University, China

Institute of Advanced Technology, Westlake Institute for Advanced Study

Soochow University

二、背景

如何为每一个方面词定位相应的意见上下文是 ABSA 任务的关键挑战。最近的一些研究希望通过依赖树中的句法依赖来捕获方面和意见上下文之间的交互。事实上，尽管句法依赖能取得一定的效果，但它仍然会面临一些限制：首先，依赖解析器会在低资源域中表现地更差，甚至在面对低资源语言变得不可用；其次，依赖树通常情况下也不会针对方面情感分类来进行优化，一些现有的优化也只是针对节点分层，而没有优化依赖关系。

三、创新点

在本文中，作者提出了一个用于为每一个方面自动诱导离散意见树的模型。具体来说，该模型会从根节点开始，通过在当前节点的每一侧各选择一个子节点来构建树结构，并持续递归这个分割过程，以获得一个词汇化的二叉诱导树（induced tree），而后生成的诱导树将会作为输入被送到图卷积网络来训练情感分类器。

四、具体实现

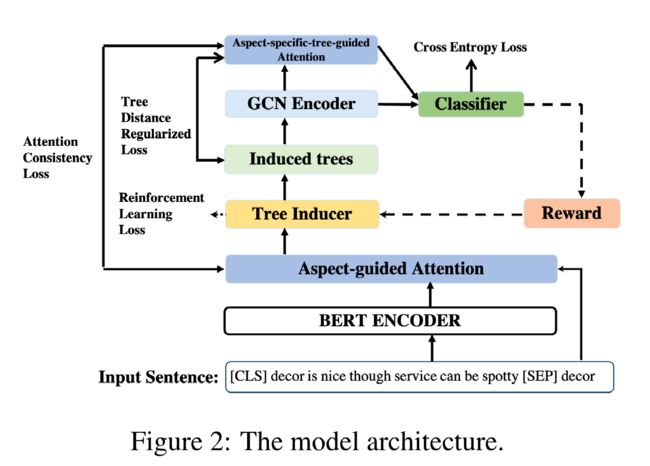
1.基于意见树的分类器

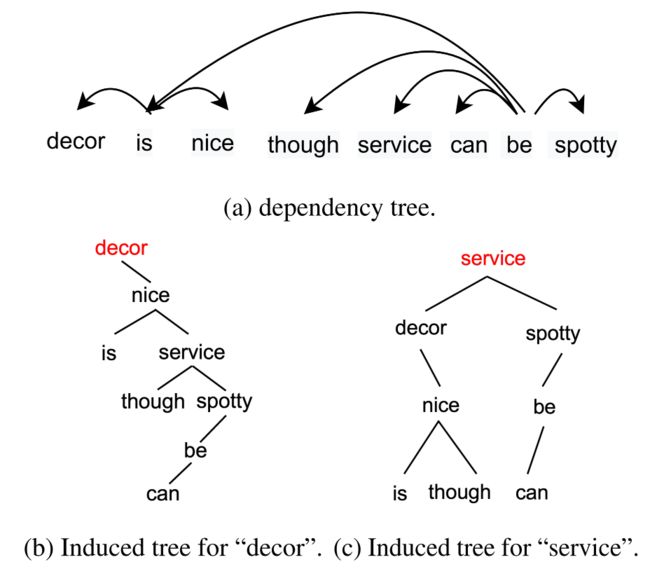
意见树将输入的句子表示为 $x=w_1{w}_2\dots w_n$，将方面表示为 $a=w_b{w}_{b+1}\dots w_e$，其中 $w_i$ 表示第 $i$ 个单词。对于每一棵意见树来说，二叉树的每一个节点都代表一个单词跨度，通过对二叉树进行中序遍历可以恢复原始句子，而在理想情况下根节点附近的节点应该包含相应的意见词。

下图中介绍了意见树生成算法的具体实现，其中 ${\mathbf{v}}_i^j$ 表示范围 $[i,j]$ 中单词对方面 $a$ 的极性 $y$ 贡献分数。算法首先将方面范围 $[b,e]$ 作为根节点，然后分别从方面词左右两侧选择得分最高的节点作为左右孩子节点，再然后通过递归调用构建函数来构造意见二叉树。其中，贡献分数的计算可以表示为 ${\mathbf{v}}^p={\mathbf{u}}_p\sigma ({\mathbf{W}}_p\mathbf{H}+{\mathbf{W}}_{a,p}{\mathbf{h}}_a)$，公式中的 $\sigma$ 代表 $\mathrm{ReLU}$ 激活函数，$\mathbf{H}$ 为通过将 $[\mathrm{CLS}]w_1{w}_2\dots w_n[\mathrm{SEP}]w_b{w}_{b+1}\dots w_e$ 输入 BERT 得到的方面特定的句子表示，${\mathbf{h}}_a$ 则表示通过将 ${\mathbf{H}}_b{\mathbf{H}}_{b+1}\dots {\mathbf{H}}_e$ 求和池化得到的方面表示。

基于生成的意见树 $t$ 和句子表示 $\mathbf{H}$，作者通过图卷积网络来学习每一个词的向量表示。首先，将意见树转化为一个无向图 $G$，该无向图的每一个节点表示一个单词，边通过邻接矩阵 $\mathbf{A}$ 来表示。邻接矩阵的构造规则如下：

基于邻接矩阵 $A$ 和第 $l-1$ 层的表示矩阵 ${\mathbf{H}}^{l-1}$，通过 GCNs 可以得到第 $l$ 层的表示 ${\mathbf{H}}^l=f(\mathbf{A}{\mathbf{H}}^{l-1}{\mathbf{W}}^l+{\mathbf{b}}^l)$，其中 $f$ 为激活函数，其余为模型参数，而 GCNs 第一层的输入 ${\mathbf{H}}^0$ 即为 BERT 给出的 $\mathbf{H}$。

基于 GCNs 的处理结果，最终的方面特定的特征表示 $\mathbf{c}$ 的计算如下图所示，其中 ${\alpha }_t$ 为方面 $a$ 对第 t 个单词的注意力分数。

基于最终的特征表示 $\mathbf{c}$，最终预测的情感分布为 $\mathbf{p}=\mathrm{softmax}({\mathbf{W}}_c\mathbf{c}+{\mathbf{b}}_c)$。

2.情感分类器的训练

情感分类器的训练通过最大化训练样本的对数似然来实现，训练的目标是最小化 ${\mathcal{L}}_{\sup }=-\sum _{i=1}^{|D|}\sum _{a\in x_i}\log {\mathbf{p}}_{i,y_a}$，其中 $|D|$ 为训练集的大小，$y_a$ 是第 i 个句子中的方面 a 的情感标签，${\mathbf{p}}_{i,y_a}$ 为上一步中得到的情感分布。

此外，作者认为靠近根节点的单词应该得到更高的注意力权重，给定意见树 t，作者计算了每个节点到根节点的最短路径，并通过 KL 散度函数来对注意力分数和正则化后的距离之间的关系进行协调。