Joint Extraction of Entities, Relations, and Events via Modeling Inter-Instance and Inter-Label论文解读

Joint Extraction of Entities, Relations, and Events via Modeling Inter-Instance and Inter-Label Dependencies

paper：2022.naacl-main.324.pdf (aclanthology.org)

code：暂时未公布

期刊/会议：NAACL 2022

摘要

事件触发词检测、实体提及识别、事件论元抽取和关系抽取是信息抽取中的四个重要任务，它们被联合执行(联合信息抽取- JointIE)，以避免错误传播并利用任务实例之间的依赖关系(即事件触发词、实体提及、关系和事件论元)。然而，以前的JointIE模型通常假设任务实例之间手工设计的启发式依赖关系和实例标签联合分布的平均场分解，因此无法捕获实例和标签之间的最佳依赖关系来提高表示学习和IE性能。为了克服这些限制，我们提出从数据中诱导任务实例之间的依赖关系图来促进表示学习。为了更好地捕获实例标签之间的依赖关系，我们建议通过条件随机场直接估计它们的联合分布。引入噪声对比估计来解决模型训练中难以处理的联合似然的最大化问题。最后，为了改进之前工作中的贪心搜索或束搜索的解码，我们提出了模拟退火，以便在解码时更好地找到实例标签的全局最优分配。实验结果表明，我们提出的模型在5个数据集和2种语言的多个IE任务上优于以前的模型。

1、简介

为了从非结构化文本中抽取结构化信息，典型的信息抽取(IE)管道涉及四个主要任务:事件触发词检测(ETD)、事件论元抽取(EAE)、实体提及识别(EMR)和关系抽取(RE)。之前的工作通过流水线方法执行了此类IE任务，其中一个任务的模型使用执行其他任务的其他模型的输出预测。因此，来自预测的错误可以在管道中的模型之间传播。

最近，ETD、EMR、EAE和RE在单一模型中联合求解，即联合信息提取- JointIE ，以避免错误传播，并利用四个IE任务(即句子中的事件触发词、实体提及、关系和事件论元候选)的预测实例之间的依赖关系。例如，如果提到的Person实体是Die事件的Victim论元，那么在同一句话中提到的同一实体很可能也是Attack事件的Target论元。为了隐式地利用实例依赖性进行表示学习，Wadden等人和Lin等人使用共享编码器来获取表示向量，以对不同IE任务的实例进行分类。后来的工作通过显式连接共享实体提及或事件触发词的任务实例或将共享文本范围的任务实例与语义图上的一些节点对齐，启发式地捕获IE任务实例之间的依赖关系，以帮助表示学习。虽然很自然，但这些任务实例之间依赖关系的手动设计对于JointIE的表示学习可能不是最优的。

除了表示学习之外，在预测级别，以前的工作倾向于将JointIE中所有任务实例的标签联合分布分解为每个单独实例的标签分布的乘积(即执行局部归一化)，从而阻碍了充分利用跨IE任务的实例标签交互的能力。Lin等人，Zhang和Ji通过使用手工制作的全局特征解码实例标签来缓解这一问题，而Nguyen等人则专注于通过全局类型依赖图上的一致性正则化来编码标签交互。然而，这些方法仍然假设对预测实例的联合标签分布进行因子分解，因此无法从根本上解决标签依赖编码问题。最近，一些工作试图通过使用最先进的预训练seq2seq模型(例如BART或T5)将JointIE任务重新定义为文本生成问题，从而直接模拟实例标签的联合分布。在这样的生成模型中，解码器以自回归的方式生成任务实例的文本范围和标签，以编码标签依赖性以进行联合分布计算。不幸的是，这种方法需要假设要解码的任务实例的顺序(例如，从左到右)，不允许后面的实例按照干扰/纠正先前实例的预测的顺序进行解码，从而导致JointIE的性能不佳。

在这项工作中，我们的目标是克服这些问题，通过从数据中诱导JointIE任务实例之间的依赖关系来促进表示学习，并直接建模所有任务实例的标签联合分布以完全支持标签交互。为此，我们将每个任务实例视为全连接依赖图中的一个节点;然后学习每条边的权重，以捕获两个对应实例之间的依赖关系级别。请注意，这与之前的工作不同，他们启发式地用不连接的任务实例对设计更稀疏的依赖关系图，因此无法探索实例对之间的所有可能交互以获得最佳表示。在我们的方法中，实例节点的诱导依赖图随后被图卷积网络(GCNs)使用，根据依赖级别，使用来自所有其他节点的信息来增强每个实例节点的表示。然后，利用增强的实例表示和诱导依赖图通过条件随机场(CRF)估计实例标签的联合分布。这一公式使我们能够通过噪声对比估计(NCE) 近似最大化ground-truth实例标签的难以处理的联合似然，这将最大化问题转化为区分真实标签和噪声标签的非线性逻辑回归。

最后，JointIE之前的工作使用了贪心搜索或beam search来解码实例标签，由于它们的贪婪性质，这不是最优的。在这项工作中，我们提出了一种通过模拟退火(SA)进行JointIE的新解码算法，该算法已被证明能够近似函数的全局最优。实验结果表明，我们提出的JointIE模型在5个数据集和2种语言的多个任务上具有较大的优势，显著优于以前的模型。

2、问题陈述

给出一个句子，ETD旨在基于预定义的事件类型集(例如“Attack”和“Transport”)预测事件触发词的文本跨度和事件类型。同样，EMR试图确定句子中实体提到的文本跨度和实体类型(例如，“Person”，“Organization”)。不同于前两个任务，EAE和RE涉及对一对对象的一次预测。给定一个事件触发词和一个实体提及，EAE旨在预测事件触发词提及的实体的论元角色(例如，“Victim”)。论元角色可以是“Not-an-argument”，表明所提到的实体不是触发词的论元。对于RE，任务的重点是对给定的实体提及对的关系分类(例如，“Work For”)。还有一种特殊类型“no -relation”，用于指定两个实体提及之间没有关系。因此，我们将预定义事件类型、实体类型、论元角色和关系类型的并集$C$称为信息类型(不包括“Not-an-argument”和“No-relation”)。

3、模型

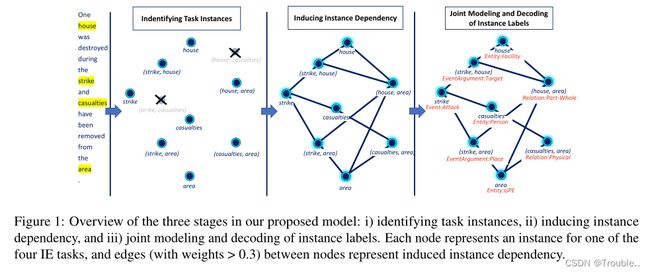
为了获取JointIE任务实例之间的依赖关系，一种方法是获取实体/事件提及候选对象的所有文本范围及其可能的对，以形成依赖关系图的节点，以改进表示学习。但是，这种方法将许多非实体/事件提及的文本片段保留下来，在建模中引入了噪声。它还会产生一个很大的依赖关系图，这会阻碍模型的效率。为此，我们的JointIE模型首先识别实体提及和事件触发词的文本跨度。然后，考虑所有可能的事件-实体对和实体-实体提及对，分别为事件论元和关系识别正样本对。被检测到的实体提及、事件触发词、事件论元和关系被称为任务实例，应该对它们进行分类，以便在$C$中获得相应的信息类型。在我们的模型中，将学习被检测到的任务实例之间的依赖关系图，为GCNs提供输入，以计算任务实例的依赖增强表示。最后，增强的表示将用于为所有任务实例计算标签上的联合分布，以训练我们的模型。我们还将使用模拟退火来实现解码阶段任务实例标签分配的全局最优。

3.1 识别事件和实体提及

对于一个输入句子$w=[w-1,...,w_N]$有$N$个单词，我们通过两个序列标注任务来识别事件触发词和实体提及。实际上我们使用BIO标签模式为$w$中的每个单词分配两个标签来标记事件触发词和实体提及的文本范围，即$\{\text{"B-TRIGGER"},\text{"I-TRIGGER"},\text{"O"}\}$标签用于事件触发词，$\{\text{"B-ENTITY"},\text{"I-ENTITY"},\text{"O"}\}$标签用于实体提及。首先利用基于transformer的预训练语言模型BERT 来获得句子中单词的上下文化嵌入:$X=x_1,...,x_N=BERT([w_1,...,w_N])$。

接下来，向量序列$X$被发送到两个不同的CRF层计算$w$中的事件触发词和事件提 及的标签序列的两种分布。然后得到触发词序列和实体标签序列的负对数似然$L_t$和$L_e$，并将其纳入整体训练损失中。在测试时，使用Viterbi算法确定$w$中事件触发词和事件提及的最佳标记序列。

设$V^t$和$V^e$分别为$w$中事件触发词和实体提及的文本跨度集(即训练时的正确跨度和测试时间的预测跨度)。为了准备下一个组件，我们分别计算每个事件触发词/实例$t_i\in V^t$和实体提及/实例$e_j\in V^e$的表示向量$z_i^t$和$z_j^e$，方法是对span内单词的上下文化嵌入进行平均。

3.2 识别事件论元和关系

给定检测到的事件触发词和实体提及，我们为每一对事件-实体提及$a_{ij}=(t_i,e_j)$(即，$t_i\in V^t,e_j\in V^e$)获得一个表示向量$z_{i,j}^a$，并为每一对实体-实体提及$r_{i,j}=(e_i,e_j)$(即，$e_i,e_j\in V^e$)获得一个表示向量$z_{i,j}^r$:$z_{i,j}^a=FF{N}_a^{down}(concat(z_i^t,z_j^e)),z_{i,j}^r=FF{N}_r^{down}(concat(z_i^e,z_j^e))$。

我们使用前向传播网络$FF{N}_a^{down}$和$FF{N}_r^{down}$，来确保$z_i^t,z_j^e,z_{ij}^a,z_{ij}^r$拥有相同的维度。接下来，将对表示向量$z_{ij}^a$和$z_{ij}^r$发送到两个不同的前馈网络，然后进行sigmoid激活，分别计算$a_{ij}$和$r_{ij}$作为事件论元和关系的正例的可能性:$p_{i,j}^a=\sigma (FF{N}^a(z_{ij}^a)),p_{i,j}^r=\sigma (FF{N}^r(z_{ij}^r))$。其中，$p_{ij}^a\in (0,1)$是实体提及$e_j$作为事件触发词$t_i$的实际论元的概率，而$p_{ij}^r\in (0,1)$是实体提及$e_i$和$e_j$之间存在关系的可能性。在训练时，我们获得事件论元和关系识别的负对数似然$L_a$和$L_r$，将其纳入总体损失函数进行最小化。在测试时，如果事件-实体对$a_{ij}$和实体-实体对$r_{ij}$的似然值$p_{ij}^a$和$p_{ij}^r$大于0.5，则保留它们作为事件论元和关系的正例。

为方便起见，设$V_a$和$V_r$分别为正样本事件-实体对$a_{ij}$(称为论元实例)和实体-实体对$r_{ij}$(称为关系实例)的集合。同时，设$V=V^t\cup V^e\cup V^a\cup V^r$为所有检测到的事件、实体、论元和关系实例的集合。对于每个实例$v_i\in V$，我们将使用$v_i$表示其对应的实例(即来自$z_i^t,z_j^e,z_{ij}^a,z_{ij}^r$)。

3.3 诱导实例依赖

给定$V$中检测到的事件、实体、论元和关系实例，仍然需要在$C$中预测实例的信息类型来解决JointIE。虽然可以直接使用实例表示$v_i$进行标签预测，但我们的目标是利用IE中的实例依赖关系，用来自其他实例的信息增强一个实例的表示向量，以促进类型预测。特别是，使用$V$中的实例$v_i$作为依赖关系图$G$中的节点，我们的目标是通过将实例提供给GCN模型来强化实例表示。因此，不是像以前的工作中那样假设实例之间的启发式手工设计的依赖关系图，我们建议自动学习$V$中的实例的依赖关系图$G$。为此，我们的依赖图$G$是$V$中节点之间的全连通图，其中每条边都学习了一个权值${\alpha }_{ij}\in (0,1)$，以量化$V$中实例$v_i$和$v_j$之间的依赖关系。在这项工作中，我们提出了两种信息源，可用于确定任务实例之间的依赖关系:(i)语义信息和(ii)语法信息。

语义信息：$v_i$和$v_j$之间边缘的语义权重${\alpha }_{ij}^{sem}$基于语义信息量化了它们之间的相关性/依赖性，即通过表示向量$v_i$和$v_j$: ${\alpha }_{ij}^{sem}=FF{N}^{sem}(concat(v_i,v_j))$。$FF{N}^{sem}$是一个前向神经网络，以sigmoid激活函数结尾。

语法信息：$v_i$和$v_j$之间边缘的基于句法的权值${\alpha }_{ij}^{syn}$的计算方法与${\alpha }_{ij}^{sem}$相似。特别地，对于每个词$w_k\in w$，我们在$w$的依赖树中检索$w_k$与其调控器之间的依赖关系$d_k$，该依赖树是由Trankit的依赖解析器生成的。然后，通过查找可学习依赖项嵌入矩阵$m$，得到$d_k$对$w_k$的嵌入$m_k$。然后，通过:$u_i=max-poo{l}_{wk\in SPA{N}_{vi}}(m_k)$计算实例$v_i\in V$的基于语法的表示向量$u_i$。这里，如果$v_i$是事件触发词或实体提及实例，$SPA{N}_{v_i}$在$w$中涉及到$v_i$对应的文本跨度中的单词。否则，$SPA{N}_{v_i}$包含了$v_i$对中涉及事件触发词和实体提及的文本范围内的单词。因此，我们通过${\alpha }_{ij}^{syn}=FF{N}^{syn}(concat(u_i,u_j))$计算$v_i$，$v_j$的基于语法的依赖权值${\alpha }_{ij}^{syn}$，其中$FF{N}^{syn}$也是一个具有sigmoid函数的前馈网络。最后，结合基于语义和句法的权重，得到$V$中$v_i$和$v_j$的总体依赖权重${\alpha }_{ij}$：${\alpha }_{ij}=({\alpha }_{ij}^{sem}+{\alpha }_{ij}^{syn})/2$。

3.4 使用GCNs强化表示

为了增强实例$v_i\in V$的表示向量，在诱导依赖图$G$上应用具有$K$层的GCN模型来计算实例的更强化的表示:
$$h_i^k=ReLU(\frac{{\sum }_{v_j\in V}{\alpha }_{ij}{W}^k{h}_j^{k-1}+b^k}{{\sum }_{v_j\in V}{\alpha }_{ij}}),1\le k\le K$$
其中$h_i^k$为GCN第$k$层实例$v_i$的表示($h{i}^0\equiv v_i$)， $W^k$、$b^k$为该层的可训练权值和偏差。

通过这种方式，来自所有其他实例$v_j(j\ne i)$的表示信息将根据它们学习到的依赖项权重合并到$v_i$的增强表示向量中。最后，使用最后一层的表示$h_i^K\equiv h_i$(为了简单起见，我们省略了$K$)来计算$v_i$的分数向量$s_i\in {\mathbb{R}}^{|C|}$，其中$s_i[C]$度量$v_i$在标签集$C$中拥有第$C$个标签的可能性:$s_i=FF{N}^{score}(h_i)$ ($FF{N}^{score}$是一个评分前馈网络)。分数向量$s_i$稍后将用于模拟$V$中所有实例的标签的联合分布。

3.5 计算标签的联合分布

设$Y$是$V$中实例$v_i$的标签$y_i$的集合。为了推断$V$中实例的标签，我们需要估计联合分布$P(Y|w,V)$。在之前的工作中， JointIE方法主要专注于学习任务实例的表示，以计算每个实例$v_i$的标签分布，用于预测:$P(y_i|w,V):=softmax(s_i)$。这种做法本质上意味着对$P(Y|w,V)$进行以下因式分解:$P(Y|w,V)={\prod }_{y_i\in Y}P(y_i|w,V)$。因此，这种分解假设实例标签的独立性，因此无法完全捕获IE任务的有用的标签依赖关系。

为了解决这个问题，我们直接估计联合分布$P(Y|w,V)$，这样可以促进实例标签之间的依赖关系，从而提高预测性能。为此，我们用条件随机场制定了联合分布$P(Y|w,V)$:
$$P(Y|w,V)=\frac{1}{Z(V)}\prod _{(v_i,v_j)}{\psi }_{ij}(y_i,y_j,V)$$
${\psi }_{ij}(y_i,y_j,V)$是定义在依赖图$G$边缘$(v_i,v_j)$上的positive potential function，且$Z(V)={\sum }_{Y^{\prime }\in C_V}{\prod }_{(v_i,v_j)}{\psi }_{ij}(y_i^{\prime },y_j^{\prime },V)$是保证$P(Y|w,V)$是一个有效概率分布($C_V$是$V$中实例的所有可能的标签分配$Y$的集合)的归一项。考虑到实例信息、实例依赖关系和标签依赖关系，我们提出potential function为:
$${\psi }_{ij}(y_i,y_j,V):=exp(s_i[y_i]+s_j[y_j]+{\alpha }_{ij}{\pi }_{y_i\leftrightarrow y_j})$$
其中$s_i[y_i]$是局部分数，例如$v_i$用标签$y_i$赋值，${\alpha }_{ij}$是$G$中边$(v_i,v_j)$的诱导依赖权值，${\pi }_{y_i\leftrightarrow y_j}$是可学习的转发分数(transit score)，表示标签$y_i$和$y_j$之间的依赖关系。根据这个公式，我们可以得到联合分布$P(Y|w,V)$:
$$P(Y|w,V)=\frac{exp(s(Y))}{{\sum }_{Y^{\prime }\in C_V}exp(s(Y^{\prime }))}$$

$$s(Y)=\gamma \sum _{v_i\in V}{s}_i[y_i]+\sum _{(v_i,v_j)}{\alpha }_{ij}{\pi }_{y_i\leftrightarrow y_j}$$

是实例的标签分配/配置$Y$的全局得分。$\gamma$是一个超参数，用来平衡局部分数(local score)和转发分数(transit score)。

为了训练模型，我们需要最大化公式(4)中正确标签配置$Y^{\ast }$的联合似然。然而，这需要计算归一化项${\sum }_{Y^{\prime }\in C_V}exp(s(Y^{\prime }))$，这是难以处理的。为了克服这个问题，我们采用了噪声对比估计(NCE)。NCE将最大化问题转化为区分正确标签配置和噪声标签配置的非线性逻辑回归。特别地，$P(Y^{\ast }|w,V)$的最大化是用NCE通过使对比损失最小化来实现的:
$$L_{NC}=-log\sigma (s(Y^{\ast }))-\sum _{n=1}^{N_{noi}}{E}_{y_n^{\prime }\sim P_{noi}}[log\sigma (-s(Y_n^{\prime }))]$$
$\sigma$是sigmoid激活函数，$N_{noi}$是由$P_{noi}$得出的噪声构型$Y_n^{\prime }$的数量，假设为均匀分布。直观地说，$L_{NC}$的最小化增加了真实标签配置$Y^{\ast }$的全局分数$s(Y^{\ast })$，同时降低了噪声标签配置$Y^{\prime }$的全局分数$s(Y^{\prime })$，以适当地训练模型。最后，训练我们模型的总体损失函数为:$L=L_t+L_e+L_a+L_r+L_{NC}$。

3.6 模拟退火联合解码

在推理时，我们需要搜索$C_V$中全局得分$s(\hat{Y})$最高的配置$\hat{Y}$:$\hat{Y}=argma{x}_{Y^{\prime }\in C_V}s(Y^{\prime })$。由于搜索空间$C_V$呈指数级增长($|C_V|=|C{|}^{|V|}$)，因此无法对$\hat{Y}$进行暴力搜索。以前的工作已经做了几次尝试来处理这个问题。Wadden和Nguyen只是对每个实例标签单独执行贪心解码，因此无法利用标签依赖性。Lin和Zhang采用beam search，通过扩展初始空赋值，逐步为$V$中的实例构造完整的解码赋值$Y$。每一步都对应于$V$中的一个实例，其中仅考虑该实例的顶级候选标签进行赋值扩展，并且仅为下一步保留到目前为止生成的顶级部分赋值。不幸的是，在每个步骤中选择用于扩展的最佳候选标签仅基于本地分数$s_i$，这可能会丢弃最终可以提供更大全局分数的候选标签。为了克服这个问题，我们建议应用模拟退火(SA) (Kirkpatrick et al, 1983)来搜索$V$的最优赋值$\hat{Y}$。SA是一种概率算法，能够近似地找到一个函数的全局最优值。算法1给出了SA查找$\hat{Y}$的实现。

算法的输入是初始配置${\hat{Y}}_{cur}={\hat{Y}}_0=\{{\hat{y}}_{i,0}\}$，其中包含每个实例的贪婪预测标签:${\hat{y}}_{i,0}=argma{x}_{c\in C}{s}_i[c]$。然后，该算法在$N_{iter}$迭代中运行，以提高当前标签配置${\hat{Y}}_{cur}$的全局得分$s({\hat{Y}}_{cur})$。这是通过将当前配置更新为后继配置${\hat{Y}}_{new}$来实现的，后者给出了更高的全局得分(即${\delta }_n>0$)。后继配置是通过函数$random\_successor()$通过随机更改一些标签$y_i\in {\hat{Y}}_{cur}$来获得的。与局部赋值的波束搜索解码不同，SA中的每个搜索步骤都检查$V$中实例的一个完整的标签赋值，以提供完整的信息来衡量赋值的全局分数/质量。重要的是，SA有时允许当前配置转移到全局得分较低的后续配置(即${\delta }_n\le 0$)，接受概率为$p=exp({\delta }_n/t)$。其中，$t$为算法的温度，通过$t\leftarrow T/n$逐渐降低($T$为超参数)。这种探索属性使SA能够逃避局部最优配置，从而增加了找到全局最优配置的机会。

4、实验

数据集：

• ACE数据集：ACE05-R，ACE05-E，ACE-E+
• ERE数据集：ERE-EN，ERE-ES

baseline：

• 生成式Baseline：Text2event、DEGREE
• 分类式Baseline：OneIE、AMRIE、FourIE

超参数设置：JointIE之前的工作采用了两种不同版本的预训练语言模型(PLM)，即BERT 和RoBERTa，这可能会导致不相容的情况。为此，我们探索BERT和RoBERTa，以获得GraphIE的单词表示$x_i$，以便进行公平的比较。对于西班牙ERE-ES数据集，在之前的工作之后，我们利用BERT和RoBERTa的多语言版本。对于每个PLM，我们在开发数据上微调GraphIE的超参数。

特别地，本文给出了所提模型超参数的最佳值。我们使用基于BERT的PLM模型(即使用bert-large- cases和bert-multilingual- cases)的学习率为1e−5，使用基于roberta的PLM(即使用roberta-large和xlm-roberta-large)的学习率为5e−6。对于其他超参数，我们的调优过程会在基于BERT的模型和基于RoBERT的模型中得到相同的值:Adam优化器,batch_size为10,依赖关系嵌入为100,前馈网络隐藏层的大小为400,GCN模型隐藏层的大小为200,前卫神经网络和GCN的层数为2,$\gamma =1$的权衡hyper-parameter全局得分,$N_{noi}=5$噪音对比的例子的数量损失(我们re-sample噪音例子每个时代),$T=5$表示初始温度，$N_{iter}=50$表示模拟退火(SA)的迭代次数，$\epsilon =0.1$表示SA解码的温度阈值。

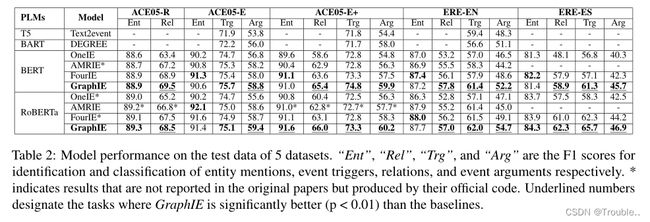
对比其他的Baseline：实验结果如下表2所示.

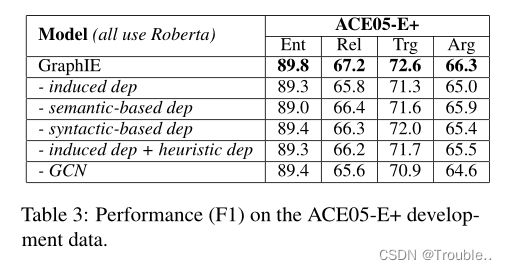
消融实验：在ACE05-E+数据集上进行消融实验，对比各部分的重要性。如表3所示。

在表4中，我们首先从GraphIE中消除了联合标签分布$P(Y|w,V)$的计算。因此，“-联合分布”模型使用局部标签分布$P(y_i|w,V)$来训练模型和推断标签(贪心解码)。由于“-联合分布”的效果明显较差，显然直接估计联合标签分布对JointIE是有帮助的。为了评估所提出的SA的效益，我们将其替换为GraphIE的其他解码算法，包括贪心搜索、beam search和hill climbing。beam search是用我们的全局评分函数$s(Y)$实现的，并遵循，而通过去除算法1的第11-12行中的配置探索来实现hill climbing。如表4所述，SA在GraphIE的解码算法中表现得比其他解码算法好得多，从而证明了SA在全局最优标签查找方面的能力。此外，我们还尝试将OneIE和AMRIE中的beam search解码替换为SA，这确实会导致这类模型的性能变差，如表4的后四行所示。我们将此归因于OneIE和AMRIE中配置的全局分数的学习，这涉及到有限的预定义全局特性集。许多可能的赋值$Y$对$V$不存在这样的特征，导致全局得分计算很差，阻碍了SA急需的配置排序。

分析：为了进一步理解GraphIE相对于基线模型的优势，我们手动分析了ACE05-E+开发数据上的实例，其中GraphIE可以做出正确的预测，但最好的基线模型FourIE失败了。图2展示了依赖关系图中的一些实例及其边和权重。从我们的分析中得到的最重要的见解是，GraphIE能够将依赖关系图中的实例(例如，blow)与其他支持实例(例如，suicide)连接起来，以提供重要的信息来促进正确的预测。这些支持实例不与当前实例共享任何事件触发词或实体，不能在FourIE中建立链接并导致失败预测。

最后，表5给出了由GraphIE对ACE05-E+中的某些标签对学习到的${\pi }_{y_i\leftrightarrow y_j}$转换分数。该表表明，我们的模型能够学习相关标签对的高分(例如，执行和句子事件类型)，而不相关标签对的低分(例如，传输事件的论元不能扮演攻击者的角色)。

5、相关工作

捕获IE任务之间的依赖关系一直是联合IE之前工作的主要焦点。早期的工作采用了特征工程方法。后来的工作通过共享参数应用深度学习来促进IE的联合建模，然而，只有两到三个任务的联合。最近，四个IE任务已经联合解决。然而，最近的研究仅采用启发式方法为实例手动设计依赖关系图。在先前的工作中，JointIE实例的联合标签分布的Mean-field factorization占主导地位。

我们的工作也与之前使用CRF的工作有关来估计实例标签的联合分布。序列标记是CRF解决的一个典型问题，包括词性标记和命名实体识别。然而，这些先前的工作仅将CRF用于简单的图结构(即线性链)。之前的一些工作已经考虑了更复杂的图结构的CRF;然而，这些作品都没有像我们一样为JointIE应用CRF。

6、总结

我们提出了一个联合解决四个IE任务(EMR, ETD, EAE和RE)的新模型。我们提出的模型通过一种新的边缘加权机制来学习任务位置之间的依赖关系图。我们还估计了实例标签之间的联合分布，以完全支持实例标签之间的交互，从而提高性能。实验结果表明，我们的模型在5个数据集和2种语言的多个JointIE任务中获得了最佳性能。在未来，我们计划扩展我们的方法，以涵盖更多的IE任务，如事件共指消解。