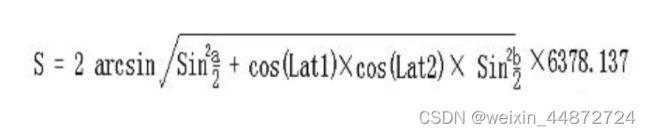真实地图最短路径规划(A*算法)
本文将研究矢量地图以及A*算法等系统关键的技术支持。在实现的过程中,还引入了高德出行API、聚焦类爬虫、OpenStreetMap开源地图,二叉堆等技术。
通过解析OpenStreetMap提供的地图数据,获取不同类型的交通路网信息。然后将A*算法应用于路网数据中,并引入真实地理距离作为矢量地图的参数权重。最终找到两地之间的最短路径方案,成功的实现预期目标。
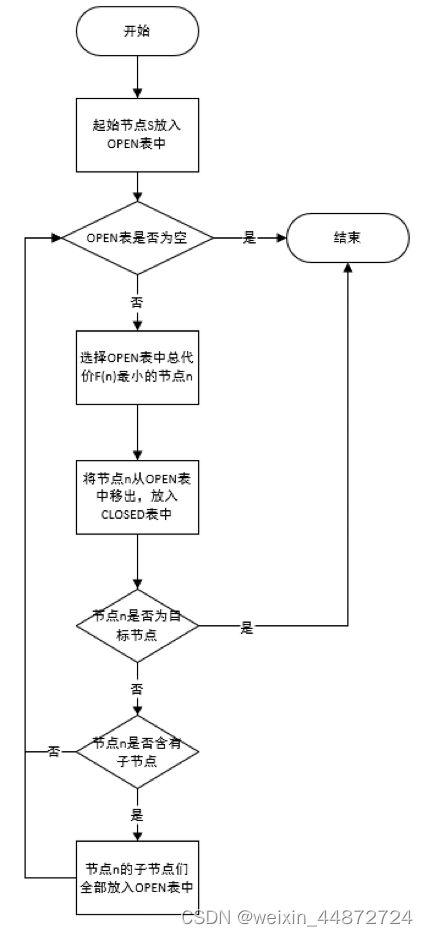
流程:
-
获取地图数据/路网数据化存储
-
不同路网数据获取(公共交通,机动车,自行车道,人行道....)
-
应用A*算法于地图中
地图路径规划的本质是遍历地图中的所有节点,然后找到最短路径的过程[8]。算法中的图是由大量节点和连接节点之间的线组成的。这里说的节点指的是现实生活中的每一个分叉路口,只要出现需要选择方向的时候,在地图上呈现的就是一个节点(vertices)[14]。而连接节点的线则是指现实生活中的道路,例如上海的南京西路,它在地图上的数据身份是一个边(edge)。每一条边都带有相对应的权重,即现实世界中的物理距离。图拥有两种类型,即有向图和无向图。有向图指的是带有方向的边,即a指向b的边和b指向a的边是两种不同的边。这两条边,在无向图中则是同一条边。
根据周小镜的描述,最短路径算法的基础是将图中的节点遍历[8]。由于实际路网的复杂性,节点的遍历有可能会出现从某一顶点选择一条边搜索后,该边又与带有该顶点的另一条边相交[8]。从而导致该顶点的重复遍历。因此在遍历地图的过程中,需要对已访问过的节点进行标记,以防重复遍历的出现[8]。
A*算法的关键在于启发函数,即F(n)=G(n)+H(n)。F(n)指代起始节点到目标节点的总代价。G(n)表示当前节点n到起始节点的当前代价。H(n)则表示当前节点n到目标节点的预估代价。依据这个函数,从而使得每一个被搜索的节点n都有一个总代价F(n)。然后选择其中最小的总代价节点作为下一步节点。接着继续计算新加入的节点的F(n),如此,循环。
1.获取地图数据/路网数据化存储
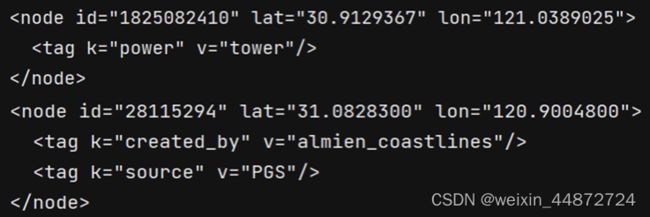
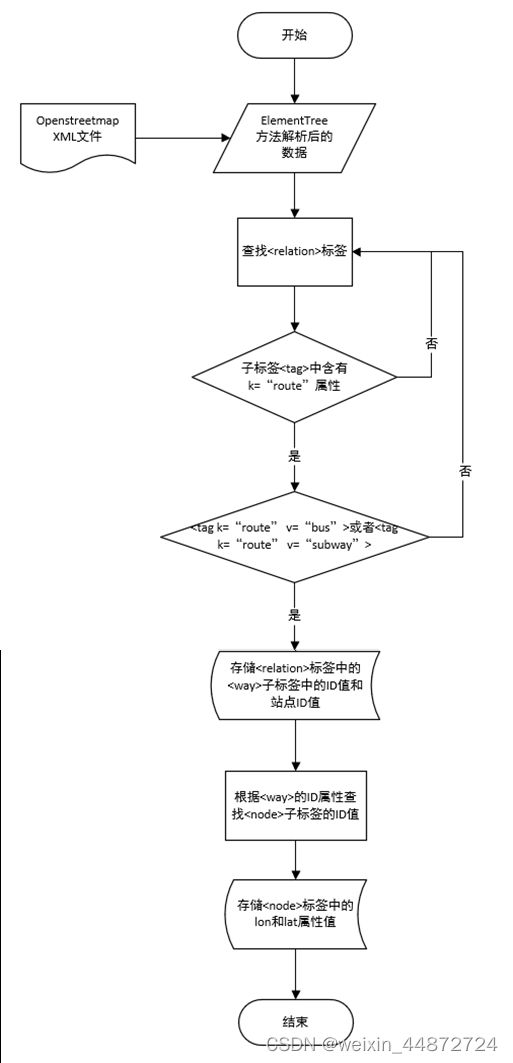
将实际路网信息变成节点和边的数据结构形式并存储。以上海市交通路网为例。首先,通过OpenStreetMap(OSM)提供的Overpass API Query Form获取XML格式的上海市交通路网的信息。
在该XML文件中,可以发现,地理数据的数据结构是带有拓扑性质的数据。地理信息系统的点,线,面以及它们之间的关系通过XML中node,way和relation进行分别描述。各自标签下的tag用于记录其标签的属性信息。
接着,使用ElementTree(元素树)方式对XML文件进行解析。该方式类似一种轻量级的DOM。相对于拥有大量函数的Simple API for XML(SAX)方法和需要将XML数据映射到内存中的树的Document Object Model(DOM)方法。ElementTree可以以更容易被理解的代码形式和更快的速度解析XML。通过ElementTree方法遍历获得搜索所有的
2.不同路网数据获取
OpenStreetMap提供的XML文件中包含了许多不同类型的道路信息,例如公共交通道路,机动车道路,自行车道路或人行道道路等等。
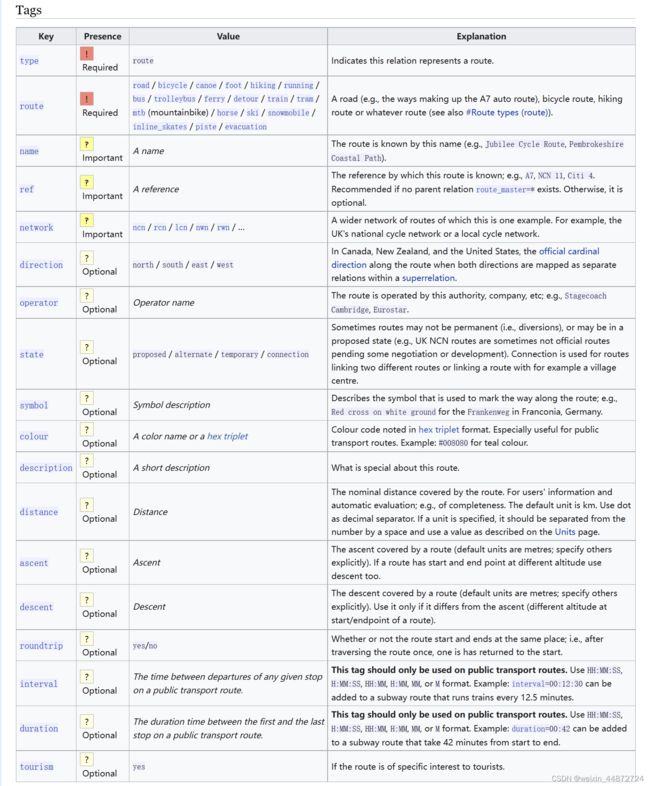
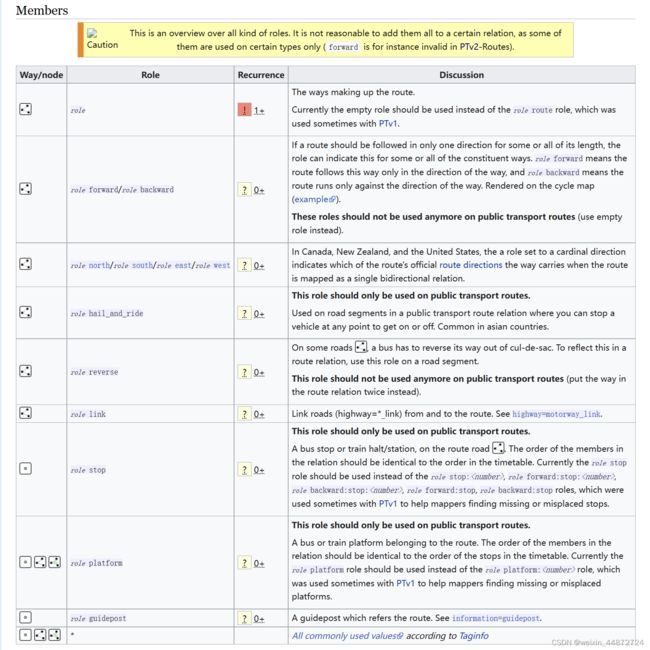
本段将基于OpenStreetMap提供的数据结构解析出公共交通路线数据。公共交通道路信息主要被存储与
图14:
图15: OpenStreetMap官网上
图16: OpenStreetMap官网上
解析公共交通路网数据的步骤如下。首先,需要确定当前标签记录的是道路信息,即
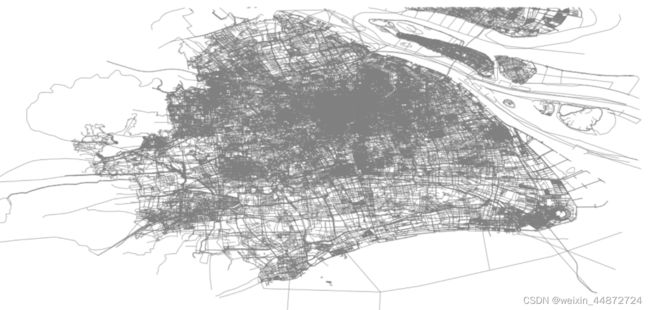
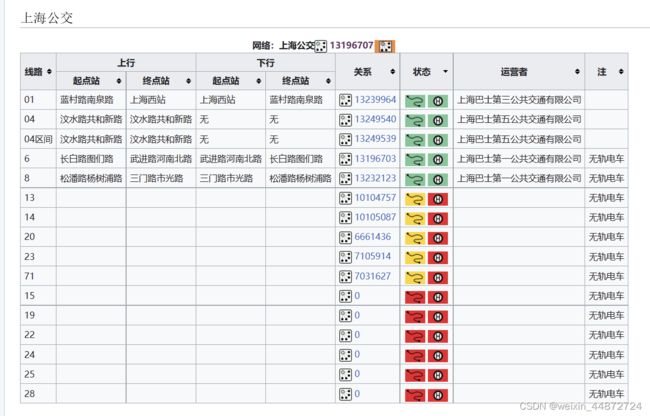
TIP: 由于openstreetmap是一款国外的开源地图数据。因此国内路网数据上会存在一些缺失的现象,导致线路信息不完整。 例如,上海的公共交通线路数据,在openstreetmap中仅有少数线路。下图所示:
3.应用A*算法(A*算法应用于真实上海交通路网)
真实的交通路网地图区别于游戏中的栅格地图不同之处在于,真实的交通路网中的子节点扩展方式是找寻该父节点的最近直系节点,而不是节点的上下左右方位上的四个节点。它们之间的距离也不是固定为1,而是需要通过两节点的经度和纬度进行计算。
在寻找的过程中将使用韩忠民提供的两点的经纬度计算距离的近似公式[16]。假设有A, B两地,它们的纬度和经度分别是(lat1, lon1)和(lat2, lon2)。公式中S表示两地之间的距离(千米),a表示AB两地纬度之差(lat1-lat2),b表示AB两地经度之差(lon1-lon2),6378.137表示地球的半径(千米)。使用该公式计算出的距离精度和谷歌地图的距离精度误差在正负0.2米之内[16]。
然后,遍历地图中所有节点的经度和纬度。将其与起始地和目的地的经度和纬度进行距离计算,找出一定范围内的所有节点,并使用起始列表和目的列表分别保存被找到的节点的ID。接着,将起始列表中的所有节点于目的列表中的所有节点进行组合。两节点组合结果将作为Map对象中的起始节点和目的节点代入A*算法中。Map对象中的节点(node)间的地理距离也将使用韩忠民的距离近似函数进行计算,然后作为Map对象中边(edge)的权重。将节点组合代入A*算法中进行最优路径的寻找,如果不存在路径则会抛出异常。但如果两个节点列表中的所有节点组合的经度和纬度都不能通过A*算法找到它们之间的最优路径,则会扩大附近节点的搜索范围,每次增加10米。直到两个节点列表中出现可以找到最优路径的节点组合,搜索范围不再扩大,程序进入下一步运算。随后,将所有没有抛出异常的节点组合存放在字典中,并找到其中路径方案距离最小的节点组合。输出其节点组合中A*算法返回的字典回溯中的节点ID。将这些节点按照输出顺序进行连接,即可得到两节点之间的最短路径。
结束
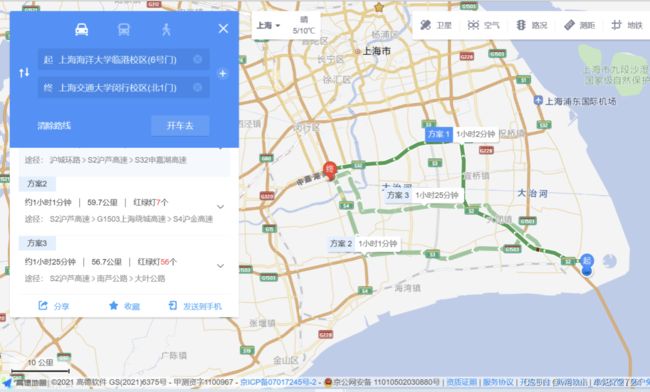
最终测试:(图中显示的是整理过的路径规划数据,但后续还需再整理)
相比较高德地图app:
该项目的缺点:(亲自测试过的)
- openstreetmap的数据不完整性。
- 高德api存在的数据不确定性。
- openstreetmap中的数据还需要进一步整理(当然了,按照上述方式10米10米的增加,可以解决部分路径规划问题。但这并不是真正的解决方案,具体请翻阅【陈舒燕. 基于OpenStreetMap的出行可达性分析与实现[D].上海师范大学,2010.】,上面有数据整理的方法。
- 道路两节点之间取的是直线距离,未考虑道路弯曲的情况。
参考文献:
8. 周小镜. 基于改进A*算法的游戏地图寻径的研究[D].西南大学,2011.
14. 严寒冰,刘迎春.基于GIS的城市道路网最短路径算法探讨[J].计算机学报,2000(02):210-215.
16. 韩忠民.知经纬度计算两点精确距离[J].科技传播,2011(11):196+174.