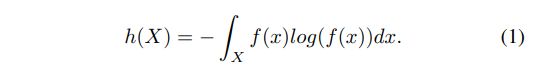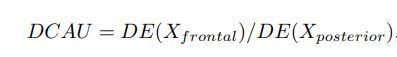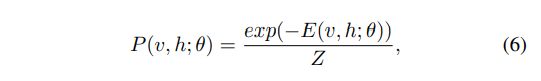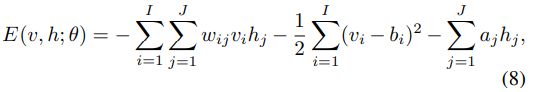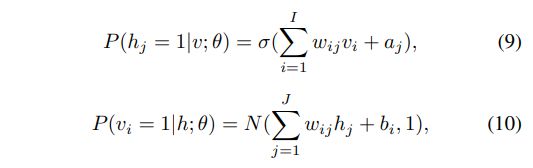EEG-SEED数据集作者的---基线论文阅读和分析

《Investigating Critical Frequency Bands and Channels for EEG-based Emotion Recognition with Deep Neural Networks》

方法：

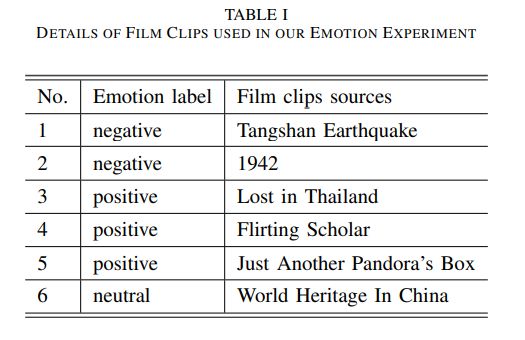
A.预处理根据被试的反应，只选择诱发目标情绪的实验片段进行进一步分析。

将原始脑电图数据降采样至200Hz采样率。目视检查脑电图信号，人工去除受肌电图和脑电图污染严重的记录。在实验中还记录了眼动图，并用于从记录的脑电图数据中识别闪烁伪影。为了滤除噪声和伪影，对EEG数据进行了0.3Hz至50Hz的带通滤波器处理。经过预处理后，我们提取了每部电影时长对应的脑电图片段。EEG数据的每个通道被划分为相同长度的1s周期，互不重叠。一个实验大约有3300个干净的片段。在脑电图数据的每个片段上进一步计算特征。所有信号处理均在Matlab软件中完成。

B.特征提取

一种称为微分熵(DE)[35]的高效特征，[36]扩展了香农熵的思想，用于度量连续随机变量[46]的复杂性。由于EEG数据的低频能量高于高频能量，因此DE具有区分EEG模式低频和高频能量的平衡能力，这是由Duan等人[36]首次引入到基于EEG的情绪识别中。原微分熵的计算公式定义为:

如果随机变量服从高斯分布$N(\mu ,\sigma 2)$，则微分熵可以简单地计算为:

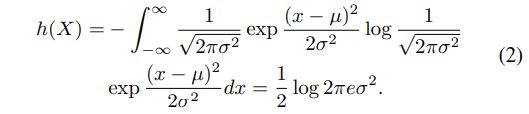
已经证明，对于固定长度的脑电图片段，微分熵等价于某频段[35]的对数能谱。因此，微分熵可以在5个频段(delta: 1- 3Hz, theta: 4-7Hz, alpha: 8-13Hz, beta: 14-30Hz, gamma: 31- 50Hz)中计算，时间复杂度为$O(KNlogN)$，其中K为电极数量，N为样本大小。

针对特定的脑电信号序列，采用256点无重叠汉宁窗口(1s)的短时傅里叶变换提取脑电信号的5个频段。然后计算每个频带的微分熵。由于每个频带信号有62个通道，我们为一个样本提取了310维的微分熵特征。

[38]和[47]的研究表明，不对称的大脑活动(左右侧化和前后尾化)似乎对情绪处理有效。所以我们也计算不对称微分(DASM)和理性的不对称(RASM)特性[36]DE特征之间的差异和比率27双半球不对称电极(F₁,F7, F3, FT7, FC3, T7, P7, C3, TP7 CP3, P3, O1, AF3, F5、F7, F C5, FC1, C5, C1, CP5, CP1, P5, p1, PO7, PO5, PO3, CB1左脑半球,和F p2, F8, F4, FT8, FC4, T8, P8, C4, TP8 CP4, P4, O2, AF4, F6, F8, FC6, FC2, C6, C2, CP6, CP2, P6, p2, PO8, PO6, PO4,右半球CB2)。DASM和RASM分别定义为:

其中$x_{left}$ 和$X_{right}$分别代表左右半球的电极对。我们将DCAU特征定义为23对额后电极(FT7-TP7、FC5-CP5、FC3-CP3、FC1-CP1、FCZ-CP Z、FC2-CP2、FC4-CP4、FC6-CP6、FT8-T P8、F7-P7、F5-P5、F3-P3、F1-P1、F Z-P Z、F2-P2、F4-P4、F6-P6、F8-P8、FP1-O1、F P2-O2、FPZ-OZ、AF3-CB1和AF4-CB2) DE特征之间的差异。DCAU定义为:

其中，Xf rontal和Xposterior表示前后电极对。为了进行比较，我们还提取了常规功率谱密度(PSD)作为基线。PSD、DE、DASM、RASM和DCAU特征的尺寸分别为310、310、135、135和115。我们应用线性动态系统(LDS)方法进一步过滤不相关的成分，并考虑情绪状态的时间动态。

C.深度信念网络分类
深度信念网络是一个具有深度架构的概率生成模型，它使用隐藏变量[25]，[29]来表征输入数据分布。DBN的每一层由一个受限玻尔兹曼机(RBM)组成，RBM包含可见单元和隐藏单元，如图2(a)所示。没有可见-可见的联系，也没有隐藏-隐藏的联系。可见单元和隐藏单元分别有一个偏置向量c和b.

DBN是通过将预定义数量的RBM堆叠在一起来构造的，其中低级RBM的输出是高级RBM的输入，如图2(b)所示。一种高效的贪婪分层算法用于预训练网络的每一层。

在RBM中，联合分布P(v, h;θ)除以可见单位v和隐藏单位h，给定模型参数θ，定义为能量函数E(v, h;θ)

其中Z 是归一化因子：

模型赋给可见向量v的边际概率为：

对于高斯(可见)-伯努利(隐)RBM，能量函数定义为：

其中$w_{ij}$为可见单元$v_i$与隐藏单元$h_j$之间的对称相互作用项，$b_i$和$a_j$为偏置项，$I$和$J$为可见和隐藏单元的个数。条件概率可以有效地计算为：

其中$\sigma (x)=1/(1+exp(x))$， vi取实值，服从均值${\sum }_{j=1}^J{w}_{ij}{h}_j+b_i$，方差为1的高斯分布。

取对数似然对数p(v;θ)，我们可以推导出调整RBM权值的更新规则为

其中$Edata(v_i{h}_j)$是在训练集中观察到的期望，而$Emodel(v_i{h}_j)$是在模型定义的分布下的相同期望。但$Emodel(v_i{h}_j)$难以计算，因此使用梯度的对比散度近似，其中$Emodel(v_i{h}_j)$被运行在数据处初始化的吉布斯采样器取代。有时权重更新中的动量被用于防止陷入局部极小值，正则化可以防止权重变得太大。

在这项工作中，训练分为三个步骤:
1)对每层进行无监督的预训练，
2)对所有层进行无监督的反向传播微调，
3)对所有层进行有监督的反向传播微调。对于无监督微调，展开n个rbm以形成一个2n−1有向编码器和解码器网络，该网络可以通过反向传播[25]，[49]进行微调。图2（c）显示了展开的DBN的图形描述。训练这个深度自编码器的目标是学习每一层之间的权重和偏差，以便重建和输入尽可能接近。对于监督微调，在预训练DBN的顶部添加标签层，并通过误差反向传播更新权重。

实验部分：

A.使用电影片段作为刺激源：

B.被测试人员：

7 males and 8 females; MEAN: 23.27, STD: 2.37，并且进行Eysenck Personality Questionnaire (EPQ)

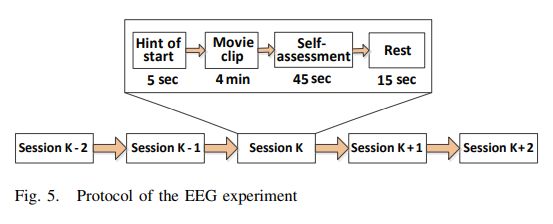
C.测试过程：

实验结论

A.神经模式

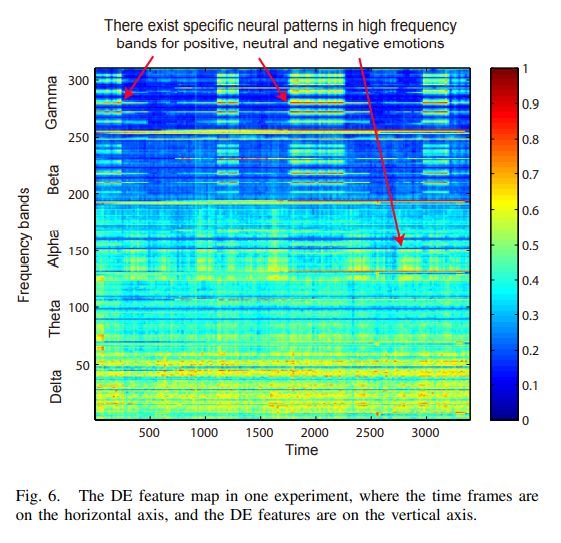
在从五个频段(Delta, Theta, Alpha, Beta和Gamma)提取差分熵特征后，我们进一步研究了与不同情绪相关的神经模式。一个实验的DE特征图如图6所示。通过时频分析，我们发现积极情绪、中性情绪和消极情绪在高频段存在特定的神经模式。对于积极情绪，β和γ频段能量增加，而中性和消极情绪的β和γ频段能量较低。中性情绪和消极情绪的神经模式在β和γ波段有相似的模式，中性情绪有更高能量的α振荡。这些发现为理解情绪在大脑中的加工机制提供了基础证据。

观察到的频率被划分为特定的组，因为特定的频率范围在某些心理状态下更为突出。先前的神经科学研究[54]和[55]已经表明，脑电图的α波段反映了注意力的处理，而β波段反映了大脑中的情绪和认知处理。Li和Lu[22]也表明，EEG的gamma波段适用于以情绪图像为刺激的情绪分类。我们的发现与现有的结果一致。当参与者观看中性刺激时，他们往往更放松，注意力更不集中，这就会引发alpha反应。当处理积极情绪时，beta和gamma反应的能量会增强。

B.分类器训练

在这项研究中，我们系统地比较了K近邻(kNN)、逻辑回归(LR)、支持向量机(SVM)和深度信念网络(DBNs)四种分类器在基于EEG的情绪识别中的分类性能。这些分类器使用上面提到的DE特性作为输入。在情绪实验中，我们收集了15名被试的脑电图数据，每位被试每隔一周左右做两次实验。这里总共评估了30个实验。训练数据和测试数据来自同一实验的不同阶段。训练数据包含9组数据，而测试数据包含6组来自同一实验的数据。

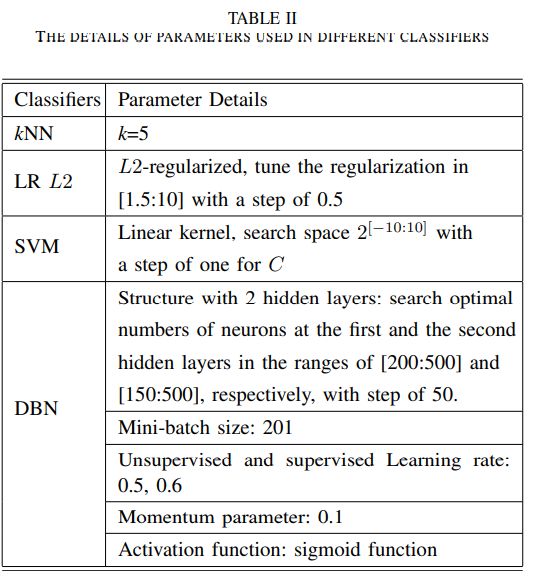
表II显示了不同分类器中使用的参数的详细信息。对于kNN，我们使用k = 5作为基线，与其他分类器进行比较。对于LR，我们采用l2正则化LR，并在[1.5:10]中以0.5的步长调整正则化参数。我们还使用支持向量机对每个脑电图片段的情绪状态进行分类。支持向量机的基本思想是将输入数据通过核传递函数投影到高维特征空间上，这样比在原始特征空间中更容易分离。我们使用LIBSVM软件[56]来实现SVM分类器，并采用线性核。我们搜索参数空间2[−10:10]，对C的步长为1，以找到最优值。

对于深度神经网络，我们构造了一个有两个隐含层的DBN。我们分别在[200:500]和[150:500]范围内搜索第一和第二隐藏层中步长为50的最优神经元数量。在实验中，我们将无监督学习率和监督学习率分别设置为0.5和0.6。我们还在权重更新中使用动量来防止陷入局部极小值。在将DE特征放入DBN之前，这些特征的值通过减去平均值，除以标准差，最后加上0.5，在0到1之间缩放。本文采用DBNToolbox Matlab代码[44]实现DBN。

C.分类表现

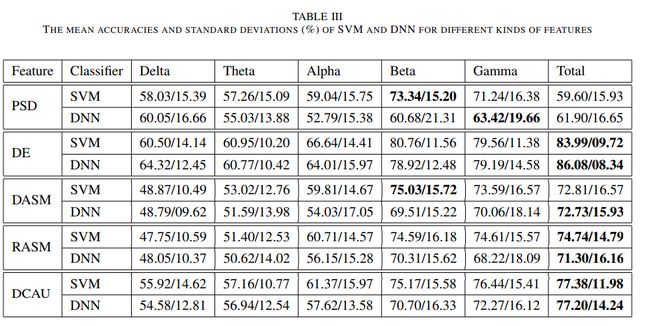
1、研究不同特征类型和两种算法的分类性能

结论：DE特征+DNN+Total频带得到最优结果，同时说明Beta和Gamma这两个频带的分类结果较优。

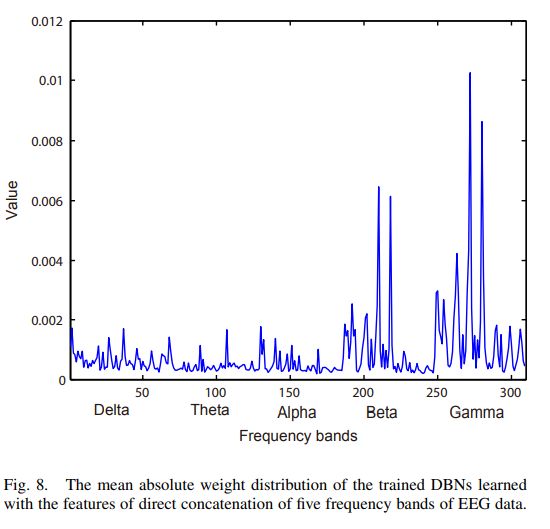
不同频带的权重：

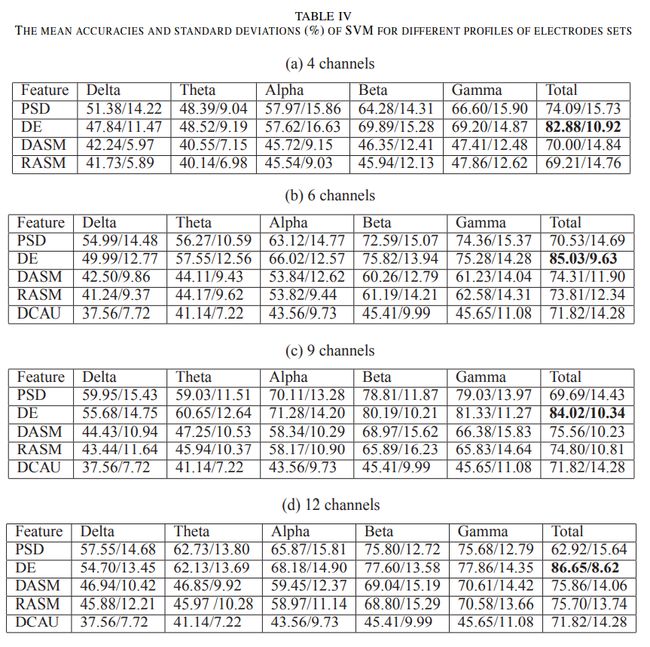
2、研究不同通道数的分类性能

结论：使用12个通道+DE得到最优结果。甚至比全通道的结果要优。

所选择的通道示意图：