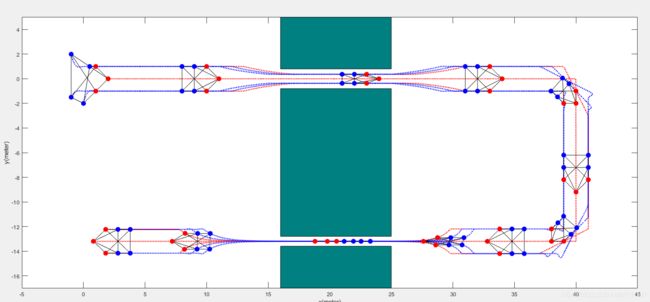
论文记录:Affine Formation Maneuver Control of Multiagent Systems
注意:本仿真图只是起到了演示效果,中间过程速度产生突变,实际中是不允许的。需要进行速度规划,这一点论文中仿真图更为贴合实际,论文仿真就做了速度规划。
参考论文:Zhao, S. (2018). Affine Formation Maneuver Control of Multiagent Systems. IEEE Transactions on Automatic Control, 63(12), 4140–4155.
突然发现有个博主写得很好,参考:用MATLAB仿真仿射队形变换(affine formation maneuver)
%论文:2018 Affine Formation Maneuver Control of Multiagent Systems
%!!!注意只是仿真演示在实际情况下仿真不符合实际的情况,例如速度进行跳变,瞬间变化。现实中不存在这样的情况。要做对应的速度规划才能用!
%程序功能: 1.实现编队; 2.编队平移/旋转/尺寸缩放/shear(剪切变换)/以及这些变换的组合
% 二阶积分器,两种情况:1.leader的速度是常数;2.leader的速度是时变的
%问题;1.算法中间的积分是叠加的,不是真正意义上的积分;
%二维平面
% 有些图形没画啊,根据需要自己添加。
%author: wuhongjun
%date : 2021.5.30
close all
clc;
clear;
%% 输入初始化参数
AgentsNum = 7; %智能体的数量
Leaders = 3;
Followers = 4;
Dim = 2; % 维度
% noiminal formation:P(r),后面不会用到,在此只是说明标准编队的形状
P_r = [2 0;
1 1;
1 -1;
0 1;
0 -1;
-1 1;
-1 -1];
X0 = [2, 0, 1, 1, 1, -1, 0.5, 1, 0, -2, -1, 2, -1, -1.5]'; % 后面是需要改变的
Ut = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]'; %初始控制输入,二阶就对应加速度
Vt = [0.2, 0, 0.2, 0, 0.2, 0, 0, 0, 0, 0, 0, 0, 0, 0]'; %初始控制输入,二阶就对应加速度
%计算 stress matrix,论文中用Ω(欧米伽)表示,仿真中用L=D-A表示
%A 对应的邻接矩阵
A = [ 0 0.2741 0.2741 -0.137 -0.137 0 0 ;
0.2741 0 0 0.5482 0 0 -0.137 ;
0.2741 0 0 0 0.5482 -0.137 0 ;
-0.137 0.5482 0 0 0.0685 0.2741 0 ;
-0.137 0 0.5482 0.0685 0 0 0.2741;
0 0 -0.137 0.2741 0 0 0.137 ;
0 -0.137 0 0 0.2741 0.137 0 ;];
D = zeros(AgentsNum,AgentsNum);
% 拉普拉斯矩阵
for i = 1:AgentsNum
add = 0; % 累加时使用的变量
% g_ij = zeros(Dim,1);
for j = 1:AgentsNum
add = add + A(i,j);
end
D(i,i) = add;
end
% H = D
% J = P
L = D - A
M = L (4:7,4:7)
k = rank(M)
I = eye(2)
L_ = kron(L,I)
L_ff = L_(Dim*Leaders+1:Dim*AgentsNum,Dim*Leaders+1:Dim*AgentsNum);
L_fl = L_(Dim*Leaders+1:Dim*AgentsNum,1:Dim*Leaders);
final = -inv(L_ff)*L_fl*X0(1:Dim*Leaders,1);
%初始化增益Kp,Ki
Kp = 2;
Kv = 2;
Ki = 1;
% leaderfollowers
tBegin = 0; % 开始时间
tEnd = 420; % 结束时间
delta_t= 0.01; % 最小时间间隔
times = (tEnd-tBegin) / delta_t; % 迭代计算次数
X(:,1) = X0;
% X的第一列等于X0,初始化坐标
V(:,1) = Vt;
U(:,1) = Ut; % 初始时刻的控制输入
t(1) = tBegin; % 时间间隔记录表
i = 1;
% Xr = zeros(24,1); % 每一次的目标值
Vc = [0.2, 0 ]'; % 二维的
Alpha = [0, 0, 0]';% 注意看论文实际是需要考虑alphai_i和alphai_j的关系,公式(8)
v_change = 0.03;
%% 单独的scale测试,水平/垂直/整体尺寸
while(i <= times)
Xt = X(:,i); % X(:,i)表示第i列保存每次迭代的数据信息, 上一时刻的位置
V_last = Vt; % 上一时刻的速度
C_Xr = zeros(2,1); % 标
for j =1:Leaders % 这里只考虑leaders之间的质心,如果考虑完整的话,应该算出整个编队的质心
C_Xr = C_Xr+Xt(Dim*(j-1)+1:Dim*j,1); % 质心坐标
end
C_Xr = 1 / Leaders * C_Xr;
% 单独的scale测试
for m =Leaders+1:AgentsNum % followers的速度
add = zeros(Dim,1);
for n = 1:AgentsNum
add = add + A(m,n) *(Kp * (Xt(Dim*(m-1)+1:Dim*m,1) - Xt(Dim*(n-1)+1:Dim*n,1)) + Kv *(Vt(Dim*(m-1)+1:Dim*m,1) - Vt(Dim*(n-1)+1:Dim*n,1)) - Ut(Dim*(n-1)+1:Dim*n,1));
end
Ut(Dim*(m-1)+1:Dim*m,1) =-1/D(m,m) * add;
end
Vt = Vt + delta_t * Ut;
% Kp,Kv 大于0
Xt1 = Xt + delta_t * Vt; % x = x + h*u 相当于进行积分,计算每次更新后的信息
X(:,i+1) = Xt1; % 添加更新后的Xt值,存储更新后的信息
V(:,i+1) = Vt;
U(:,i+1) = Ut; % 添加更新后的Ut值,保存每次的控制信息
t(i+1) = tBegin + i * delta_t; % 添加更新后的t值,计算时间值
i = i+1;
%下面的方法是通过alpha改变leader的速度,改变尺寸,时间控制类型一。用于单独测试scale变换
time1 = 60; % 开始缩小
time2 = 80; % 开始平移
time3 = 130; % 开始放大
time4 = 150; % 开始平移
time5 = 190; % 开始旋转
time6 = 194; % 开始向下平移
time7 = 240; % 开始旋转
time8 = 244; % 开始平移
time9 = 280; % 开始shear切变
time10 = 310; % 开始平移
time11 = 360; % 开始shear切变
time12 = 390; % 开始平移
if i > 100*time1 && i <100*time2
for j =1:Leaders % leader的速度
Vt(Dim*j,1) = Vc(Dim,1) -0.05*(Xt(Dim*j,1)-C_Xr(Dim, 1)); % 垂直尺寸变化
end
elseif i > 100*time2 && i <100*time3
for j =1:Leaders % leader的速度
Vt(Dim*j,1) = Vc(Dim,1) ; % 垂直尺寸变化
end
elseif i>100*time3 && i< 100*time4
for j =1:Leaders % leader的速度
Vt(Dim*j,1) = Vc(Dim,1)+0.05*(Xt(Dim*j,1)-C_Xr(Dim, 1)); % 垂直尺寸变化
end
elseif i> 100*time4 && i< 100*time5
for j =1:Leaders % leader的速度
Vt(Dim*j,1) = Vc(Dim,1) ; % 垂直尺寸变化
end
elseif i >100*time5 && i < 100*time6
Vt(1:6,1) = [0, -1, 0.5, -1, 0, -0.5]'; %初始控制输入,二阶就对应加速度
elseif i > 100*time6 && i < 100*time7
Vt(1:6,1) = [0, -0.2, 0, -0.2, 0, -0.2]'; %初始控制输入,二阶就对应加速度
elseif i > 100*time7 && i < 100*time8
Vt(1:6,1) = [-1, 0, -1, -0.5, -0.5, 0]'; %初始控制输入,二阶就对应加速度
elseif i > 100*time8 && i < 100*time9
Vt(1:6,1) = [-0.2, 0, -0.2, 0, -0.2, 0]'; %初始控制输入,二阶就对应加速度
elseif i > 100*time9 && i < 100*time10
% 在1/5 时间处变换队形,但是问题又来了,在实际中怎么知道队形是变换到什么尺度合适,因为只要Alpha不为0,他就始终变换队形(放大或者缩小)。
% 怎么把握这个度
for j =1:Leaders % leader的速度
Vt(Dim*j,1) = -Vc(Dim,1) -0.2*(Xt(Dim*j,1)-C_Xr(Dim, 1)); % 垂直尺寸变化
end
if Xt(Dim*3, 1) ~= C_Xr(Dim,1) % 现实情况下应该考虑y相差不大就让X方向的尺寸保持一致,而不是让y完全一致
Vt(Dim*3-1,1) = -Vc(Dim-1, 1) +0.025;
elseif Xt(Dim*3, 1) == C_Xr(Dim,1)
Vt(Dim*3-1,1) = -Vc(Dim-1, 1);
end
elseif i > 100*time10 && i< 100*time11
for j =1:Leaders % leader的速度
Vt(Dim*j,1) = -Vc(Dim,1); % 垂直尺寸变化
end
Vt(Dim*3-1,1) = -Vc(Dim-1, 1);
elseif i>100*time11 && i< 100*time12
for j =1:Leaders % leader的速度
Vt(Dim*j,1) = -Vc(Dim,1) +0.2*(Xt(Dim*j,1)-C_Xr(Dim, 1)); % 垂直尺寸变化
end
Vt(Dim*3-1,1) = -Vc(Dim-1, 1) -0.025;
elseif i> 100*time12
for j =1:Leaders % leader的速度
Vt(Dim*j,1) = -Vc(Dim,1); % 垂直尺寸变化
end
Vt(Dim*3-1,1) = -Vc(Dim-1, 1);
end
end
Draw_Num = [1 4500 11000 16000 19200 22000 24200 26000 28600 33000 38800 42000]; % shear
%%结果显示
%绘制图像
figure(1);
subplot(3,1,1)
plot(t,X(1,:), t,X(3,:), t,X(5,:), t,X(7,:), t,X(9,:), t,X(11,:),t,X(13,:), 'linewidth',2.0)
legend("x_1","x_2","x_3","x_4","x_5","x_6","x_7");
xlabel('Times/收敛次数');
ylabel('States/状态值');
subplot(3,1,2)
plot(t,U(1,:), t,U(3,:), t,U(5,:), t,U(7,:), t,U(9,:), t,U(11,:), t,U(13,:),'linewidth',2.0)
legend("u_1","u_2","u_3","u_4","u_5","u_6","u_7");
xlabel('Times/收敛次数');
ylabel('加速度');
subplot(3,1,3)
plot(t,V(1,:), t,V(3,:), t,V(5,:), t,V(7,:), t,V(9,:), t,V(11,:),t,V(13,:), 'linewidth',2.0)
legend("V_1","V_2","V_3","V_4","V_5","V_6","V_7");
xlabel('Times/收敛次数');
ylabel('速度');
figure(3);
for i = 1:Leaders
plot(X(i*Dim-1,:),X(i*Dim,:), ':r','linewidth',2); % -实线 -- 虚线 :点线 -.点划线
hold on
end
for i = Leaders+1:AgentsNum
plot(X(i*Dim-1,:),X(i*Dim,:), ':b','linewidth',2); % -实线 -- 虚线 :点线 -.点划线
hold on
end
axis equal % 绘制数据,并使用 axis equal 命令沿每个轴等间距隔开刻度单位
axis([-5 45 -17 5]) % axis([Xmin Xmax Ymin Ymax])
xlabel('x(meter)');
ylabel('y(meter)');
NumOfPlot = size(Draw_Num, 2); %[m,n] = size(a) m=size(a,1)行 n = size(a,2)列
for m = 1:NumOfPlot
Num = Draw_Num(m);
x = [X(1,Num),X(3,Num); X(1,Num),X(5,Num); X(1,Num),X(7,Num); X(1,Num),X(9,Num); X(3,Num),X(7,Num); X(3,Num),X(13,Num); X(5,Num),X(11,Num); X(5,Num),X(9,Num); X(7,Num),X(9,Num); X(7,Num),X(11,Num); X(9,Num),X(13,Num); X(11,Num),X(13,Num);]'; % 记得转置
y = [X(2,Num),X(4,Num); X(2,Num),X(6,Num); X(2,Num),X(8,Num); X(2,Num),X(10,Num); X(4,Num),X(8,Num); X(4,Num),X(14,Num); X(6,Num),X(12,Num); X(6,Num),X(10,Num); X(8,Num),X(10,Num); X(8,Num),X(12,Num); X(10,Num),X(14,Num); X(12,Num),X(14,Num); ]';
hold on
plot(x,y,'-ko','MarkerSize',8,'MarkerEdgeColor','blue','MarkerFaceColor',[0 0 1]);
x = [X(1,Num),X(3,Num);X(1,Num),X(5,Num);]'; % 记得转置
y = [X(2,Num),X(4,Num);X(2,Num),X(6,Num);]';
% z = [X(3,Num),X(6,Num);]';
hold on
plot(x,y,'o','MarkerSize',8,'MarkerEdgeColor','red','MarkerFaceColor',[1 0 0]);
end
rectangle('Position',[16 0.8 9 4.2],'FaceColor',[0 .5 .5])
rectangle('Position',[16 -12.8 9 12],'FaceColor',[0 .5 .5])
rectangle('Position',[16 -17 9 3.4],'FaceColor',[0 .5 .5])