现代机器人读书笔记 Chapter2：Configuration Space

Chapter2：Configuration Space

本章将所有机器人都建模为刚体的连杆。

2.1 自由度计算

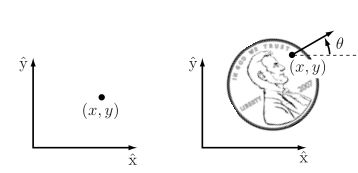
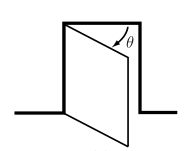
对于机器人来说，首先要关注的是它在哪里？如何描述机器人的位置，很简单，即对机器人上的每个点做出位置描述，由于机器人的连杆是刚性且形状已知，那么仅需几个坐标就可以描述，如图，门的位置就可以用铰链的角度θ来描述。

图1 门

平面上某一点的位置可以用两个坐标(x, y)来描述,硬币正面朝上放在平板上的位置可以用三个坐标来描述:两个坐标(x, y)表示硬币上某一点的位置,角度θ表示硬币的朝向。这些坐标都在连续的实数域内取值。

图2 坐标描述

由此，我们引出自由度的定义，机器人的自由度(dof)是表示其位形所需的最小实值坐标数。

上述我们的描述中，门就有一个自由度，而硬币则有三个自由度，这里需要注意，虽然硬币有正反面两种状态，但是正反面是一个离散集合，并非连续的实数空间。

这样本章的第一个定义就出现了，加粗部分是C空间的定义：

Definition 1： The configuration of a robot is a complete specification of the position of every point of the robot. The minimum number n of real-valued coordinates needed to represent the configuration is the number of degrees of freedom (dof) of the robot.

The n-dimensional space containing all possible configurations of the robot is called the configuration space (C-space). The configuration of a robot is represented by a point in its C-space.

接下来我们探究刚体的自由度:

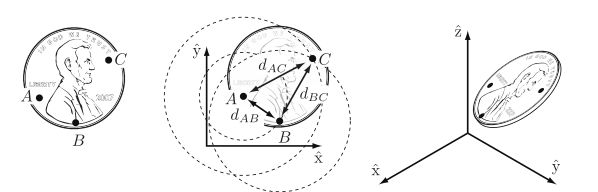
以放在桌面上的硬币为例，在其上选择三个点A、B、C，建立直角坐标系o-xy，如果这些点可以独立放置在平面上的任何位置，硬币将有6个自由度——3个点每个有2个自由度。但是，A、B、C三点的距离是一个定值，记其坐标为:$\left(x_A,y_A\right),\left(x_B,y_B\right),\left(x_c,y_c\right)$.

他们满足以下关系：
$$\begin{array}{l}d(A,B)=\sqrt{{\left(x_A-x_B\right)}^2+{\left(y_A-y_B\right)}^2}=d_{AB},\\ d(B,C)=\sqrt{{\left(x_B-x_C\right)}^2+{\left(y_B-y_C\right)}^2}=d_{BC},\\ d(A,C)=\sqrt{{\left(x_A-x_C\right)}^2+{\left(y_A-y_C\right)}^2}=d_{AC}.\end{array}$$
要确定硬币的自由度数，首先选择A点的坐标 ，这样由于约束条件，B点就只能在以A点为圆心的圆上，此时B相对于A位置的确定仅仅只需要B相对于A的夹角θ即可，一旦A和B的坐标都确定，那这样C点的位置就有两种情况，在以A点为圆心的圆以及和B点为圆心的圆的交点处，这恰好对应着硬币为正反面的两个位置，由此，硬币在平面上有三个自由度，即$(x,y,\theta )$。

如果我们在硬币上再选择一点D，重复上述的计算过程，可以很容易得出引入的D点坐标将被消掉，因此没必要再去考虑别的点。

图3 自由度计算说明图

那么对于确定刚体系统的自由度数，有没有什么通用的计算方法呢，常用的规则如下：
$$degreesoffreedom=(sumoffreedomsofthepoints)-(numberofindependentconstraints)$$
这个规则也可以用描述系统的变量和独立方程的数量来表示:
$$degreesoffreedom=(numberofvariables)-(numberofindependentequations)$$
很明显硬币的例子就可以用系统的变量数目6减去独立方程的数目3得到，在平面上放置的硬币的自由度为3.

上述规则还可以推广用于确定三维空间中刚体的自由度，依旧以硬币为例，假设其在空间内任意位置，那这样依旧使用规则进行计算，系统的独立变量数目为9减去独立方程的数目3，那么在空间中的硬币的自由度为6.

通过上述例子，在三维空间中的刚体，称为spatial rigid body，有6个自由度，在二维平面中的刚体，称为planar rigid body，有3个自由度，在二维平面中的刚体可以看成是空间6自由度的刚体附加了$z_a=z_b=z_c=0$ ,也可以是其余两个参数)的约束。

由上述的两个规则，就可以得到确定一般机器人自由度的规则：
$$degreesoffreedom=(sumoffreedomsofthebodies)-(numberofindependentconstraints)$$
了解了刚体系统自由度的计算，下面我们进入机器人自由度的计算：

再次考虑一开始提到的的门的例子，门由一个单一刚体通过铰链连接到墙壁。很容易看出门只有一个自由度，用铰链接的角度来表示。如果没有铰链，门就可以在三维空间中自由移动，有6个自由度，通过铰链将门与墙连接，门的运动受到五个独立约束，只能转动，也可以这样理解或者，门可以从上面看，视为一个平面体，有三个自由度。然后铰链关节施加两个独立的约束，只有一个独立的坐标。

上述的描述我们可以看出，铰链的存在使得自由度降低了，对于主要由关节和连杆组成的机器人来说，能否通过计算关节和连杆数目确定机器人的自由度呢，答案是肯定的，这就是用于计算机器人自由度的$\text { Grübler’s formula} $.

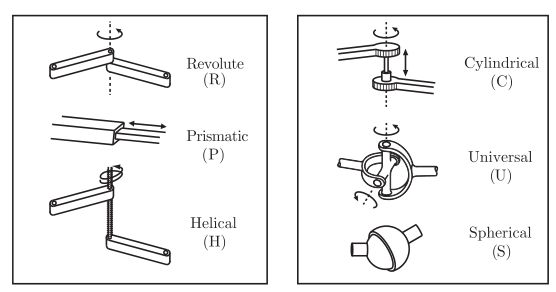
在进入公式之前，我们需要了解机器人中都有哪些关节：

图4 常见关节

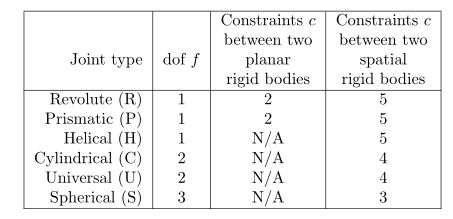
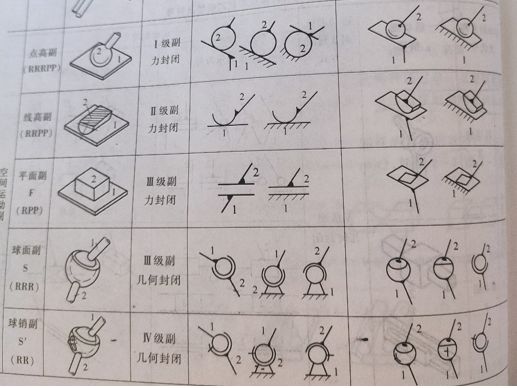
各关节的自由度数和约束数目如下表所示：

有了这些，我们就可以开始介绍来计算机器人的自由度，废话不多说，上公式：

注意：本公式只有在所有关节约束都是独立的情况下才成立。如果它们不是独立的，那么公式就提供了自由度数目的下界。

说实话，看这英文是否大家都很懵圈，因此推荐大家去看孙恒，陈作模，葛文杰.机械原理（第八版）[M].高等教育出版社，2013:195-260，第2章第5节：机构自由度的计算，空间机构自由度计算公式为：
$$F=6n-\sum _{i=1}^5{\mathrm{i}\mathrm{p}}_{\mathrm{i}}$$
式中n为活动构件数，即机构的构件数N减去机架，$N=n-1$,$p_i$为$i$级副的个数,$i$为$i$级副的约束数目，看下面几张图：

图5 空间运动副图

图6 空间运动副图

是不是和英文文献的表很相似，这样中英文的公式就对上了，下面用一个例子来展示如何计算：

图7 仿人机械臂

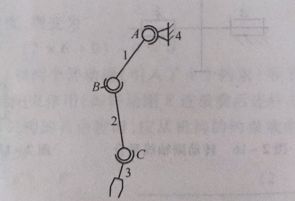
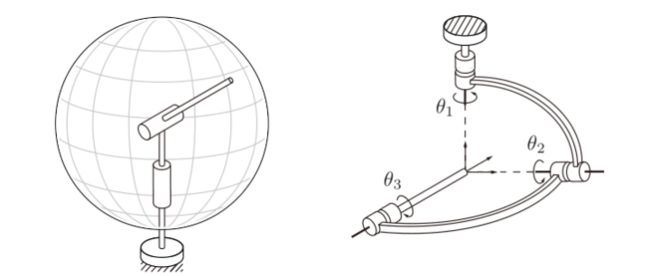
这是一个仿人机械臂，那由人的身体结构可以得到，肩关节和腕关节为球面副，肘关节为球销副，以人体肩部为机架，那么我们使用公式来进行计算：

活动构件数n为4-1=3，球面副按照图可知是三级副，球销副是四级副，那么就有两个三级副，1个四级副，几级副就意味着有几个约束，那么四级副有4个约束，自由度,6-4=2,同理三级副就是3，这样代入公式可得，仿人机械臂的自由度为：6x3-2x1-3x2=8

自由度为8>6表示仿人机械手运动的灵活度较高，有很好的绕障工作能力。

通过上述例题，空间自由度的计算是否就很简单了呢，只需要知道活动构件数，几级副的数目再结合几何结构就可以很方便算出。

2.2 拓扑学

拓扑学部分，这里着实抽象，高能预警：

接下来探讨C空间的拓扑结构和表示，之前的讨论，一直在关注机器人自由度数。然而，C空间的形状拓扑结构也很重要。

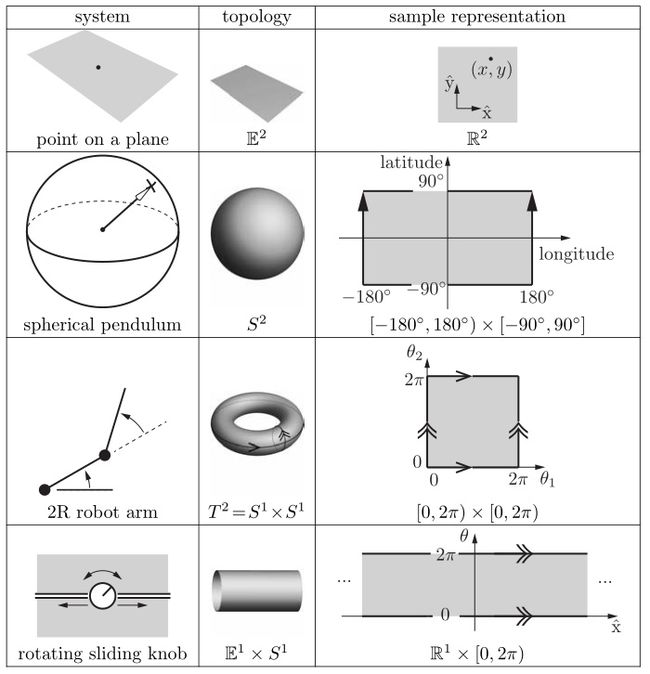
考虑一个在球面上移动的点。点的C空间是二维的，因为点的位置可以用纬度和经度两个坐标来描述。对于在平面上移动的点，也有一个二维的C空间，即坐标(x, y)。显而易见，虽然一个平面和一个球体的表面都是二维的，但平面无限延伸，而球体环绕包裹。

与平面不同的是，一个较大的球体与原来的球体有着相同的形状，因为它们以相同的方式环绕，仅仅只是直径不同。椭圆形的橄榄球也类似于球形，橄榄球和球体之间的区别是橄榄球是球体向一个方向拉伸产生的。

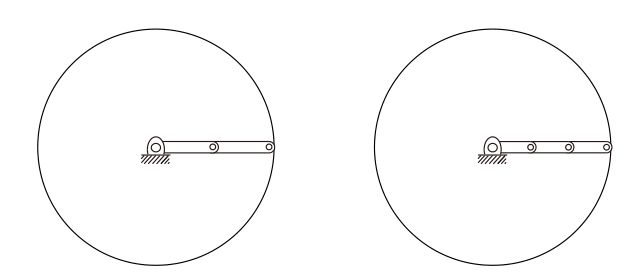
实线的开区间(a, b)可以变形为开半圆，通过下图所示的做法，这个开放的半圆也可以变形为真实的直线即从半圆中心的一点开始，画一条与半圆相交的射线，然后在半圆上方画一条线，这些射线表明，半圆上的每一点都可以拉伸到直线上的一点，反之亦然。因此，开区间可以连续变形为直线，开区间和直线在拓扑上是等价的。

图8 开区间的拓扑表示

小球体、大球体和足球的二维表面都有相同的形状，但其余平面的形状是不同的，这种想法是通过表面的拓扑来表达的。在这本书中，不进行严格的处理，如果一个空间可以在不切割或粘合的情况下不断变形成另一个空间，那么这两个空间在拓扑上是等价的。球体可以简单地通过拉伸变形成橄榄球，而不需要切割或粘合，因此这两个空间在拓扑上是等价的。但是，你不能在不切割球体的情况下把它变成平面，所以球面和面在拓扑上是不相等的。

拓扑上不同的一维空间包括圆、直线和直线的闭合区间。圆被数学的描述为$S$或$S^1$,即一维球面，线被写作$E$或$E^1$，表示一维的欧几里德(或"平坦")空间，因为$E^1$中的点通常用实数表示(在选择原点和长度尺度之后)，所以它通常写成$R$或$R^1$，包含其端点的直线的闭区间可以写成[a,b]包含于 $R^1$ ，开区间(a, b)不包括端点a和b，拓扑上等同于一条线，因为开区间可以拉伸成一条线，如图所示。

闭区间在拓扑上不等同于直线，因为直线不包含端点。

在高维中， $R^n$ 是n维欧几里德空间，$S^n$ 是(n + 1)维空间中球面的n维曲面，例如，$S^2$ 是三维空间中球体的二维表面。

注意，空间的拓扑是空间本身的一个基本属性，它与我们如何选择坐标来表示空间中的点无关。例如，要表示圆上的一点，我们可以引用这个点通过从圆心到点的角度θ。或者，我们可以选择一个以圆心为原点的参考系，用这两个坐标来表示这个点（x，y）通过表达式$x^2+y^2=1$ ，无论我们选择什么坐标，空间本身都不会改变。

有些C空间可以表示为两个或多个低维空间的笛卡尔积（笛卡尔乘积是指在数学中，两个集合X和Y的笛卡尔积（Cartesian product），又称直积，表示为$X\times Y$，第一个对象是X的成员而第二个对象是Y的所有可能有序对的其中一个成员）也就是说，C空间中的点可以表示为低维空间中点表示的并集。这里举例省略了，对拓扑学感兴趣的话可以去看看。

为了便于计算，必须有一组由实数组成的数字表示，这时向量是非常有力的数学工具。但需要注意的是，同样的一个点在三维空间中可以有不同的坐标，这取决于原点和坐标系的选择，但是底层空间的拓扑结构都是一样的。

图9 典型的拓扑空间表示

虽然选择一个参考坐标系和长度比例尺并使用一个向量来代表欧几里得空间中的点是很自然的，但是代表一个弯曲空间上的点，比如一个球体，就不那么明显了。

球体上点坐标的一种解决方案是使用经度和纬度。选择n个坐标或参数来表示n维空间称为空间的显式参数化。这样的显式参数化对于特定范围的参数是有效的，但是如果你在南北极附近行走，那么球体的经纬度表示就让人头疼，迈出一小步就会导致坐标的巨大变化，因此北极和南极是表示法的奇点，而奇点的存在就是球面与平面不相同的拓扑带来的结果。选择经度和纬度描述球面空间，这些奇点的位置与球本身无关，球的底层拓扑结构在哪里是一样的，这一切都与所选择的表示方式有关。

当将速度表示为坐标的导数时，奇点带来了问题，因为在奇点附近速度值可能趋于无穷，即使球上的点以恒定的速度移动，如果用(x, y, z)表示这个点，速度为$\sqrt{{\dot{x}}^2+{\dot{y}}^2+{\dot{z}}^2}$ ，如果奇点无法达到，那么可以忽略这个问题。如果可以达到，有两种方法可以克服这个问题。

（1）在空间上使用多个坐标图，其中每个坐标图都是只覆盖空间的一部分的显式参数化，这样在每个图中就没有奇点。

（2）使用隐式表示，而不是显式参数化。隐式表示法将n维空间视为嵌入在超过n维的欧几里德空间中，就像一个二维单位球可以被视为嵌入在三维欧几里德空间中的表面一样。在之后的各个章节中将使用隐式表示。

对于包含一个或多个闭环的机器人，通常隐式表示比显式参数化更容易获得。例如，如图所示的平面四杆机构，它有一个自由度。这四个连杆总是形成一个闭环的事实可以用以下三个方程表示:
$$\begin{array}{rlr}& L_1\cos {\theta }_1+L_2\cos \left({\theta }_1+{\theta }_2\right)+\cdots +L_4\cos \left({\theta }_1+\cdots +{\theta }_4\right)& =0\\ & L_1\sin {\theta }_1+L_2\sin \left({\theta }_1+{\theta }_2\right)+\cdots +L_4\sin \left({\theta }_1+\cdots +{\theta }_4\right)& =0\\ & {\theta }_1+{\theta }_2+{\theta }_3+{\theta }_4-2\pi & =0\end{array}$$

图10 平面四杆机构（闭环）

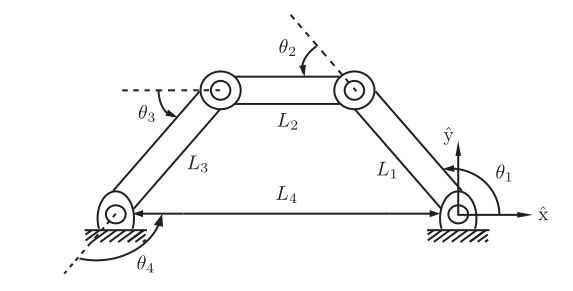
上述方程被称为loop-closure equations。对于四杆机构，它们由一组四个未知数的三个方程给出。所有解的集合在四维关节空间中形成一维曲线，构成了C空间。

因此，对于包含一个或多个闭环的一般机器人，C空间可以隐式地用列向量表示：
$$\theta ={\left[\begin{array}{lll}{\theta }_1& \cdots & {\theta }_n\end{array}\right]}^{\mathrm{T}}\in {\mathbb{R}}^n$$
和这种形式的k（k<=n）个独立方程的loop-closure equations,这种约束被称为完整约束，它能降低C空间的维数,C空间可以看作是一个维数为n-k的曲面（假设所有约束都是独立的包含进$\mathbb{R}^{n} $）：
$$g(\theta )=\left[\begin{array}{c}{g}_1\left({\theta }_1,\dots ,{\theta }_n\right)\\ ⋮\\ g_k\left({\theta }_1,\dots ,{\theta }_n\right)\end{array}\right]=0$$
假设闭链机器人的loop-closure equations为$g(\theta)=0 $，$g: \mathbb{R}^{n} \rightarrow \mathbb{R}^{k}$，以运$\theta\left( t \right)$动，也满足 $g(\theta (t))=0$，就有：
$$\frac{d}{dt}g(\theta (t))=0$$
即：
$$\left[\begin{array}{c}\frac{\partial g_1}{\partial {\theta }_1}(\theta ){\dot{\theta }}_1+\cdots +\frac{\partial g_1}{\partial {\theta }_n}(\theta ){\dot{\theta }}_n\\ ⋮\\ \frac{\partial g_k}{\partial {\theta }_1}(\theta ){\dot{\theta }}_1+\cdots +\frac{\partial g_k}{\partial {\theta }_n}(\theta ){\dot{\theta }}_n\end{array}\right]=0$$
还可表示为：
$$\left[\begin{array}{ccc}\frac{\partial g_1}{\partial {\theta }_1}(\theta )& \cdots & \frac{\partial g_1}{\partial {\theta }_n}(\theta )\\ ⋮& \ddots & ⋮\\ \frac{\partial g_k}{\partial {\theta }_1}(\theta )& \cdots & \frac{\partial g_k}{\partial {\theta }_n}(\theta )\end{array}\right]\left[\begin{array}{c}{\dot{\theta }}_1\\ ⋮\\ {\dot{\theta }}_n\end{array}\right]=0$$
写作：
$$\frac{\partial g}{\partial \theta }(\theta )\dot{\theta }=0,\begin{array}{rl}\dot{{\theta }_i}\text{ 表示 }{\theta }_i\text{ 对时间t的一阶导数}& ,\partial g(\theta )/\partial \theta \in {\mathbb{R}}^{k\times n}，\theta ,\dot{\theta }\in {\mathbb{R}}^n\end{array}$$
继续化简，有：
$$\begin{gathered} A(\theta )\dot{\theta }=0 \\ \frac{\partial g}{\partial \theta }(\theta )=A\left(\theta \right) \end{gathered}$$
这种形式的速度约束称为Pfaffian-constraints,可以把$g\left(\theta \right)$ 看作的$A\left(\theta \right)$积分， 因此$g\left(\theta \right)=0$的完全约束也被称为可积约束（integrable constraints)，即它们所提供的速度约束可以积分得到等效的结构约束。

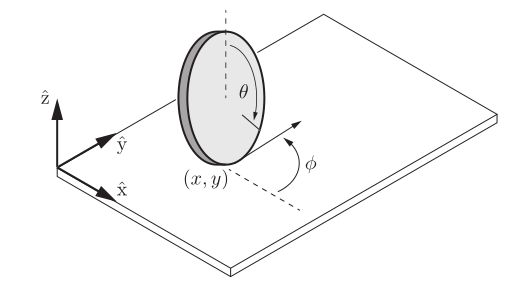
再来考虑另一类与完全约束完全不同的Pfaffian-constraints， 用一个具体的例子来说明，考虑一枚半径为r的硬币在如图所示的平面上滚动：

图11 硬币在平面上滚动

硬币的外形由平面上的接触点(x, y)给出，转向角为$\varphi$，旋转角为$\theta$ ，描述硬币的C空间就是 $\mathbb{R}^{2} \times T^{2} $,$T^{2}$ 是转向角$\varphi$,旋转角$\theta$形成的二维环，整个C空间是四维的。

硬币滚动时没有滑动，做纯滚动，那么硬币向某个方向滚动的速度表示为：

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\end{array}\right]=r\dot{\theta }\left[\begin{array}{c}\cos \varphi \\ \sin \varphi \end{array}\right]$$

把C空间中的四个坐标写成矢量：
$$q={\left[\begin{array}{llll}{q}_1& q_2& q_3& q_4\end{array}\right]}^{\mathrm{T}}={\left[\begin{array}{l}x，y，\varphi ，\theta \end{array}\right]}^{\mathrm{T}}\in {\mathbb{R}}^2\times T^2$$
上述纯滚动约束可表示为：
$$\left[\begin{array}{cccc}1& 0& 0& -r\cos q_3\\ 0& 1& 0& -r\sin q_3\end{array}\right]\dot{q}=0$$
上式就是Pfaffian-constraints 的形式了，如下式：
$$A(q)\dot{q}=0,A(q)\in {\mathbb{R}}^{2\times 4}$$
这些约束条件是不可积的，也就是说，不存在一个可微的方程解出$A(q)$ ，这种的Pfaffian-constraints就被称为 nonholonomic constraint，这种约束降低了系统速度的维数，但没有降低C空间的维数，尽管速度受到了两个限制，但硬币可以到达四维C空间中的任意一点。

在关注完C空间之后

2.3 任务空间和工作空间

接下来将介绍与机器人配置有关的另外两个概念:任务空间和工作空间（Task Space and Workspace）。两者都与机器人的末端执行器的配置有关，而不是与整个机器人的配置有关。

对于任务空间的定义，直接采用书中的英文表述：

The task space is a space in which the robot’s task can be naturally expressed.

举个例子，如果机器人的任务是用一支笔在纸上绘图，任务空间将是 $R^2$ ，如果任务是操纵刚体，任务空间的表示为刚体的c空间，表示附着在机器人末端执行器的一个坐标系的位置和方向，这是任务空间的默认表示。 需要注意的是，如何定义任务空间是由任务样式决定的，与机器人无关。

同样，对于工作空间的定义，这里也用原书的英文表述：

The workspace is a specification of the configurations that the end-effector of the robot can reach.

工作空间的定义主要是由机器人的结构决定的，和任务空间无关。

任务空间和工作空间都涉及使用者的选择，使用者可以自行决定末端执行器的自由度。

图12 机器人工作空间图

图13 机器人工作空间图

任务空间和工作空间不同于机器人的C空间。任务空间或工作空间中的一个点可以通过多个机器人配置实现，这意味着该点可能不在某个机器人的C空间内。例如，对于一个7关节6自由度开链机器人，其末端执行器不能完全覆盖C空间。任务空间中的一些点可能是机器人根本无法到达的，然而，根据定义，工作空间中的所有点至少可以通过配置一个机器人的到达。

上述描述可能略显抽象，可以这样理解，C空间是机器人的整个拓扑结构，工作空间是机器人进行工作的拓扑结构，而任务空间是想让机器人进行工作的拓扑结构区域，但机器人受到限制可能不能工作到整个任务空间中的点。

不同于机器人的C空间。任务空间或工作空间中的一个点可以通过多个机器人配置实现，这意味着该点可能不在某个机器人的C空间内。例如，对于一个7关节6自由度开链机器人，其末端执行器不能完全覆盖C空间。任务空间中的一些点可能是机器人根本无法到达的，然而，根据定义，工作空间中的所有点至少可以通过配置一个机器人的到达。

上述描述可能略显抽象，可以这样理解，C空间是机器人的整个拓扑结构，工作空间是机器人进行工作的拓扑结构，而任务空间是想让机器人进行工作的拓扑结构区域，但机器人受到限制可能不能工作到整个任务空间中的点。