遗传算法（GA）分析总结（Matlab+C#模拟解决TSP旅行商问题）

注：该内容为个人收集总结其中也包含自己的一些理解,有点唠叨，就做个学习参考吧。

1.1、简介

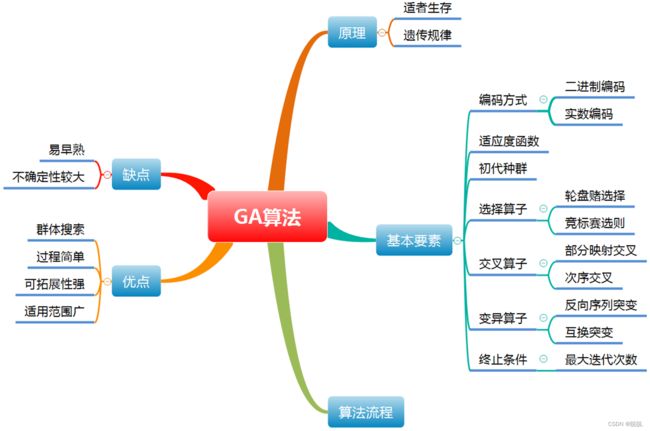
遗传算法(Genetic Algorithm，GA)由Holland教授于1975年提出，他利用种群个体之间“适者生存”的原则，仿照生物基因选择、交叉、变异的过程，给予若干次迭代，这个过程中种群会逐渐适应提前设置好的适应度函数，最终得出一个逼近最优解的优化结果。遗传算法有较好的稳健性、并行性，因为是集群搜索，使得它有较广的覆盖性，适用于全局搜索。GA算法已经广泛应用于控制、设计、人工智能、规划、图像处理、信号处理甚至建筑等领域，研究现状主要涉及三点，一是算法本身的优化与改进；二是工程优化问题的解决；三是用它在复杂的生命科学领域研究进化现象。

整体框架：

1.2、遗传算法的基本要素

生物的遗传依靠基因，基因的载体是染色体，遗传算法从宏观上看是模仿生物种群的一代一代的繁衍行为，物竞天择优胜劣汰留下的是最适应环境的个体，但在微观上其实是染色体的选择复制、交叉和变异的操作过程。提取要素，一个基本的遗传算法应该具备以下几个要素：

(1) 染色体抽象成编码，即染色体的编码方式；
(2) 物竞天择优胜劣汰的自然法则，即染色体的适应度评价函数；
(3) 一定数量的初代种群；
(4) 选择算子；
(5) 交叉算子；
(6) 变异算子；
(7) 算法的终止条件。

1.3、染色体的编码方式

对于如何编码，我们很自然的可以想到三点，即编码方式、编码长度以及解码方式。在使用遗传算法解决实际问题的时候，运用最为广发的是二进制编码和实数编码方式，根据不同的问题性质选择不同的编码方式尤为重要。

1.3.1、二进制编码

在处理如寻找一个函数在某个区间内的最大值或最小值这类过程是实数计算结果是实数显示的问题时，使用二进制编码最佳。此时的染色体编码即为使用一串二进制表示的函数的解。二进制编码的长度该如何确定？在于所求函数的定义域以及要求的精度，以下例子阐述编码长度该如何确定：

例：某函数的定义域在 范围内，搜索精度不小于P，求解二进制编码长度。由搜索精度P可知：
在范围内我们要搜索解的个数为： ；
所以需要一串能表示N个实数的二进制编码，显然编码长度为：；
即至少需要L个二进制位才能满足精度至少为P的搜索需求。编码可表示为（这里若L=10）：；
确定完了编码方式和编码长度。解码其实就是基因型到表现型的映射，解码方式不仅仅是将染色体从二进制转换为十进制的过程。L位的二进制串转换为十进制实际上存储的是 的十进制数，需要转换成范围内的十进制数，可以先求得L位二进制实际的一个十进制精度：；
于是最终解码获得的十进制数为：；

但是以这种方式编码与解码存在精度误差，因为n位二进制串只能表示2n个的十进制数，实际计算所需要搜索的解的个数N可能无法正好是2n个。例如：我们需要搜索1000个解且精度为0.01，实际上却用了10位二进制串即1024个解，如此算出的精度值约位0.009775与0.01还是存在误差的。

1.3.2、实数编码

在处理组合优化问题如典型的NP-Hard问题TSP旅行商问题时，根据问题的实际需要，我们使用实数表示不同的城市更佳，使用实数编码相比于二进制编码就简单许多，编码长度取问题中实际城市个数，一般无需解码。

1.4、适应度函数

遗传算法的适应度函数，评价个体优劣的标准，推动遗传算法进行自然选择。根据所解决的问题的不同选取合适的适应度函数十分重要，个体的适应度函数反映的是该个体适应环境的能力，适应度值高则被选择留下来的概率就越大，所以需要注意的是个体的适应度值与个体被选择的概率是成正比的，那就要求适应度值必须是非负数。当在解决求函数最值问题时，所用的适应度函数可能就是函数本身，函数值不一定是非负、绝对值大于一等情况，对应的可以灵活使用相反数、倒数来转化适应度值；对于求一个函数的非负的最大值时，可以直接将函数值为负数的个体的适应度直接设为零。

1.5、遗传算子

遗传算子包括选择、交叉和变异算子，这些算子推动了一个种群朝着更加适应环境的方向进化。由于初代种群都是随机生成的，所以它可能并不那么优秀，进化的目的就是淘汰不理想的个体，保留较优的个体继续进化下去。

1.5.1、选择算子策略

选择算子的主要功能就是为交叉算子在当前种群中挑选出一定数量的个体作为父母，也就是挑选出适应度值较高的个体。在遗传算法中选择操作并不是直接挑选适应度高的个体，自然界中好的基因也有可能被淘汰，较差的基金也有可能被遗传下来，在一定程度上保留了种群的多样性，适应度高的个体在全局来看也可能只是一个局部较高值，适应度低的个体基因里面也可能存在优秀个体的基因片段。所以选择策略也可能直接影响后续的种群的进化。目前使用最多的选择策略就是轮盘赌选择，其次是锦标赛选择策略等。下面介绍这两种选择方法：

• 轮盘赌选择
  这种选择方法类似于现实中转轮盘抽奖的过程，用随机的力道旋转轮盘，等轮盘停下来后指针所指向哪个区域就选择哪个区域。根据这个过程，我们可以提取出两个要素，一是过程随机，二是轮盘内面积更大的区域有更大的概率被选中。这正好符合进化选择，个体被选中的概率与其适应度大小成正比。
  符号定义：
  ----种群大小；
  ----种群中的个体 ；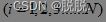
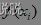  ----个体的适应度值；
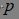  ----个体被选择的概率；
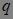  ----个体的累积概率；
  基本步骤如下：
  (1) 计算出每个个体的适应度值：；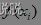
  (2) 计算出个体被选择的概率：
  (3) 计算出每个个体的累计概率：
  (4) 在[0,1]范围内生成一个伪随机数，如果则选择个体1；否则选择个体，使得；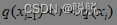
  (5) 重复(4)N次即可选择出一个新的具有N个个体的种群。
  值得注意的是通过轮盘赌选择出来的种群内会出现重复的个体，某些选择概率高的个体被选择的次数会更多，相当于让其多次交叉，充分利用了较优个体优秀的基因片段。

• 锦标赛选择
  锦标赛选择操作相对简单，但和轮盘赌选择策略一样，具有随机过程和适应度值大的个体优先的机制。具体步骤如下：
  (1) 第一步即每次从种群中随机抽出一定数量的个体，具体个数可以用占种群数量的百分之几表示；
  (2) 第二步选择其中适应度最好的个体添加到新的种群中；
  (3) 第三步重复前两步直到新的种群数量达到原来的种群数量。

1.5.2、交叉算子

选择算法产生了一个种群，但实质上种群内并没有产生新的个体，没有适应度值的变化，而交叉算子就开始真正产生新的个体，也是遗传算法中产生新个体最多的一个步骤，即两个染色体编码按照一定的交叉概率根据某种策略相互交换其他部分编码，产生两个子代染色体，分别继承了两个父代的基因，对于遗传算法的全局搜索具有重要意义。比较常用的交叉策略有次序交叉(Order Crossover)、部分映射交叉(Partial-Mapped Crossover)、子巡回交叉(Subtour Exchange Crossover)、循环交叉(Cycle Crossover)等，交叉的实质其实就是基因片段的互换，不同的交叉方式虽不同，但达到的效果基本一样。如下介绍部分映射交叉和次序交叉：

• 部分映射交叉(Partial-Mapped Crossover)
  (1) 获取两个在染色体编码个数范围内的伪随机数；
  (2) 交换这两个父染色体编码在这两个随机数范围内的基因片段，若是二进制编码，到此就结束了，但实数编码还需进行(3)(4)步；
  (3) 基因冲突检查，用交换的两个基因片段建立映射关系；
  (4) 找生成的子染色体未交换的编码部分里与交换部分相同的编码，并用映射关系替换掉这些相同编码，只替换未交换的部分，直到整个子染色体编码内不存在相同的编码为止。

对实数编码进行部分映射交叉操作如下图所示：

• 次序交叉(Order Crossover)
  (1) 获取两个在染色体编码个数范围内的伪随机数；
  (2) 取一个父染色体在这两个随机数范围内的基因片段，复制到子染色体的对应位置处；
  (3) 取另一个父染色体编码，找出刚刚复制到子代的基因片段在这一个父染色体编码里的位置，并将除这些位置里的编码外的其他编码依次复制到子染色体的空余位置中；
  (4) 到此就得到了一个子染色体，执行(1)(2)(3)一遍获得第二个子染色体，注意第(2)步应该取另一个父染色体编码。

对实数编码进行次序交叉操作如下图所示：

1.5.3、变异算子

自然界中的生物进化也存在基因突变，和遗传算法里的变异类似的是，变异的概率都很小，且都产生了新的个体。变异是为了保证种群的多样性，避免在交叉算子中可能出现的局部收敛，提高算法的全局搜索能力，遗传算法中经历交叉算子后得到的新的种群里的每一个个体都会经过一个变异概率判断是否要进行变异操作，这个概率相比于交叉概率而言一般非常小，通常取值在0.01~0.08之间。具体取值也可根据实际问题的性质、需求，经过多次测试取到一个较合适的值。

变异算子策略有反向序列突变(Reverse Sequence Mutation)、互换或相邻互换突变(Swap Mutation)等。下面介绍这两种变异方式：

• 反向序列突变
  (1) 获取两个在染色体编码个数范围内的伪随机数；
  (2) 倒序染色体在这两个随机数之间的编码，即可得一个新的染色体。

• 互换突变
  (1) 获取两个在染色体编码个数范围内的伪随机数；
  (2) 交换染色体在这两个随机数位置上的编码，即可得一个新的染色体。

1.6、终止条件

遗传算法的终止条件一般以提前设置好的迭代次数为准，也可以以两代之间的适应度值小于某个固定的值为准。

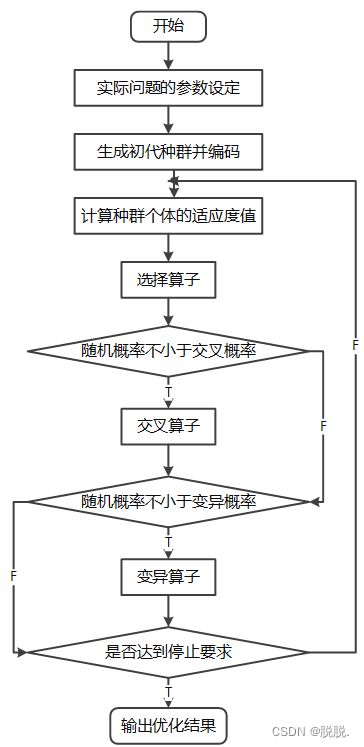
1.7、遗传算法的基本流程

1.8、遗传算法的特点

1.8.1、遗传算法的优点

(1) 第一遗传算法具有群体搜索能力，与单体搜索算法例如模拟退火算法相比，遗传算法更不容易陷入局部最优的点，因为它同时多个体处理，多个体评估，也使得遗传算法具有并行性和较好的全局搜索能力；

(2) 第二遗传算法过程简单，可以说是闭着眼睛搜索，搜索时通过适应度函数和交叉变异的概率控制搜索控制搜索方向，过程包含大量随机过程，随机生成初代种群、轮盘赌的随机过程、随机生成交叉和变异的位置，这同时也是它为何能实现全局搜索的原因，随机是避免局部最优的关键；这同时也是智能算法“智能”的体现，无论你给什么初始值，智能算法都能通过它内部的选择和训练的机制，逐渐靠近最优的结果。

(3) 第三具有可扩展性，在解决实际问题时可以和其他算法如蚁群算法、禁忌算法结合优化；

(4) 第四因为它限制条件少且大自然的优胜劣汰适者生存原则普遍存在使得遗传算法适应性广泛，可应用领域范围广。

1.8.2、遗传算法的不足

(1) 刚开始的一些优秀的个体的基因通过交叉可能会很快散播到整个种群中，容易出现早熟现象即还没全局搜索就过早收敛，基因过早同一化；

(2) 遗传算法在实际问题中选取参数大多靠多次实验或经验；

(3) 遗传算法的效率一般比传统算法效率低，因为含有大量适应度值得计算等原因；

(4) 随机的机制在一定程度上可以使遗传算法避免局部最优，提高全局搜索能力，但也使得遗传算法的不确定性增强。

2.1、组合优化问题

2.1.1、组合优化问题的描述

什么是组合优化问题？组合优化问题属于最优化问题中离散变量问题的一种，它是在一个离散的、有限集合或者可数的无限集合里寻找一个满足约束条件的最优目标解，可以是实数、集合、图形也可以是一个分组或事件的排列。当集合是有限解集时，寻找这个问题的最优解最直接的方法就是遍历整个有限集合，必然能够找到最优解，但是当问题的规模扩大，其解空间可能将会变得非常庞大，例如找到围棋下一步的最优落棋点，围棋的变化有361！种，想要遍历所有变化找到最优落棋点显然是不可能的。组合优化问题的解空间里通常还有许多局部最优的解，有些组合优化问题还有高度非线性、多维的离散的不可微的性质所以没办法使用微积分处理，精确地求解组合优化问题所需要的时间和存储空间通常让人无法接受，即“组合爆炸”，目前不存在解决组合优化问题的精确算法。

目前为止组合优化问题多使用启发式算法、智能算法解决。常见的智能算法包括进化算法和群体智能算法如遗算法、蚁群算法、鱼群算法和粒子群算法等，还有一些单体智能算法如模拟退火算法、爬山算法和禁忌搜索算法等。

常见的组合优化问题包括作业车间调度问题(Job Shop Scheduling，JSP)、旅行商问题(Traveling Salesman Problem，TSP)、车辆路径问题(Vehicle Routing Problem，VRP)等。

2.1.2、TSP旅行商问题的描述

TSP问题最早由Dantzig等人于1959年提出，描述的是给定n个城市，要求一个旅行家对每个城市有且仅访问一次后最终回到出发城市，且要求路径最短。TSP问题即求解一个最短的哈密顿回路(Hamiltonian cycle)，它不仅是一个著名的典型的组合优化问题并且还是一个NP-Hard问题，即给定一个解都无法在多项式的时间内验证其正确性。

3.1、遗传算法处理TSP问题

根据上文描述的遗传算法的思想，对处理TSP问题作以下几点设置：
(1) TSP问题以城市为路径节点，最终解为城市的序列，所以采用实数编码方式；
(2) 适应度函数选择路径长度的倒数，设计算路径长度的函数为d(x)，x为解的城市编码，则适应度函数，f(x)值越大表明该解路径长度越短；
(3) 初始种群随机生成；
(4) 选择算子采用轮盘赌选择；
(5) 交叉采用次序交叉；
(6) 变异采用反向序列突变；
(7) 终止条件选择最大迭代次数。

使用Matlab语言实现（代码见文末），参数设置如下：

att48.txt（城市坐标数据见代码块内）的城市数据共48个城市，最短哈密顿回路距离为33522；种群大小：30；交叉概率0.9；变异概率：0.05；城市数据：att48.txt；迭代次数分别取1000、2000、3000、4000、6000，遗传算法涉及的随机过程较多，优化结果并不稳定，不同迭代次数分别运行5次后取最短路径长度，所得数据结果如表所示(注：括号内为收敛于第多少代)：

最优结果路线及收敛信息如图所示：

3.1.1、结果数据分析

已知测试数据att48.txt的城市数据共48个城市，最短哈密顿回路距离为33522。根据上文各个算法对TSP问题的处理，对算法所设置的特定参数得出的结果数据进行分析，得四种算法的数据分析结果如表3-5所示（其余算法详解后续更新）：

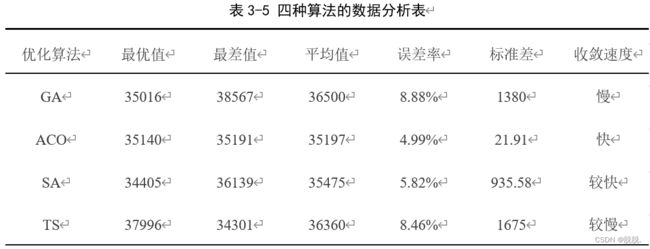
3.1.2、优化质量分析

以下结论仅通过上面的测试数据得出，存在误差，且问题不同代码编写方式不同细节处理不同都会影响算法的结果，所以确实不够严谨，仅作个人实验对比参考

1. GA算法标准差偏大，优化结果比较离散相应的方差偏大优化质量不稳定，因为它所涉及的随机过程最多以及其算法本身的性质，使得算法每次的优化结果并不稳定甚至有时相差较大，结果存在偶然性，在解决问题时，最好是多次运行然后取最优解，以上参数设置下最终优化结果误差率能在10%以内；
2. ACO算法标准差最小，所得解的值更加聚集，相应的方差也越小所以优化质量是最稳定的，多次测试最终的优化结果相差不大，误差率最小，以上参数设置下误差率能控制在5%以内；
3. SA算法标准差较高，所以它的优化结果较离散，虽然它的最优结果很好，但这并不是稳定的每次都能做出来的结果，它的误差率最终能控制在6%以内但优化质量并不稳定；
4. TS算法优化出了四个算法的最优结果，但它与SA算法和GA算法一样优化结果方差偏大导致优化质量不稳定。

3.1.3、收敛性分析

1. GA算法收敛速度偏慢，说明它并不容易跳出局部最优，可能这与它的交叉概率和变异概率相关，需要作进一步实验；
2. ACO算法收敛速度很快一般在50代以内完全收敛，ACO算法由于刚开始优化缺少信息素的正反馈所以算法前期收敛较慢，但后期信息素正反馈逐步增强算法会很快收敛；
3. SA算法从以上的实验数据来看收敛较快一般都能在500代以内完全收敛，SA算法由于Metropolis准则，温度越低接受较差解的概率可能越低，所以算法在前期反而收敛更快，后期收敛较慢；
4. TS算法通过禁忌表的记忆机制虽然可以避免很多不必要的循环，但它更新最优解的方法主要是特设准则，能否找到满足特设准则的解，那也要看当前解的邻域解的质量如何，所以TS算法的收敛速度并没有多优秀。

3.1.4、Matlab代码模拟处理TSP

main.m

tic
Citys=[3245.00 3305.00;
        3484.00 2829.00;
        3023.00 1942.00;
        3082.00 1644.00;
        1916.00 1569.00;
        1633.00 2809.00;
        1112.00 2049.00;
        10.00 2676.00;
        23.00 2216.00;
        401.00 841.00;
        675.00 1006.00;
        2233.00 10.00;
        3177.00 756.00;
        4608.00 1198.00;
        4985.00 140.00;
        6107.00 669.00;
        6101.00 1110.00;
        5530.00 1424.00;
        5199.00 2182.00;
        4612.00 2035.00;
        4307.00 2322.00;
        4706.00 2674.00;
        5468.00 2606.00;
        5989.00 2873.00;
        6347.00 2683.00;
        6271.00 2135.00;
        6898.00 1885.00;
        6734.00 1453.00;
        7265.00 1268.00;
        7392.00 2244.00;
        7545.00 2801.00;
        7509.00 3239.00;
        7462.00 3590.00;
        7573.00 3716.00;
        7541.00 3981.00;
        7608.00 4458.00;
        7762.00 4595.00;
        7732.00 4723.00;
        7555.00 4819.00;
        7611.00 5184.00;
        7280.00 4899.00;
        7352.00 4506.00;
        7248.00 3779.00;
        6807.00 2993.00;
        6426.00 3173.00;
        5900.00 3561.00;
        5185.00 3258.00;
        4483.00 3369.00;
];

[CitysNum,py] = size(Citys);
popsize = 30; % 初始种群大小
gen = 1;
genMax = 3000;  % 最大代数
crossProb = 0.9; % 交叉概率
muteProb = 0.05; % 变异概率
pop = zeros(popsize, CitysNum); % 初始种群
newpop = zeros(popsize, CitysNum); % 新的种群
distances=zeros(CitysNum,CitysNum);%用来记录任意两个城市之间的距离
L_best = inf.*ones(genMax,1);% 每一代的最短距离
R_best = zeros(genMax, CitysNum); % 每一代的最佳路径

for i = 1 : CitysNum
        for j = 1:CitysNum
            distances(i, j) = ((Citys(i,1) - Citys(j,1))^2 + (Citys(i,2) - Citys(j,2))^2)^0.5;
        end
end
 
% 随机产生初始种群
for i = 1 : popsize
    pop(i,:) = randperm(CitysNum);
end
[~, cumulativeProbs] = cumsumProbability(pop, distances); % 计算种群每条染色体的累计概率
 
by = 0;
jc = 0;
while gen <= genMax
   for j = 1 : 2 : popsize
      selectedChromos = select(cumulativeProbs);  % 选择操作，选出两条需要交叉编译的染色体，即父亲母亲
      [crossedChromos,jc] = cross(pop, selectedChromos, crossProb,jc);  % 交叉操作，返回交叉后的染色体
      [newpop(j, :),by] = mut(crossedChromos(1, :),muteProb,by);  % 对交叉后的染色体进行变异操作 
      [newpop(j + 1, :),by] = mut(crossedChromos(2, :), muteProb,by); % 对交叉后的染色体进行变异操作    
   end
   pop = newpop;  %产生了新的种群
   [fitnessValue, cumulativeProbs] = cumsumProbability(pop, distances);  % 计算新种群的适应度
   % 记录当前代最好和平均的适应度
   if (gen >= 2) && (L_best(gen - 1,1) < 1.0/fitnessValue(1))
      fitnessValue(1) = 1.0/L_best(gen - 1,1);
      pop(1, :) = R_best(gen - 1, :);
   end
   [fmax, nmax] = max(fitnessValue); % 因为计算适应度时取距离的倒数，这里面取最大的倒数，即最短的距离
   L_best(gen,1) = 1 / fmax;   
   bestChromo = pop(nmax, :);  % 前代最佳染色体，即对应的路径
   R_best(gen, :) = bestChromo; % 记录每一代的最佳染色体

%一边运行一边显示，便于观察，速度会很慢,不建议使用以下注释的代码
%     figure(1);
%     for i=1:(CitysNum-1)
%         plot([Citys(R_best(gen,i),1),Citys(R_best(gen,i+1),1)],[Citys(R_best(gen,i),2),Citys(R_best(gen,i+1),2)],'bo-');
%         hold on;
%     end
%     plot([Citys(R_best(gen,CitysNum),1),Citys(R_best(gen,1),1)],[Citys(R_best(gen,CitysNum),2),Citys(R_best(gen,1),2)],'ro-');
% 
%     xlabel('城市位置横坐标')
%     ylabel('城市位置纵坐标')
%     title(['迭代次数:',int2str(gen),'最短路径：',num2str(L_best(gen,1))]);
%     hold off;
%     pause(0.001);
% 
%     figure(2);
%     plot(L_best);
%     title('路径长度变化曲线');
%     xlabel('迭代次数');
%     ylabel('路径长度数值');
 
   gen = gen + 1;
end
%最后一次性显示结果，速度更快
[bestValue,index] = min(L_best);
figure(1);
for i=1:CitysNum-1
        plot([Citys(R_best(index,i),1),Citys(R_best(index,i+1),1)],[Citys(R_best(index,i),2),Citys(R_best(index,i+1),2)],'bo-');    % 画出两点的连线
        hold on;
end
    plot([Citys(R_best(index,CitysNum),1),Citys(R_best(index,1),1)],[Citys(R_best(index,CitysNum),2),Citys(R_best(index,1),2)],'ro-');% 画出最后一点与出发点的连线（红色）
    xlabel('城市位置横坐标')
    ylabel('城市位置纵坐标')
    title(['迭代次数:',int2str(gen-1),' 优化最短距离:',num2str(bestValue)]);
%收敛情况
figure(2);
plot(L_best, 'r');  
hold on;
grid;
title('路径长度变化曲线');
xlabel('迭代次数');
ylabel('路径长度数值');
legend('最优解', '平均解');
fprintf('遗传算法得到的最短距离: %.2f\n', bestValue);
fprintf('遗传算法得到的最短路线');
disp("变异了"+by+"次");
disp("交叉了"+jc+"次");
toc

CalRouteLength.m

% 计算一条染色体的适应度
% chromo 为一条染色体，即一条路径
function chromoValue = CalRouteLength(distances, chromo)
RouteLength = 0;
n = size(chromo, 2); % 染色体的长度
for i = 1 : (n - 1)
    RouteLength = RouteLength + distances(chromo(i), chromo(i + 1));
end
RouteLength = RouteLength + distances(chromo(n), chromo(1));
chromoValue = RouteLength;
end

cross.m

% “交叉”操作
function [crossedChromos,jc1] = cross(pop, selectedChromoNums, crossProb,jc)
jc1 = jc;
length = size(pop, 2); % 染色体的长度
crossProbc = crossMuteOrNot(crossProb);  %根据交叉概率决定是否进行交叉操作，1则是，0则否
%先获取父母染色体
crossedChromos(1,:) = pop(selectedChromoNums(1), :);
crossedChromos(2,:) = pop(selectedChromoNums(2), :);
if crossProbc == 1
    %随机产生交叉位
   c1 = round(rand * (length - 2)) + 1;  %在[1,popsize - 1]范围内随机产生一个交叉位 c1
   c2 = round(rand * (length - 2)) + 1;  
   chb1 = min(c1, c2);
   chb2 = max(c1,c2);
   % 两条染色体 chb1 到 chb2 之间互换位置
   middle = crossedChromos(1,chb1+1:chb2); 
   crossedChromos(1,chb1 + 1 : chb2)= crossedChromos(2, chb1 + 1 : chb2);
   crossedChromos(2,chb1 + 1 : chb2)= middle;
   for i = 1 : chb1 % 看交叉后，染色体上是否有相同编码的情况（路径上重复出现两个城市）。若有，则该编码不参与交叉
       while find(crossedChromos(1,chb1 + 1: chb2) == crossedChromos(1, i))
           location = find(crossedChromos(1,chb1 + 1: chb2) == crossedChromos(1, i));%找到这个在crossedChromos(1,chb1 + 1: chb2)段重复的位置
           y = crossedChromos(2,chb1 + location);
           crossedChromos(1, i) = y;
       end
       while find(crossedChromos(2,chb1 + 1 : chb2) == crossedChromos(2, i))
           location = find(crossedChromos(2, chb1 + 1 : chb2) == crossedChromos(2, i));
           y = crossedChromos(1, chb1 + location);
           crossedChromos(2, i) = y;
       end
   end
   for i = chb2 + 1 : length
       while find(crossedChromos(1, 1 : chb2) == crossedChromos(1, i))
           location = logical(crossedChromos(1, 1 : chb2) == crossedChromos(1, i));
           y = crossedChromos(2, location);
           crossedChromos(1, i) = y;
       end
       while find(crossedChromos(2, 1 : chb2) == crossedChromos(2, i))
           location = logical(crossedChromos(2, 1 : chb2) == crossedChromos(2, i));
           y = crossedChromos(1, location);
           crossedChromos(2, i) = y;
       end
   end
   jc1 = jc+1;
end
end

crossMuteOrNot.m

% 根据变异或交叉概率，返回一个 0 或 1 的数
function crossProbc = crossMuteOrNot(crossMutaProb)
test(1: 100) = 0;
l = round(100 * crossMutaProb);
test(1 : l) = 1;
n = round(rand * 99) + 1;
crossProbc = test(n);
end

cumsumProbability.m

function [fitvalues, cumulativeProbs] = cumsumProbability(pop, distances)
popsize = size(pop, 1);  % 读取种群大小
fitvalues = zeros(popsize, 1);
for i = 1 : popsize
    fitvalues(i) = CalRouteLength(distances, pop(i, :));  % 计算每条染色体的路径长度
end
fitvalues = 1./fitvalues'; % 距离越小，适应度值越大，被选取的概率越高

% 根据个体的适应度计算其被选择的概率
fsum = 0;
for i = 1 : popsize
    % 乘以15次方的原因是让好的个体被选取的概率更大（因为适应度取距离的倒数，若不乘次方，则个体相互之间的适应度差别不大），换成一个较大的数也行
    fsum = fsum + fitvalues(i)^15;   
end
 
% 计算单个概率
probs = zeros(popsize, 1);
for i = 1: popsize
    probs(i) = fitvalues(i)^15 / fsum;
end
 
% 计算累积概率
%cumulativeProbs = zeros(popsize,1);
% cumulativeProbs(1) = probs(1);
% for i = 2 : popsize
%     cumulativeProbs(i) = cumulativeProbs(i - 1) + probs(i);
% end
cumulativeProbs = cumsum(probs);
cumulativeProbs = cumulativeProbs';
end

mut.m

%“变异”操作
% choromo 为一条染色体
function [snnew,by1] = mut(chromo,muteProb,by)
by1 = by;
length = size(chromo, 2); % 染色体的的长度
snnew = chromo;
muteProbm = crossMuteOrNot(muteProb);  % 根据变异概率决定是否进行变异操作，1则是，0则否
if muteProbm == 1
    c1 = round(rand*(length - 2)) + 1;  % 在 [1, popsize - 1]范围内随机产生一个变异位
    c2 = round(rand*(length - 2)) + 1;  % 在 [1, popsize - 1]范围内随机产生一个变异位
    chb1 = min(c1, c2);
    chb2 = max(c1, c2);
    x = chromo(chb1 + 1 : chb2);
    snnew(chb1 + 1 : chb2) = fliplr(x); % 变异，则将两个变异位置的染色体倒转
    by1 = by+1
end
end

select.m

% 选择操作，返回所选择染色体在种群中对应的位置
function selectedChromoNums = select(cumulativeProbs)
selectedChromoNums = zeros(2, 1);
% 从种群中选择两个个体
for i = 1 : 2
   r = rand;  % 产生一个随机数
   prand = cumulativeProbs - r;
   j = 1;
   while prand(j) < 0
       j = j + 1;
   end
   selectedChromoNums(i) = j; % 选中个体的序号
   %如果使两次选择的个体不同
%    if i == 2 && j == selectedChromoNums(i - 1)    % 若相同就再选一次
%        r = rand;  % 产生一个随机数
%        prand = cumulatedPro - r;
%        j = 1;
%        while prand(j) < 0
%            j = j + 1;
%        end
%    end
end
end

4.1、C#模拟

GA算法处理TSP问题实验界面：

遗传算法处理TSP问题实验界面中，参数设置开始有预设默认值，点击文本框会自动清空随后再自己输入；数据文件选择后左边会显示数据文件的绝对地址；算法运行时使用此地址找到文件并转化成以二维数组存储的double类型数据；选择设置为全局TSP问题城市数据则将会把此数据文件的绝对地址发送给全局数据地址变量，其他算法自动使用此变量存储的地址，当取消勾选，即其他城市无法使用GA的城市数据；运行时间显示为分：秒：毫秒；意味着最多只能计时60分钟；每次运行只要不点击最下方的清空结果，就会记录之前运行的结果，并且在左边文本框显示试验次数。

结果显示，左起第一个ListView显示的是最近一次实验每次迭代的结果数据，包括迭代次数、城市序号、路径长度，下方的ListView显示的是之前所有结果的数据；这里遗传算法所显示的数据有：最佳优化路径的城市序号、路径长度、在第几代完成收敛、交叉操作完成了多少次、变异操作完成了多少次。最右边的ListView展示最近一次实验最佳优化路径的城市序号和城市位置的映射。

开发环境使用Visual Studio 2019(vs2019)、开发语言C#以及.NET Framework Windows窗体应用开发类库。
VS项目文件链接，有需要的可以作学习参考：C#仿真程序资源