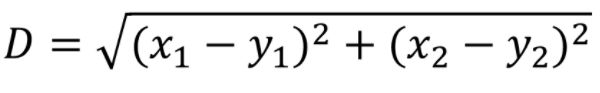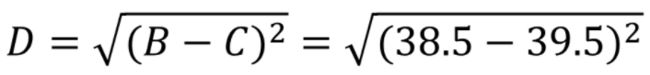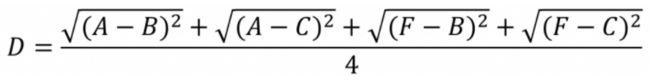层次聚类汇总

层次聚类(Hierarchical Clustering)，计算不同类别数据点间的相似度创建一棵有层次的嵌套聚类树。在聚类树中，不同类别的原始数据点是树的最低层，树的顶层是一个聚类的根节点。创建聚类树有自下而上合并和自上而下分裂两种方法。

凝聚的层次聚类：AGNES算法(AGglomerative NESting) → 自底向上 的策略。

初始每个对象为一个簇，这些簇根据某些准则合并，两个簇间的距离可以由这两个不同簇中距离最近的数据点的相似度来确定；聚类的合并过程反复进行直到所有的对象满足簇数目。

分裂的层次聚类：DIANA算法(DIvisive ANALysis) → 自顶向下 的策略。

初始将所有对象置于一个簇中，按照某种既定的规则逐渐细分为越来越小的簇(比如最大的欧式距离)，直到达到某个终结条件(簇数目或者簇距离达到阈值)。

层次聚类常常使用称作 树状图 的类似于树的图显示，显示簇-子簇联系和簇合并（凝聚）或分类的次序。对于二维点的集合，层次聚类也可以使用嵌套簇图表示。

基本凝聚层次聚类算法

• 计算邻近的簇距离
• 合并最接近的两个簇
• 更新邻近距离矩阵，反映新的簇与原来的簇之间的邻近性
• 直到仅剩下一个簇

计算两个簇之间的邻近性的三种方法：

• 最小距离（MIN）：两个聚簇中最近的两个样本之间的距离(single/word-linkage聚类法)，最终得到模型容易形成链式结构

• 最大距离(MAX)：两个聚簇中最远的两个样本的距离(complete-linkage聚类法)，如果存在异常值，那么构建可能不太稳定

• 组平均：两个聚簇中样本间两两距离的平均值(average-linkage聚类法)，两个聚簇中样本间两两距离的中值(median-linkage聚类法)

• 簇用质心代表，则不同的簇邻近度定义就更容易，使用质心时，簇的邻近度一般定义为簇质心之间的邻近度。
• Ward 方法，假定簇用其质心代表，但使用两个簇的SSE增加来度量两个簇之间的邻近性，类似于 K均值 ，Ward 方法也试图最小化点到其簇质心的距离的平方和。
• 对于 Ward 方法，两个簇的邻近度定义为两个簇合并时导致的平方误差的增量。目标函数与K-means相同。当两个点之间的邻近度取距离的平方时，Ward 方法与 组平均 类似。

欧氏距离：

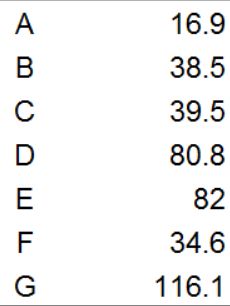
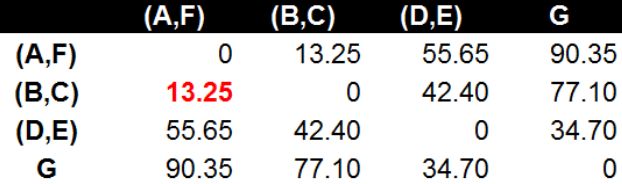
例如：有如下数据，B和C间距离为D，是两点间最小的，合并为一组；据需计算点间距离(相似度)，计算组合数据点(B,C)与其他数据点的如A点的距离时，分别计算B到A和C到A的距离均值。

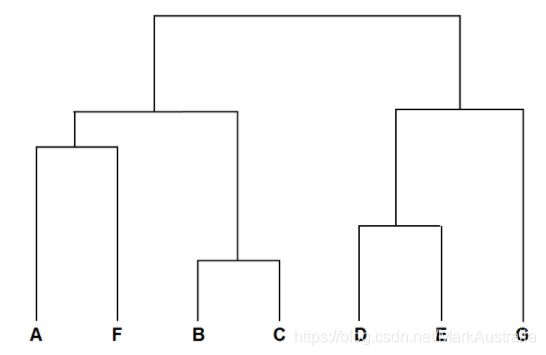
通过计算，组合如下：(A,F), (B,C),(D,E),G

使用Average Linkage计算(A,F),(B,C)间距离

 

（D,E）与G距离最小，得到组合数据点(A,F,B,C)和(D,E,G)；这是聚类树的最顶层的两个数据点。

构建的树结构如下：

层次聚类的优点：可一次性得到整个聚类的过程，即上面的聚类树，想分多少个cluster都可以直接根据树结构来得到结果，改变 cluster数目不需要再次计算数据点的归属。

层次聚类缺点：计算量比较大，每次都要计算多个cluster内所有数据点的两两距离，属于是贪心算法，得到局部最优，不一定是全局最优，可加入随机效应解决。

基于距离的聚类(如划分聚类、层次聚类)，一般很难发现非凸形状的集合或大小差别很大的集合。

import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.cluster import AgglomerativeClustering  # 层次聚类
from sklearn.cluster import KMeans

if __name__ == "__main__":
    # 构造数据
    X, y_true = make_moons(n_samples=1000, noise=0.05)
    plt.scatter(X[:, 0], X[:, 1], c=y_true)
    plt.show()

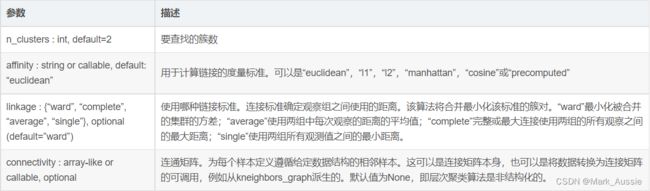
    ward = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward', compute_full_tree='false').fit(X)
    kmeans = KMeans(init='k-means++', n_clusters=2, random_state=8).fit(X)

    plt.scatter(X[:, 0], X[:, 1], c=ward.labels_)
    plt.show()

    plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_)
    plt.show()

• 对于 Ward 方法，使用的是方差，对球形数据的效果不错，但是对月牙形数据就不好了；
• 对于complete方法，使用的是最大值，对于球形数据基本不行，对于月牙形效果很好，但是假如噪声后，效果就不行，可见此方法受噪声的影响；
• 对于 average 方法，使用的是平均值，效果和最大值方法一样。

层次聚类优化算法

BIRCH 算法(平衡迭代削减聚类法)：用于欧几里得向量空间数据，即平均值有意义的数据。

BIRCH 能够用一遍扫描有效地对这种数据进行聚类，并可以使用附加的扫描改进聚类。

BIRCH 还能有效地处理离群点。

BIRCH 基于聚类特征和聚类特征树的概念。基本思想是：数据点的簇用三元组 (N, LS, SS) 表示：

•  N 是簇中点的个数
•  LS 是点的线性和
•  SS 是点的平方和

BIRCH 算法通过构建满足 分枝因子和簇直径限制 的聚类特征树来求聚类，聚类特征树其实是一个具有两个参数分枝因子和类直径的高度平衡树；分枝因子规定了树的每个节点的子女的最多个数，而类直径体现了对这一类点的距离范围；非叶子节点为它子女的最大特征值；聚类特征树的构建可以是动态过程的，可以随时根据数据对模型进行更新操作。

优缺点：

        适合大规模数据集，线性效率；

        只适合分布呈凸形或者球形的数据集、需要给定聚类个数和簇之间的相关参数；

CURE 算法(使用代表点的聚类法)：初始把每个数据点看成一类，合并距离最近的类直至类个数为所要求的个数为止，但是和 AGNES 算法的区别是：取消了使用所有点或用中心点+距离来表示一个类，而是从每个类中抽取固定数量、分布较好的点作为此类的代表点，并将这些代表点乘以一个适当的收缩因子，使它们更加靠近类中心点。

CURE 使用簇中的多个代表点来表示一个簇：

• 第一个代表点选择离簇中心点最远的点
• 其余的点选择离所有已经选取的点最远的点
• 理论上，这些点捕获了簇的几何形状

代表点的收缩特性可以调整模型可以匹配那些非球形的场景，而且收缩因子的使用可以减少噪音对聚类的影响。

优缺点：

        能够处理非球形分布的应用场景;

        采用随机抽样和分区的方式可以提高算法的执行效率;

参考：

层次聚类算法的原理及实现Hierarchical Clustering (bluewhale.cc)

层次聚类算法_起点站的博客-CSDN博客_层次聚类算法