ZOJ-3615 Party of 8g 最大点权独立集

　　题目链接：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=3182

　　最大点权独立集。算法是建立网络流模型，加源汇点s和t，源点s向x集合中的每个点建立边，容量为点的权值，y集合的每个点向汇t建立边，容量为点的权值，然后x集合和y集合相关联的点建立边，容量为INF。最后求最小割就可以了，所有点的权值之和减去最小割就是最大权值，独立点集就是全集减去最小割的点集。为什么是这样的呢？其实每条增广路代表的就是一条相关联的边，找到一条增广路我们就删除一个点，如果找不到增广路了，那么剩下的点就是独立的了。由于是最小割，那么删除的点集的权值就是最小的，即剩下的是最大权。这里还要求求出最小割点集，在做完最大流后在残余网络上求一次bfs就可以了，能经过的点就是S集合的，否则就是T集合的。我开始以为在bfs时只要边的容量为零，边能通过且点没有经过，那么此边就是割边，后来发现还是错了。看一个样例：

                       

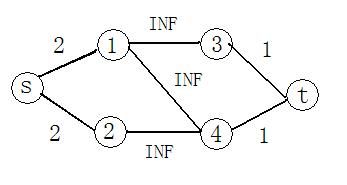
  那么这里最小割显然是3-t，4-t，如果按上面方法求，就错了，因为那个没有考虑反向边，所以应该做次bfs后根据S集合和T集合判断。

  1 //STATUS:C++_AC_450MS_2948KB

  2 #include<stdio.h>

  3 #include<stdlib.h>

  4 #include<string.h>

  5 #include<math.h>

  6 #include<iostream>

  7 #include<string>

  8 #include<algorithm>

  9 #include<vector>

 10 #include<queue>

 11 #include<stack>

 12 #include<map>

 13 using namespace std;

 14 #define LL long long

 15 #define pii pair<int,int>

 16 #define Max(a,b) ((a)>(b)?(a):(b))

 17 #define Min(a,b) ((a)<(b)?(a):(b))

 18 #define mem(a,b) memset(a,b,sizeof(a))

 19 #define lson l,mid,rt<<1

 20 #define rson mid+1,r,rt<<1|1

 21 const int MAX=210,INF=0x3f3f3f3f;

 22 const LL LLNF=0x3f3f3f3f3f3f3f3fLL;

 23 

 24 struct Edge{

 25     int u,v,cap;

 26 }e[MAX*MAX*4];

 27 

 28 int first[MAX],next[MAX*MAX*4],p[MAX],cur[MAX],w[MAX],num[MAX],d[MAX];

 29 int n,n1,n2,m,mt,s,t;

 30 

 31 void adde(int a,int b,int val){

 32     e[mt].u=a,e[mt].v=b,e[mt].cap=val;

 33     next[mt]=first[a],first[a]=mt++;

 34     e[mt].u=b,e[mt].v=a,e[mt].cap=0;

 35     next[mt]=first[b],first[b]=mt++;

 36 }

 37 

 38 int augment()

 39 {

 40     int x=t,a=INF;

 41     while(x!=s){

 42         a=Min(a,e[p[x]].cap);

 43         x=e[p[x]].u;

 44     }

 45     x=t;

 46     while(x!=s){

 47         e[p[x]].cap-=a;

 48         e[p[x]^1].cap+=a;

 49         x=e[p[x]].u;

 50     }

 51     return a;

 52 }

 53 

 54 int isap()

 55 {

 56     int i,x=s,ok,flow=0,min;

 57     mem(d,0);mem(num,0);

 58     num[0]=t+1;

 59     for(i=0;i<=t;i++)cur[i]=first[i];

 60     while(d[s]<=t){

 61         if(x==t){

 62             flow+=augment();

 63             x=s;

 64         }

 65         ok=0;

 66         for(i=cur[x];i!=-1;i=next[i]){

 67             if(e[i].cap && d[x]==d[e[i].v]+1){

 68                 ok=1;

 69                 p[e[i].v]=i;

 70                 cur[x]=i;

 71                 x=e[i].v;

 72                 break;

 73             }

 74         }

 75         if(!ok){

 76             min=t;

 77             for(i=first[x];i!=-1;i=next[i])

 78                 if(e[i].cap && d[e[i].v]<min)min=d[e[i].v];

 79             if(--num[d[x]]==0)break;

 80             num[d[x]=min+1]++;

 81             cur[x]=first[x];

 82             if(x!=s)x=e[p[x]].u;

 83         }

 84     }

 85     return flow;

 86 }

 87 

 88 void bfs()

 89 {

 90     int i,x;

 91     mem(d,0);

 92     queue<int> q;

 93     q.push(s);

 94     d[s]=1;

 95     while(!q.empty()){

 96         x=q.front();q.pop();

 97         for(i=first[x];i!=-1;i=next[i])

 98             if(e[i].cap && !d[e[i].v]){

 99                 d[e[i].v]=1;

100                 q.push(e[i].v);

101             }

102     }

103 }

104 

105 int main()

106 {

107   //  freopen("in.txt","r",stdin);

108     int i,a,b,all,mincut,cou1,cou2,flag;

109     while(~scanf("%d%d%d",&n1,&n2,&m))

110     {

111         n=n1+n2;

112         t=n+1;

113         cou1=cou2=mincut=all=s=mt=0;

114         mem(first,-1);

115 

116         for(i=1;i<=n1;i++){

117             scanf("%d",&a);

118             adde(s,i,a);

119             all+=w[i]=a;

120         }

121         for(;i<=n;i++){

122             scanf("%d",&a);

123             adde(i,t,a);

124             all+=w[i]=a;

125         }

126         for(i=0;i<m;i++){

127             scanf("%d%d",&a,&b);

128             adde(a,n1+b,INF);

129         }

130 

131         mincut=isap();

132         bfs();

133 

134         for(i=1;i<=n;i++)

135             if(d[i] && i<=n1)cou1++;

136             else if(!d[i] && i>n1)cou2++;

137         printf("%d %d %d\n",all-mincut,cou1,cou2);

138         for(i=1,flag=1;i<=n1;i++)

139             if(d[i]){

140                 if(flag){printf("%d",i);flag=0;}

141                 else printf(" %d",i);

142             }

143         putchar('\n');

144         for(flag=1;i<=n;i++)

145             if(!d[i]){

146                 if(flag){printf("%d",i-n1);flag=0;}

147                 else printf(" %d",i-n1);

148             }

149         putchar('\n');

150     }

151     return 0;

152 }