Theano入门-导数

Theano里的导数

计算梯度

现在让我们做稍微更复杂的任务：创建一个计算y对参数x的导数的函数。使用T.grad计算导数。例如，我们计算x^2对x的导数。注意：d(x^2)/dx = 2x。
下面是计算梯度的代码：

>>> from theano import pp
>>> x = T.dscalar('x')
>>> y = x ** 2
>>> gy = T.grad(y, x)
>>> pp(gy)  # print out the gradient prior to optimization
'((fill((x ** 2), 1.0) * 2) * (x ** (2 - 1)))'
>>> f = function([x], gy)
>>> f(4)
array(8.0)
>>> f(94.2)
array(188.40000000000001)

在这个例子，我们能从pp(gy)看到正确地计算了符号的梯度。fill((x ** 2), 1.0)意思是创建一个大小与x ** 2一样的矩阵，并填充1.0。

注意：优化器简化符号梯度的表达式。我们可以通过挖掘已编译的函数的内部属性看到。

pp(f.maker.fgraph.outputs[0])
'(2.0 * x)'

优化之后，只有一个计算输入的2倍的apply结点在图的左侧。

我们也可以计算复杂表达式的梯度，比如上面定义的logistic函数。结果是logistic的梯度：$ds(x)/dx = s(x) \cdot (1 - s(x))$。

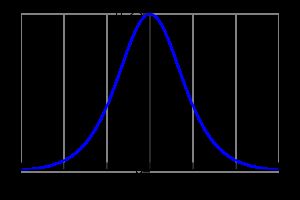
logistic的梯度的图形，x在x轴，ds(x)/dx在y轴。

>>> x = T.dmatrix('x')
>>> s = T.sum(1 / (1 + T.exp(-x)))
>>> gs = T.grad(s, x)
>>> dlogistic = function([x], gs)
>>> dlogistic([[0, 1], [-1, -2]])
array([[ 0.25      ,  0.19661193],
	   [ 0.19661193,  0.10499359]])

通常，对任何标量表达式s，T.grad(s, w)计算$\frac{\partial s}{\partial w}$。这样，Theano可以用于有效地计算符号微分（T.grad的返回的表达式会在编译时优化），即使函数有多个输入。（automatic differentiation查看符号微分的描述）

注意：T.grad的第二个参数可以为一个列表，则输出也将是一个列表。返回的梯度与T.grad的第二个参数的一致。T.grad的第一个参数必须是一个scalar（大小为1的tensor）。关于T.grad的参数的语义学的更多信息和实现的细节，查看库的this这节。

微分的内部工作的额外的信息可以在更高级的入门Extending Theano找到。

计算Jacobian

在Theano语法中，术语jacobian表示为函数的输出对输入的一阶导组成的tensor。（这只是数学中称为雅克布矩阵的一般化。）Theano实现theano.gradient.jacobian()宏做所有计算Jacobian的需要的事。下面的文字说明怎么样手工地计算。

为了手动地计算一些函数y对参数x的Jacobian，我们需要使用scan。我们需要做的是循环y的每一项，并计算y[i]对x的梯度。

注意：scan在Theano里是一个一般的操作，允许以符号的方式写各种递归的方程。虽然创建符号循环是一个困难的任务，scan所做的能力就是提高性能。在这个入门中，我们不久将返回到scan中。

>>> x = T.dvector('x')
>>> y = x ** 2
>>> J, updates = theano.scan(lambda i, y,x : T.grad(y[i], x), sequences=T.arange(y.shape[0]), non_sequences=[y,x])
>>> f = function([x], J, updates=updates)
>>> f([4, 4])
array([[ 8.,  0.],
	   [ 0.,  8.]])

代码中我们所做的是使用T.arange生成一个从0到y.shape[0]的int型序列。然后我们通过循环这个序列，每次我们计算y[i]对x的梯度。scan自动连接所有这些行，生成一个与Jacobian相应的矩阵。

注意：关于T.grad这里有几个要注意的陷阱。其中一个是，不能把上面的Jacobian表达式改为theano.scan(lambda y_i,x: T.grad(y_i,x), sequences=y, non_sequences=x)，即使从scan文档是合理的。理由是y_i不再是一个x的函数，而y[i]仍然是。

计算Hessian

在Theano里，术语Hessian有着通常的数学领域：由带scalar输入和向量输出的函数的二阶偏导数。Theano实现theano.gradient.hessian()宏，做计算Hessian需要的所有事。下面的文字解释如何手动地计算。

你可以像Jacobian一样地手动地计算Hessian。唯一的不同是使用T.grad(cost,x)替换计算Jacobian的某些表达式y，cost试一些标量。

>>> x = T.dvector('x')
>>> y = x ** 2
>>> cost = y.sum()
>>> gy = T.grad(cost, x)
>>> H, updates = theano.scan(lambda i, gy,x : T.grad(gy[i], x), sequences=T.arange(gy.shape[0]), non_sequences=[gy, x])
>>> f = function([x], H, updates=updates)
>>> f([4, 4])
array([[ 2.,  0.],
	   [ 0.,  2.]])

Jacobian乘以一个向量

有时我们需要使用Jacobian乘上向量表示算法，或向量乘上Jacobian。相比计算Jacobian，然后做乘积，这有计算想要的结果并且避免计算Jacobian的方法。这可以带来有效的性能收益。这样的算法的一个描述可以在这里找到：

• Barak A. Pearlmutter, “Fast Exact Multiplication by the Hessian”, Neural Computation, 1994

当我们大体上想让Theano为我们自动地识别这样的模式，实际上，以普通方法实现这样的优化是非常困难的。因此，我们提供特殊的函数专门做这个。

R-运算符

R运算符被创建去计算Jacobian和向量的乘积，也就是$\frac{\partial f(x)}{\partial x} v$。公式可以扩展到即时x是一个矩阵，或者普通的tensor，或者在Jacobian是一个tensor下，乘积变成某种tensor的乘积。因为，实际上，我们结束需要使用权值矩阵计算这样的表达式，Theano支持更通用的操作形式。为了计算表达式y对x的R运算，Jacobian乘以v，你需要做下面相似的运算：

>>> W = T.dmatrix('W')
>>> V = T.dmatrix('V')
>>> x = T.dvector('x')
>>> y = T.dot(x, W)
>>> JV = T.Rop(y, W, V)
>>> f = theano.function([W, V, x], JV)
>>> f([[1, 1], [1, 1]], [[2, 2], [2, 2]], [0,1])
array([ 2.,  2.])

实现R运算符的运算列表。

L-运算符

与R-运算符类似，L-运算符计算一个行向量乘以Jacobian。数学公式：$v \frac{\partial f(x)}{\partial x}$。L-运算符也支持普通的tensors(不仅仅向量)。同样地，可以实现为下面的：

>>> W = T.dmatrix('W')
>>> v = T.dvector('v')
>>> x = T.dvector('x')
>>> y = T.dot(x, W)
>>> VJ = T.Lop(y, W, v)
>>> f = theano.function([v,x], VJ)
>>> f([2, 2], [0, 1])
array([[ 0.,  0.],
	   [ 2.,  2.]])

注意：v，计算的关键是区别L-运算符和R-运算符。对于L-运算符，计算的关键是需要有像输出一样的形状，而R-操作是与输入同样的形状。此外，两个运算符的结果也是不同的。L-运算符的结果是与输入同样大小的，而R-运算符是与输出同样大小的。

Hessian乘上向量

如果你需要计算Hessian乘以向量，可以利用上面定义的运算符去做比实际计算额外的Hessian更有效地计算，然后执行乘积。因为Hessian矩阵是对称的，可以有两种选择获取同样的结果，两种选择可能显示出不同的性能。因此，我们建议在使用其中一个时先做性能分析：

>>> x = T.dvector('x')
>>> v = T.dvector('v')
>>> y = T.sum(x ** 2)
>>> gy = T.grad(y, x)
>>> vH = T.grad(T.sum(gy * v), x)
>>> f = theano.function([x, v], vH)
>>> f([4, 4], [2, 2])
array([ 4.,  4.])

或者，使用R-运算符：

>>> x = T.dvector('x')
>>> v = T.dvector('v')
>>> y = T.sum(x ** 2)
>>> gy = T.grad(y, x)
>>> Hv = T.Rop(gy, x, v)
>>> f = theano.function([x, v], Hv)
>>> f([4, 4], [2, 2])
array([ 4.,  4.])

最后的关键点

• grad函数符号运算的：接受和返回Theano变量。
  
• grad可以反复地运用，因此好比一个宏。
  
• 标量的costs只能直接地被grad使用。数组被重复的应用使用。
  
• 内建的函数允许有效地计算向量乘以Jacobian或者向量乘以Hessian。
  
• 有效地计算完整的Jacobian和Hessian或者Jacobian与向量的乘积的优化正在做的过程中。