数学建模-相关性分析（Matlab）

 注意：代码文件仅供参考，一定不要直接用于自己的数模论文中
国赛对于论文的查重要求非常严格，代码雷同也算作抄袭
如何修改代码避免查重的方法：https://www.bilibili.com/video/av59423231   //清风数学建模

一、基础知识

1.皮尔逊相关系数

连续数据、正态分布、线性关系三者同时满足优先用。

一般处理这种问题：如中学生体测成绩考察相关性
​​​​

 统计描述：

%% 统计描述
MIN = min(Test);  % 每一列的最小值
MAX = max(Test);   % 每一列的最大值
MEAN = mean(Test);  % 每一列的均值
MEDIAN = median(Test);  %每一列的中位数
SKEWNESS = skewness(Test); %每一列的偏度
KURTOSIS = kurtosis(Test);  %每一列的峰度
STD = std(Test);  % 每一列的标准差
RESULT = [MIN;MAX;MEAN;MEDIAN;SKEWNESS;KURTOSIS;STD]  %将这些统计量放到一个矩阵中表示

 excel方法更好：

选中数据（包括中文如引体向上），点击上方数据，点击右边数据分析，描述统计（勾上标志位于第一行）

SPSS最好（附基础操作步骤）：

1.左上角点击文件，导入原始excel

点击上面分析，描述统计，描述（选中该选的，调调就得图）

2.看图分析：点击上面图形，旧对话框，散点图/点图，点击矩阵散点图，变量全选，生成。

各列之间相关系数：

R = corrcoef(Test)   % 返回test的相关系数矩阵
R = corrcoef(a,b)   % 返回两个随机变量a和b之间的系数

 注意：

 一定要是线性，否则结论不一定成立，例如抛物线。

2.假设性检验(正态分布图)

a：犯第一类错（原假设是对的，我们却认为它是错的）的概率

b=1-a 相信原假设的概率（一般取95%） n（样本数）-2为自由度

检验值t=r*根号下n-2/1-r^2 ，r是相关系数

结合t分布表和matlab：

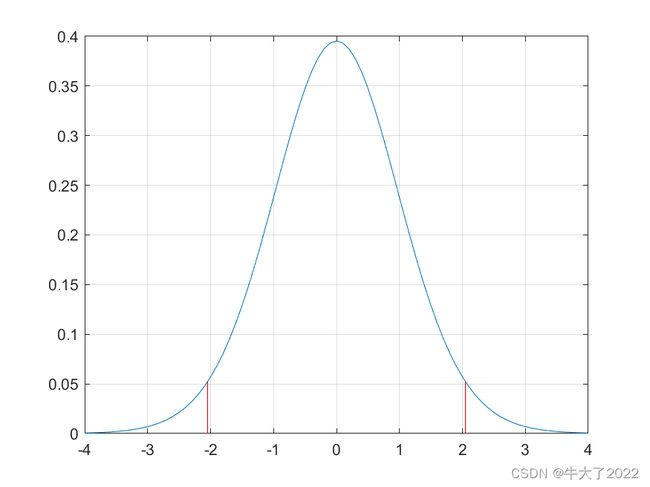
%% 假设检验部分
x = -4:0.1:4;
y = tpdf(x,28);  %求t分布的概率密度值 28是自由度  
figure(1)
plot(x,y,'-')
grid on  % 在画出的图上加上网格线
hold on  % 保留原来的图，以便继续在上面操作
% matlab可以求出临界值，函数如下
tinv(0.975,28)    %    2.0484
% 这个函数是累积密度函数cdf的反函数
plot([-2.048,-2.048],[0,tpdf(-2.048,28)],'r-')
plot([2.048,2.048],[0,tpdf(2.048,28)],'r-')

 结合最后的t分布表，可以查到自由度为28时候，置信度为0.5（双尾）对应的t为2.0484

更好用：p值判断法

%% 计算p值
x = -4:0.1:4;
y = tpdf(x,28);
figure(2)
plot(x,y,'-')
grid on 
hold on
% 画线段的方法
plot([-3.055,-3.055],[0,tpdf(-3.055,28)],'r-')
plot([3.055,3.055],[0,tpdf(3.055,28)],'r-')
disp('该检验值对应的p值为：')
disp((1-tcdf(3.055,28))*2)  %双侧检验的p值要乘以2

3.055是检验值t，最后一步是求p，这里不再细说。因为spss法最优。

p<0.01说明在99%的置信水平上拒绝原假设。

p>0.01…………相信原假设

0.05，0.10同理

 SPSS法：

把excel表里都弄过去后，原始数据分析，相关，双变量相关性，勾选皮尔逊、双尾、第三个也勾

这时会发现，数据后会带*星号，有一颗两颗的。我们规定：

P < 0.01  % 标记3颗星的位置
(P < 0.05) .* (P > 0.01)  % 标记2颗星的位置
(P < 0.1) .* (P > 0.05) % % 标记1颗星的位置

3.检验数据是否正态分布

1.正态分布JB检验（大样本n>50）

主要是根据偏度（正态分布为0）和峰度（正态分布为3），再结合jbtest函数，同时注意要循环遍历每一列。最后得p值，也是比较0.05决定是否拒绝原假设

% 正态分布的偏度和峰度
x = normrnd(2,3,100,1);   % 生成100*1的随机向量，每个元素是均值为2，标准差为3的正态分布
skewness(x)  %偏度
kurtosis(x)  %峰度
qqplot(x)
    
% 检验第一列数据是否为正态分布
[h,p] = jbtest(Test(:,1),0.05)
[h,p] = jbtest(Test(:,1),0.01)

% 用循环检验所有列的数据
n_c = size(Test,2);  % number of column 数据的列数
H = zeros(1,6);  % 初始化节省时间和消耗
P = zeros(1,6);
for i = 1:n_c
    [h,p] = jbtest(Test(:,i),0.05);
    H(i)=h;
    P(i)=p;
end
disp(H)
disp(P)

h=1拒绝原假设，h为0不能拒绝原假设。p即为p值。 

2.夏皮洛-威尔克检验（小样本 3《n《50）

用SPSS：

分析，描述统计，探索，全选后点 图，勾选含检验的正态图，最后生成正态检验图。

看h，p的方法同上。

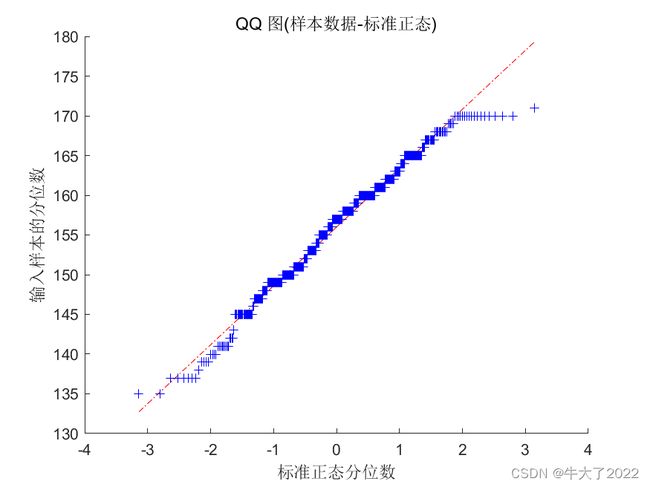
3.看图是否拟合（Q-Q图）

qqplot(Test(:,1))

 4.斯皮尔曼spearman相关系数

原理：X和Y两组数据，也有X和Y的等级（一个数所在的一列数按照从小到大排后，这个数所在的位置，若如并列第四，均取4.5）

%% 斯皮尔曼相关系数
X = [3 8 4 7 2]'  % 一定要是列向量哦，一撇'表示求转置
Y = [5 10 9 10 6]'
% 第一种计算方法
1-6*(1+0.25+0.25+1)/5/24

% 第二种计算方法
coeff = corr(X , Y , 'type' , 'Spearman')
% 等价于：
RX = [2 5 3 4 1]
RY = [1 4.5 3 4.5 2]
R = corrcoef(RX,RY)

% 计算矩阵各列的斯皮尔曼相关系数
R = corr(Test, 'type' , 'Spearman')

（Test是591*6中考体测数据）

最后假设检验，也是看p

% 大样本下的假设检验
% 计算检验值
disp(sqrt(590)*0.0301)
% 计算p值
disp((1-normcdf(0.7311))*2) % normcdf用来计算标准正态分布的累积概率密度函数

% 直接给出相关系数和p值
[R,P]=corr(Test, 'type' , 'Spearman')

附录：T分布表

单尾检验	0.05	0.025	0.01	0.005	0.0025	0.001	0.0005
双尾检验	0.1	0.05	0.02	0.01	0.005	0.002	0.001
df
1	6.3138	12.7065	31.8193	63.6551	127.3447	318.4930	636.0450
2	2.9200	4.3026	6.9646	9.9247	14.0887	22.3276	31.5989
3	2.3534	3.1824	4.5407	5.8408	7.4534	10.2145	12.9242
4	2.1319	2.7764	3.7470	4.6041	5.5976	7.1732	8.6103
5	2.0150	2.5706	3.3650	4.0322	4.7734	5.8934	6.8688
6	1.9432	2.4469	3.1426	3.7074	4.3168	5.2076	5.9589
7	1.8946	2.3646	2.9980	3.4995	4.0294	4.7852	5.4079
8	1.8595	2.3060	2.8965	3.3554	3.8325	4.5008	5.0414
9	1.8331	2.2621	2.8214	3.2498	3.6896	4.2969	4.7809
10	1.8124	2.2282	2.7638	3.1693	3.5814	4.1437	4.5869
11	1.7959	2.2010	2.7181	3.1058	3.4966	4.0247	4.4369
12	1.7823	2.1788	2.6810	3.0545	3.4284	3.9296	4.3178
13	1.7709	2.1604	2.6503	3.0123	3.3725	3.8520	4.2208
14	1.7613	2.1448	2.6245	2.9768	3.3257	3.7874	4.1404
15	1.7530	2.1314	2.6025	2.9467	3.2860	3.7328	4.0728
16	1.7459	2.1199	2.5835	2.9208	3.2520	3.6861	4.0150
17	1.7396	2.1098	2.5669	2.8983	3.2224	3.6458	3.9651
18	1.7341	2.1009	2.5524	2.8784	3.1966	3.6105	3.9216
19	1.7291	2.0930	2.5395	2.8609	3.1737	3.5794	3.8834
20	1.7247	2.0860	2.5280	2.8454	3.1534	3.5518	3.8495
21	1.7207	2.0796	2.5176	2.8314	3.1352	3.5272	3.8193
22	1.7172	2.0739	2.5083	2.8188	3.1188	3.5050	3.7921
23	1.7139	2.0686	2.4998	2.8073	3.1040	3.4850	3.7676
24	1.7109	2.0639	2.4922	2.7970	3.0905	3.4668	3.7454
25	1.7081	2.0596	2.4851	2.7874	3.0782	3.4502	3.7251
26	1.7056	2.0555	2.4786	2.7787	3.0669	3.4350	3.7067
27	1.7033	2.0518	2.4727	2.7707	3.0565	3.4211	3.6896
28	1.7011	2.0484	2.4671	2.7633	3.0469	3.4082	3.6739
29	1.6991	2.0452	2.4620	2.7564	3.0380	3.3962	3.6594
30	1.6973	2.0423	2.4572	2.7500	3.0298	3.3852	3.6459
31	1.6955	2.0395	2.4528	2.7440	3.0221	3.3749	3.6334
32	1.6939	2.0369	2.4487	2.7385	3.0150	3.3653	3.6218
33	1.6924	2.0345	2.4448	2.7333	3.0082	3.3563	3.6109
34	1.6909	2.0322	2.4411	2.7284	3.0019	3.3479	3.6008
35	1.6896	2.0301	2.4377	2.7238	2.9961	3.3400	3.5912
36	1.6883	2.0281	2.4345	2.7195	2.9905	3.3326	3.5822
37	1.6871	2.0262	2.4315	2.7154	2.9853	3.3256	3.5737
38	1.6859	2.0244	2.4286	2.7115	2.9803	3.3190	3.5657
39	1.6849	2.0227	2.4258	2.7079	2.9756	3.3128	3.5581
40	1.6839	2.0211	2.4233	2.7045	2.9712	3.3069	3.5510

 40往后查看http://www.obhrm.net/index.php/T%E5%88%86%E5%B8%83%E8%A1%A8_t_distribution_table