数学实验课MATLAB实验报告一(题目+代码)
目录
- 前言
- 程序设计部分题目
-
- 1.(1)
-
- 题目
- 代码
- 1.(2)
-
- 题目
- 代码
- 1.(3)
-
- 题目
- 代码
- 2.
-
- 题目
- 代码
- 作图部分题目
-
- 3.
-
- 题目
- 代码
- 4.
-
- 题目
- 代码
- 5.
-
- 题目
- 代码
- 符号运算部分题目
-
- 6.
-
- 题目
- 代码
- 总结
前言
今天是2022年10月14日星期五,农历九月十九,多云,有点冷。闲得无聊就把前些天做的数学实验课作业敲上来了。一共有6个题。代码里的注释写得非常详细!!!
程序设计部分题目
1.(1)
题目
令 f ( x ) = x 2 2 f(x)=\dfrac{x^2}{2} f(x)=2x2,定义二元函数 g ( x 1 , x 2 ) = { m a x f ( x ) , x ∈ ( x 1 , x 2 ) m i n f ( x ) , x ∈ ( x 2 , x 1 ) g(x_1,x_2)=\begin{cases} max f(x),x\in(x_1,x_2) \\min f(x),x\in(x_2,x_1) \end{cases} g(x1,x2)={maxf(x),x∈(x1,x2)minf(x),x∈(x2,x1)求 g ( 4 , 3 ) , g ( − 1 , 3 ) g(4,3),g(-1,3) g(4,3),g(−1,3).
代码
首先我们编写一个函数脚本文件存储 f ( x ) f(x) f(x):
function ff=f(x)
ff=1/2*x.^2;
end
利用function定义函数。将它保存为文件f.m。
下面我们编写函数 g ( x 1 , x 2 ) g(x_1,x_2) g(x1,x2).有很多种方法可以求函数的极值,这里我用随机搜索法来求函数的极值。
function a=g(X);
tic%开始计时,记录程序运行时间
N=10000;%阈值
s=0;%最值重复次数
i=1;%循环变量
if (X(1)<=X(2))
while smaxy(i-1)%当前值比之前的最大值大
x=x0;%更换最大值点
s=0;%最大值重复次数置0
else s=s+1;%之前的最大值仍是最大值,则最值重复次数+1
end
end
i=i+1;%循环变量+1
end
b=num2str(max(maxy));
end
if (X(1)>X(2))
while s 将 g ( x 1 , x 2 ) g(x_1,x_2) g(x1,x2)的代码保存为g.m,与f.m放在同一文件夹下。在命令行窗口输入
g([4,3])
g([-1,3])
即可得到结果。不过,本题中的随机搜索方法有一定的缺陷。因为当 x 1 < x 2 x_1因为我懒为了容易理解,上面给出的代码是最基础的随机搜索思想的代码,本代码不作改进。
1.(2)
题目
编写matlab程序实现:从一个数组中去掉一个最大值,再去掉一个最小值,剩下的值求平均。并随机生成一个数组,验证程序.
代码
这个题非常简单咯,把数组中最大和最小的数的位置找出来,然后赋值为0。把数组的行数和列数求出来,数组求和除以(行数×列数-2)即可。
A=input('请输入一个数组:')
A(A==max(A,[],'all'))=0;
A(A==min(A,[],'all'))=0;
a=size(A);
average=sum(A,'all')/(a(1)*a(2)-2)
是这样吗?不是,上面的想法有一点错误。A(A==max(A,[],‘all’))=0;确实把最大值变成了0,但如果数组中有多个相等的数都是最大值,那么该行命令就会把所有这些数都变成0,而求平均时的除数一直都是(数组中元素的个数-2),那么就会得到错误的结果。为了修改这一错误,我们把命令改为只找出第一个最值所在的位置并赋为0即可。修改后的代码如下:
A=input('请输入一个数组:')
maxA=find(A==max(A,[],'all'),1);%找出第一个最大值出现的位置
minA=find(A==min(A,[],'all'),1);%第一个最小值的位置
A(maxA)=0;
A(minA)=0;
a=size(A);
average=sum(A,'all')/(a(1)*a(2)-2)
将代码随便保存成什么名字.m,点击运行,会出现“请输入一个数组:”的提示。此时在命令行窗口输入
rand(5)%随便几都可以,这里生成的是5×5的矩阵,矩阵元素是0~1内的随机数
即可验证程序。
1.(3)
题目
通过键盘任意输入一个数组(元素个数大于20),编写程序使得生成一个新的数组,要求每相邻的两个元素中间插入一个元素,这个元素是两个相邻元素的平均值。如:通过键盘输入数组[1 2 5],则编写程序输出[1 1.5 2 3.5 5].
代码
A=input('请输入一个向量:');
s=size(A);%输入的向量的行数和列数
a=zeros(1,2*s(1)*s(2)-1);%生成一个1×(2×行数×列数-1)的零向量
for i=1:s(1)*s(2)
a(2*i-1)=A(i);
end%将原向量A内的数字保存到新向量a的对应位置
for i=1:(s(1)*s(2)-1)
a(2*i)=(a(2*i-1)+a(2*i+1))/2;
end%计算A中两个相邻数的平均数,存到a内应该存到的位置
if s(1)~=1%如果输入的向量A是列向量
a=a';%把输出结果变成列向量
end
c=sprintf('%.2f ',a);
disp('输出结果:')
disp(c)
这个代码也是随便保存成什么名字都可以.m,然后运行,输入一个向量,回车。
2.
题目
| x x x | 3 3 3 | 5 5 5 | 1 1 1 | 7 7 7 | 4 4 4 | 9 9 9 | 0 0 0 | 2 2 2 | 12 12 12 | 8 8 8 | 15 15 15 | 11 11 11 | 19 19 19 | 13 13 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y y y | 3 3 3 | 1 1 1 | 1.46 1.46 1.46 | 1.92 1.92 1.92 | 2.38 2.38 2.38 | 2.84 2.84 2.84 | 3.3 3.3 3.3 | 3.7 3.7 3.7 | 4.2 4.2 4.2 | 4.69 4.69 4.69 | 5.1538 5.1538 5.1538 | 5.61 5.61 5.61 | 6.0769 6.0769 6.0769 | 6.5385 6.5385 6.5385 |
(1)要求 x x x按升序排列后,输出对应的 y y y值;
(2)如果 y = s i n x y=sinx y=sinx, 要求 x x x按升序排列后,输出对应的 y y y值.
代码
x=[3 5 1 7 4 9 0 2 12 8 15 11 19 13;
3 1 1.46 1.92 2.38 2.84 3.3 3.7 4.2 4.69 5.1538 5.61 6.0769 6.5385];
%x矩阵的第二行存着y值
x_s=sort(x(1,:));%排好序的x的第一行存入x_s
for i=1:14
[r,c]=find(x(1,:)==x_s(i));%找出x_s(i)在x中原本的位置,并记录行和列
y(i)=x(2,c);%y值就是x的第二行里,上面找出的列上的数
end
disp('(1)')%输出字符(1)
y
disp('(2)')
y=sin(x_s)
随便保存成什么名字.m,运行。。。
作图部分题目
3.
题目
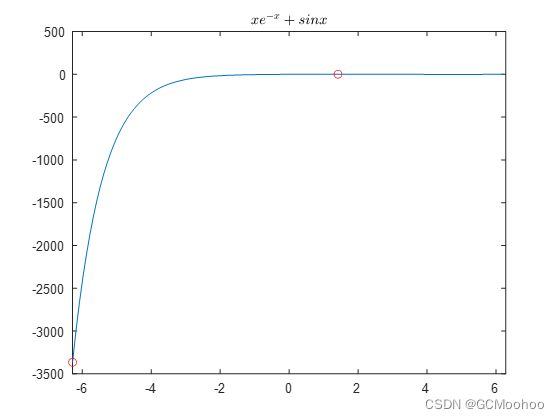
绘制函数 y = x e − x + s i n x y=xe^{-x}+sinx y=xe−x+sinx 在 [ − 2 π , 2 π ] 上 [-2π,2π]上 [−2π,2π]上的曲线,在图形上标出图名和最大、最小值点.
代码
x=-2*pi:0.1:2*pi;%x是一列向量,从-2π到2π,每隔0.1取一个值存储到x内
y=x.*exp(-1.*x)+sin(x);%计算函数值
plot(x,y)%画连线图
xlim([-2*pi,2*pi])%限定图中显示的横轴范围
title('$xe^{-x}+sinx$','Interpreter','latex')%图头
[~,lmax]=max(y)
[~,lmin]=min(y)
hold on%在上面的图中继续作图
scatter(x(lmax),y(lmax),'ro')%画散点图,标记最大值点
hold on
scatter(x(lmin),y(lmin),'ro')%标记最小值点
4.
题目
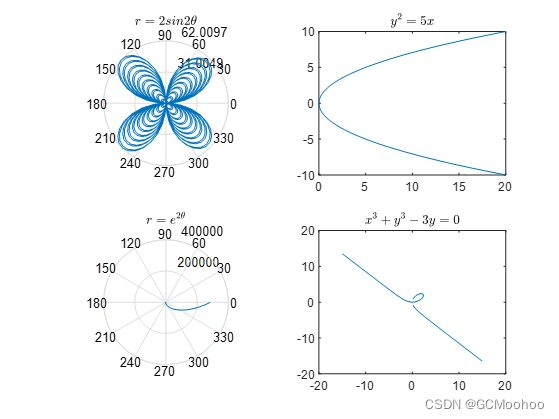
用subplot命令在4个子窗口里,分别画出四叶玫瑰线 r = 2 s i n 2 θ r=2sin2\theta r=2sin2θ,抛物线 y 2 = 5 x y^2=5x y2=5x,对数螺线 r = e 2 θ r=e^{2\theta} r=e2θ,笛卡尔叶形线 x 3 + y 3 − 3 y = 0 x^3+y^3-3y=0 x3+y3−3y=0.
代码
这个题也是不难,就是subplot比较麻烦呗,然后里面还用到了极坐标作图命令polar(x,y)。另外,笛卡尔叶形线要用参数方程来表示。四个分图中,每一个分图运用的都是第三题中的方法。给分图添加标题时使用latex来输入公式,这样显示出来比较好看。
for k = 1:4
ax(k) = subplot(2,2,k);
end
subplot(ax(1))
x=-20*pi:0.1:20*pi;
y=x.*sin(2.*x);
polar(x,y)
title('$$r=2sin2\theta$$','Interpreter','latex')%标题
subplot(ax(2))
y=-10:0.1:10;
x=1/5*y.^2;
plot(x,y)
title('$$y^2=5x$$','Interpreter','latex')
subplot(ax(3))
x=-2*pi:0.01:2*pi;
y=exp(2*x);
polar(x,y)
title('$$r=e^{2\theta}$$','Interpreter','latex')
subplot(ax(4))
a = 1.5;
t = -5:0.1:5;
x = 3*a.*t./(1+t.^3);
y = 3*a.*t.^2./(1+t.^3);
plot(x,y)
title('$$x^3+y^3-3y=0$$','Interpreter','latex')
运行结果如图:
最后一个笛卡尔叶形线,虽然是隐函数,但不推荐使用ezplot函数。一是因为MATLAB官方从R2016a起就不建议使用ezplot而推荐使用fplot与fimplicit:


二是,用ezplot画出来的图它根本就不对啊:
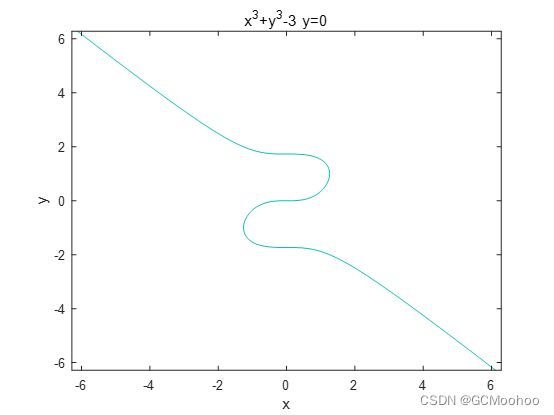
上面这个图的运行命令如下,不信可以自己去试一下:
ezplot('x^3+y^3-3*y=0')
5.
题目
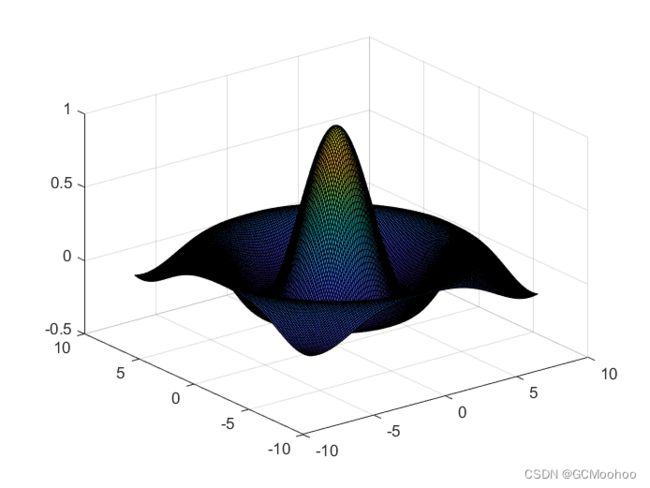
画出 z = s i n ( x 2 + y 2 ) x 2 + y 2 z=\frac{sin(\sqrt{x^2+y^2})}{\sqrt{x^2+y^2}} z=x2+y2sin(x2+y2)所表示的三维曲面, x , y x,y x,y的取值范围是 [ − 8 , 8 ] [-8,8] [−8,8].
代码
这个题目可以运用mesh或者surf命令,下面的代码用的是mesh来画一个三维网格图。
clc,clear
x=-8:0.1:8;
y=x;
for i=1:length(x)
for j=1:length(y)
s(i,j)=sqrt(x(i).^2+y(j).^2);
end
end
z=sin(s)./s;
mesh(x,y,z)
运行结果如图:
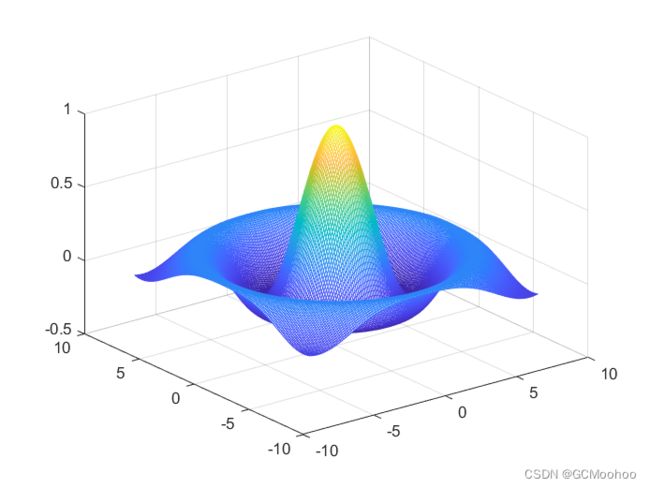
若想使用surf,只需把上面代码中的mesh改为surf。下面是运行结果:
符号运算部分题目
6.
题目
已知 f ( x ) = s i n ( 2 π x ) l n ( 4 x ) f(x)=sin(2πx)ln(4x) f(x)=sin(2πx)ln(4x),求 − d 2 f ( x ) d x 2 -\dfrac{d^2f(x)}{dx^2} −dx2d2f(x)和 ∫ 0 1 f ( x ) d x \displaystyle \int^{1}_{0}{f(x)dx} ∫01f(x)dx.
代码
syms x y%创建符号对象x和y
y=sin(2*pi*x)*log(4*x);
pretty(-1*diff(y,2))%求二阶导×(-1)并美化输出
pretty(int(y,1,2))%求1到2上的定积分,美化输出
这里使用MATLAB自带的pretty函数来使输出结果更好看。也可以使用symdisp函数来使输出结果更更美观。该函数是网友自己编写的函数,站内也有资源,请自行搜索下载。
总结
这些个题目都是非常基础的MATLAB程序设计,但是对于小(本)白(人)来说,还是要费一些时间的。而且我又有些强迫症,必须要把输出结果做的很漂亮才会满意,所以一点点地修改了很久……短时间内除了考试应该不会用到MATLAB了吧,敲上来复习一遍就当是做个阶段性总结了。