旅行商问题
题目:
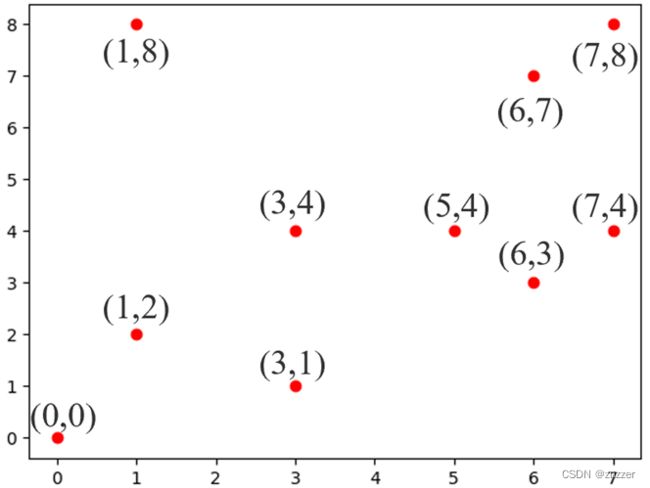
假设一个商人要去往10个城市,每个城市只拜访一次,而且最后要回到出发的城市,已知城市坐标位置如下图所示,任意两个城市之间的路径长度为直线距离,求最短旅行路径。
import matplotlib
import numpy as np
from matplotlib import pyplot as plt
def calDist(xindex, yindex):
distance = (np.sum(np.power(cities[xindex] - cities[yindex], 2))) ** 0.5
# print(distance)
# print("第{0}个点与第{1}个点之间的距离:".format("i", "j"), dis)
return distance
def tsp(v_start, v_num, v_path, dis, min_dis):
v_top = v_path[-1] # 当前所在的顶点
out_degree = len(v_edge[v_top]) # 顶点的出度
for i in range(out_degree): # 遍历与顶点v_top相连的所有边
v_start_i = v_v[v_top][i]
if v_start_i == v_start:
if v_num == len(v_path) and dis + v_edge[v_top][i] < min_dis[0]:
min_dis[0] = dis + v_edge[v_top][i]
new_path = []
for item in v_path:
new_path.append(vertex[item])
new_path.append(vertex[v_start_i])
print("new distance:", min_dis[0], "new path:", new_path)
continue
if v_start_i in v_path:
continue
v_path.append(v_v[v_top][i])
tsp(v_start, v_num, v_path, dis + v_edge[v_top][i], min_dis)
v_path.pop()
return None
if __name__ == '__main__':
cities = np.array([
[0, 0],
[1, 2],
[1, 8],
[3, 4],
[3, 1],
[5, 4],
[6, 3],
[6, 7],
[7, 4],
[7, 8],
])
dis = []
vertex = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'] # 存放所有顶点
for i in range(0, len(cities)):
for j in range(0, len(cities)):
if i != j:
dis_2 = calDist(i, j)
# print("第{0}个点与第{1}个点之间的距离:".format(i, j), dis_2)
dis.append(dis_2)
# print(len(dis))
# v_edge[i]用来存放与顶点vertex[i]相连边的长度
v_edge = np.array(dis).reshape(10, 9)
# print("v_edge:\n", v_edge)
# v_v用来存放与顶点vertex[i]相连的点
v_v = [[1, 2, 3, 4, 5, 6, 7, 8, 9],
[0, 2, 3, 4, 5, 6, 7, 8, 9],
[0, 1, 3, 4, 5, 6, 7, 8, 9],
[0, 1, 2, 4, 5, 6, 7, 8, 9],
[0, 1, 2, 3, 5, 6, 7, 8, 9],
[0, 1, 2, 3, 4, 6, 7, 8, 9],
[0, 1, 2, 3, 4, 5, 7, 8, 9],
[0, 1, 2, 3, 4, 5, 6, 8, 9],
[0, 1, 2, 3, 4, 5, 6, 7, 9],
[0, 1, 2, 3, 4, 5, 6, 7, 8]]
min_distance = [10000]
for i in range(len(vertex)):
tsp(v_start=i, v_num=len(vertex), v_path=[i], dis=0, min_dis=min_distance)
# 29.646120193589997
运行结果:
new distance: 42.520392243239485 new path: ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', '0']
new distance: 38.2044400810081 new path: ['0', '1', '2', '3', '4', '5', '6', '7', '9', '8', '0']
new distance: 37.34881936798567 new path: ['0', '1', '2', '3', '4', '5', '6', '8', '7', '9', '0']
new distance: 36.77594035237553 new path: ['0', '1', '2', '3', '4', '5', '6', '8', '9', '7', '0']
new distance: 36.012663925377296 new path: ['0', '1', '2', '3', '4', '5', '7', '9', '8', '6', '0']
new distance: 35.70758423031077 new path: ['0', '1', '2', '3', '4', '6', '8', '9', '7', '5', '0']
new distance: 33.69890871741394 new path: ['0', '1', '2', '3', '5', '6', '7', '9', '8', '4', '0']
new distance: 33.33765768825396 new path: ['0', '1', '2', '3', '5', '6', '8', '7', '9', '4', '0']
new distance: 32.82132621228641 new path: ['0', '1', '2', '3', '5', '6', '8', '9', '7', '4', '0']
new distance: 31.466737653046305 new path: ['0', '1', '2', '3', '5', '7', '9', '8', '6', '4', '0']
new distance: 31.42481178959993 new path: ['0', '1', '2', '7', '9', '6', '8', '5', '3', '4', '0']
new distance: 29.74000583838024 new path: ['0', '1', '2', '7', '9', '8', '6', '5', '3', '4', '0']
new distance: 29.646120193589997 new path: ['0', '1', '3', '2', '7', '9', '8', '6', '5', '4', '0']