YOLOv7：面向实时检测的目标检测器 | 附结构图

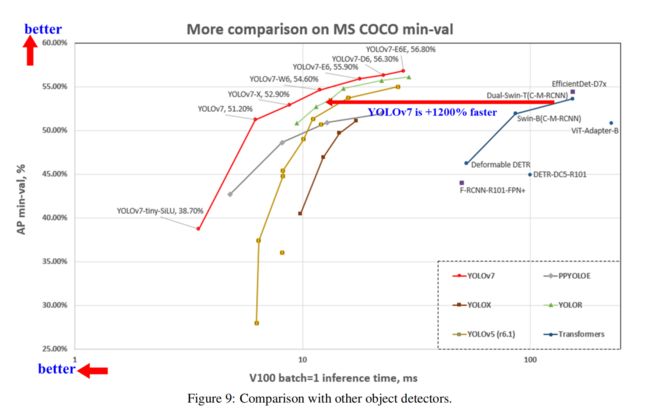
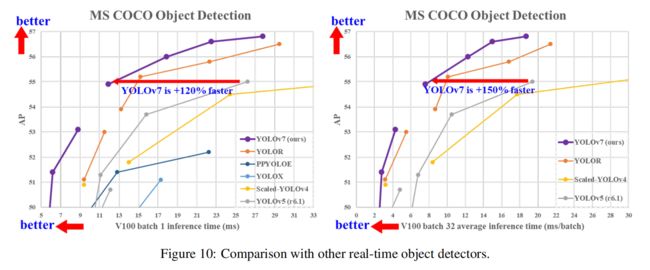
YOLOv7 在 5 FPS 到 160 FPS 范围内的速度和准确度都超过了所有已知的目标检测器，并且在 GPU V100 上 30 FPS 或更高的所有已知实时目标检测器中具有最高的准确度 56.8% AP。 YOLOv7-E6 目标检测器（56 FPS V100，55.9% AP）比基于Transformer的检测器 SWIN-L Cascade-Mask R-CNN（9.2 FPS A100，53.9% AP）的速度和准确度分别高出 509% 和 2%，并且比基于卷积的检测器 ConvNeXt-XL Cascade-Mask R-CNN (8.6 FPS A100, 55.2% AP) 速度提高 551%，准确率提高 0.7%，以及 YOLOv7 的表现还优于：YOLOR、YOLOX、Scaled-YOLOv4、YOLOv5、 DETR、Deformable DETR、DINO-5scale-R50、ViT-Adapter-B 和许多其他速度和准确度的目标检测器。 此外，只我们只在 MS COCO 数据集上从零开始训练 YOLOv7，而不使用任何其他数据集或预训练的权重。

---

模型设计

1.1 扩展的高效层聚合网络

在大多数关于设计高效架构的文献中，主要考虑因素不超过参数的数量、计算量和计算密度。 Ma 等人还从内存访问成本的特点出发，分析了输入/输出通道比、架构的分支数量以及 element-wise 操作对网络推理速度的影响。Doll 等人在执行模型缩放时还考虑了激活，即更多地考虑卷积层输出张量中的元素数量。

• 图 2（b）中 CSPVoVNet 的设计是 VoVNet 的一种变体。 CSPVoVNet 的架构除了考虑上述基本设计问题外，还分析了梯度路径，以使不同层的权重能够学习到更多样化的特征。上述梯度分析方法使推理更快、更准确。

• 图 2（c） 中的 ELAN 考虑了以下设计策略——“如何设计一个高效的网络？”。他们得出了一个结论：通过控制最短最长的梯度路径，更深的网络可以有效地学习和收敛。

在本文中，作者提出了基于 ELAN 的Extended-ELAN (E-ELAN)，其主要架构如图 2（d）所示。

无论梯度路径长度和大规模 ELAN 中计算块的堆叠数量如何，它都达到了稳定状态。如果无限堆叠更多的计算块，可能会破坏这种稳定状态，参数利用率会降低。作者提出的E-ELAN使用expand、shuffle、merge cardinality来实现在不破坏原有梯度路径的情况下不断增强网络学习能力的能力。

在架构方面，E-ELAN 只改变了计算块的架构，而过渡层的架构完全没有改变。策略是使用组卷积来扩展计算块的通道和基数。将对计算层的所有计算块应用相同的组参数和通道乘数。然后，每个计算块计算出的特征图会根据设置的组参数g被打乱成g个组，然后将它们连接在一起。此时，每组特征图的通道数将与原始架构中的通道数相同。最后，添加g组特征图来执行合并基数。 E-ELAN除了保持原有的ELAN设计架构外，还可以引导不同组的计算块学习更多样化的特征。

1.2 基于concatenate模型的模型缩放

模型缩放的主要目的是调整模型的一些属性，生成不同尺度的模型，以满足不同推理速度的需求。例如，EfficientNet的缩放模型考虑了宽度、深度和分辨率。对于Scale-yolov4，其缩放模型是调整阶段数。Doll 等人分析了卷积和群卷积对参数量和计算量的影响，并据此设计了相应的模型缩放方法。

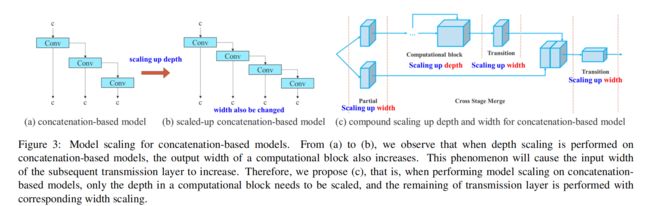
上述方法主要用于诸如PlainNet或ResNet等架构中。当这些架构在执行放大或缩小过程时，每一层的in-degree和out-degree都不会发生变化，因此可以独立分析每个缩放因子对参数量和计算量的影响。然而，如果这些方法应用于基于concatenate的架构时会发现当扩大或缩小执行深度，基于concatenate的转换层计算块将减少或增加，如图3（a）和（b）所示

从上述现象可以推断，对于基于concatenate的模型不能单独分析不同的缩放因子，而必须一起考虑。 以scaling-up depth为例，这样的动作会导致transition layer的输入通道和输出通道的比例发生变化，这可能会导致模型的硬件使用率下降。

因此，必须为基于concatenate的模型提出相应的复合模型缩放方法。 当缩放一个计算块的深度因子时，还必须计算该块的输出通道的变化。 然后，将对过渡层进行等量变化的宽度因子缩放，结果如图3（c）所示。 本文提出的复合缩放方法可以保持模型在初始设计时的特性并保持最佳结构。

训练方法

2.1 Planned re-parameterized convolution

尽管RepConv在VGG基础上取得了优异的性能，但当将它直接应用于ResNet、DenseNet和其他架构时，它的精度将显著降低。作者使用梯度流传播路径来分析重参数化的卷积应该如何与不同的网络相结合。作者还相应地设计了计划中的重参数化的卷积。

RepConv实际上结合了3×3卷积，1×1卷积，和在一个卷积层中的id连接。通过分析RepConv与不同架构的组合及其性能，作者发现RepConv中的id连接破坏了ResNet中的残差和DenseNet中的连接，为不同的特征图提供了更多的梯度多样性。

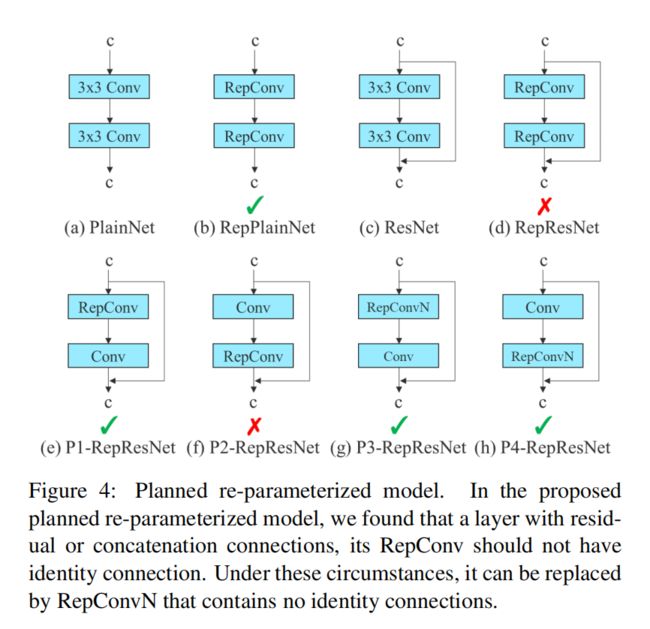
基于上述原因，作者使用没有id连接的RepConv(RepConvN)来设计计划中的重参数化卷积的体系结构。在作者的思维中，当具有残差或连接的卷积层被重新参数化的卷积所取代时，不应该存在id连接。图4显示了在PlainNet和ResNet中使用的“Planned re-parameterized convolution”的一个示例。对于基于残差的模型和基于concatenate的模型中Planned re-parameterized convolution实验，它将在消融研究环节中提出。

2.2 标签匹配

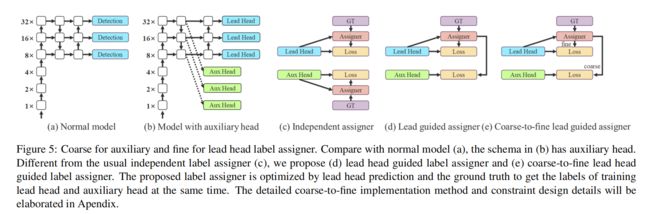
深度监督是一种常用于训练深度网络的技术。其主要概念是在网络的中间层增加额外的auxiliary Head，以及以auxiliary损失为导向的浅层网络权值。即使对于像ResNet和DenseNet这样通常收敛得很好的体系结构，深度监督仍然可以显著提高模型在许多任务上的性能。图5(a)和(b)分别显示了“没有”和“有”深度监督的目标检测器架构。在本文中，将负责最终输出的Head为lead Head，将用于辅助训练的Head称为auxiliary Head。

过去，在深度网络的训练中，标签分配通常直接指GT，并根据给定的规则生成硬标签。然而，近年来，如果以目标检测为例，研究者经常利用网络预测输出的质量和分布，然后结合GT考虑，使用一些计算和优化方法来生成可靠的软标签。例如，YOLO使用边界框回归预测和GT的IoU作为客观性的软标签。在本文中，将网络预测结果与GT一起考虑，然后将软标签分配为“label assigner”的机制。

无论auxiliary Head或lead Head的情况如何，都需要对目标目标进行深度监督培训。在软标签分配人相关技术的开发过程中，偶然发现了一个新的衍生问题，即“如何将软标签分配给 auxiliary head 和lead head？”据我们所知，相关文献迄今尚未对这一问题进行探讨。目前最常用的方法的结果如图5©所示，即将 auxiliary head 和lead head分开，然后使用它们自己的预测结果和GT来执行标签分配。本文提出的方法是一种新的标签分配方法，通过lead head预测来引导 auxiliary head 和lead head。换句话说，使用lead head预测作为指导，生成从粗到细的层次标签，分别用于 auxiliary head 和lead head的学习。所提出的2种深度监督标签分配策略分别如图5(d)和(e)所示。

1、Lead head guided label assigner

lead head引导标签分配器主要根据lead head的预测结果和GT进行计算，并通过优化过程生成软标签。这组软标签将作为 auxiliary head 和lead head的目标训练模型。这样做的原因是lead head具有相对较强的学习能力，因此由此产生的软标签应该更能代表源数据与目标之间的分布和相关性。此外，还可以将这种学习看作是一种generalized residual learning。通过让较浅的auxiliary head直接学习lead head已经学习到的信息，lead head将更能专注于学习尚未学习到的残余信息。

2、Coarse-to-fine lead head guided label assigner

从粗到细的lead head引导标签分配器也使用lead head的预测结果和GT来生成软标签。然而，在这个过程中，生成了两组不同的软标签，即粗标签和细标签，其中细标签与lead head引导标签分配器生成的软标签相同，而粗标签是通过允许更多的网格来生成的。通过放宽正样本分配过程的约束，将其视为正目标。原因是auxiliary head的学习能力不如前lead head强，为了避免丢失需要学习的信息，将重点优化auxiliary head的召回率。

至于lead head的输出，可以从高recall结果中过滤出高精度结果作为最终输出。但是，必须注意，如果粗标签的附加权重接近细标签的附加权重，则可能会在最终预测时产生不良先验。因此，为了使那些超粗的正网格影响更小，在解码器中设置了限制，使超粗的正网格不能完美地产生软标签。上述机制允许在学习过程中动态调整细标签和粗标签的重要性，使细标签的可优化上界始终高于粗标签。

2.3 其他Tricks

这些免费的训练细节将在附录中详细说明，包括：
(1) conv-bn-activation topology中的Batch normalization：这部分主要将batch normalization layer直接连接到卷积层。 这样做的目的是在推理阶段将批归一化的均值和方差整合到卷积层的偏差和权重中。

(2) 隐性知识在YOLOR中结合卷积特征图的加法和乘法方式：YOLOR中的隐式知识可以在推理阶段通过预计算简化为向量。 该向量可以与前一个或后一个卷积层的偏差和权重相结合。

(3) EMA 模型：EMA 是一种在 mean teacher 中使用的技术，在系统中使用 EMA 模型纯粹作为最终的推理模型。

实验

3.1 Baseline对比

3.2 精度对比

3.3 速度精度对比

3.4 与其他实时目标检测器的比较

---

---