《白话机器学习的数学》基础知识梳理 & 基于python的代码实现
写在前面
这本书很适合我这个机器学习小白,从数学基础开始,用自己的话凝练总结,慢慢整理。未经授权,禁止转载!如需转载,请与我联系。
第一章:开始
- 机器学习初识
机器学习的基础理论和算法并不是新出现的,长久以来,计算机能够比人类更高效地读取大量的数据、学习数据的特征并从中找出数据的模式,这样的任务也称为机器学习或者模式识别。所以当我们打算用机器学习做什么事儿的时候,首先需要的就是数据,因为机器学习就是从数据中找出特征和模式的技术。现在机器学习能做的事儿更多了,主要归功于两点:
- 具备了能够收集大量数据的环境(数字化深入我们的生活,规模大到无法想象的数据也随之产生,不仅数据量变多,且数据种类增加,获取数据的渠道扩宽,数据获取难度下降)
- 具备了能够处理大量数据的环境(计算机性能越来越高、数据处理能力增强,储存设备价格降低,可以使用GPU进行数值计算,Hadoop、Spark之类的分布式处理技术逐渐成熟)
- 机器学习的算法
机器学习非常擅长的任务有:
- 回归(regression)【简单来说回归就是在处理连续数据如时间序列数据时使用的技术,从数据中学习趋势,并且做出预测,这是一种机器学习算法】
- 分类(classification)【区分邮件是否为垃圾邮件就是简单的二分类问题,三个及三个以上的问称为多分类。】
- 聚类(clustering)【根据数据是否带有标签(正确答案)分为有监督学习(使用有标签数据进行的学习)和无监督学习(没有标签),回归和分类是有监督学习,而聚类是无监督学习】
- 数学与编程
机器学习的数学基础主要涉及概率统计、微分和线性代数,编程工具主要使用python和R
第二章:学习回归——基于广告费预测点击量
- 设置问题
尝试进行根据广告费预测点击量的任务
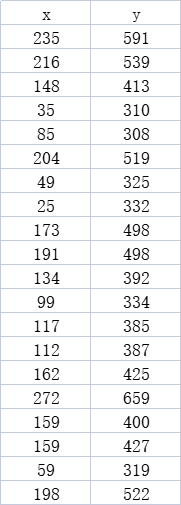
- 数据一览
x是广告费,y是点击量
- 代码一览
import numpy as np
import matplotlib.pyplot as plt
# 读入训练数据
train = np.loadtxt('click.csv', delimiter=',', dtype='int', skiprows=1)
train_x = train[:,0]
train_y = train[:,1]
# 标准化
mu = train_x.mean()
sigma = train_x.std()
def standardize(x):
return (x - mu) / sigma
train_z = standardize(train_x)
# 参数初始化
theta0 = np.random.rand()
theta1 = np.random.rand()
# 预测函数
def f(x):
return theta0 + theta1 * x
# 目标函数
def E(x, y):
return 0.5 * np.sum((y - f(x)) ** 2)
# 学习率
ETA = 1e-3
# 误差的差值
diff = 1
# 更新次数
count = 0
# 直到误差的差值小于 0.01 为止,重复参数更新
error = E(train_z, train_y)
while diff > 1e-2:
# 更新结果保存到临时变量
tmp_theta0 = theta0 - ETA * np.sum((f(train_z) - train_y))
tmp_theta1 = theta1 - ETA * np.sum((f(train_z) - train_y) * train_z)
# 更新参数
theta0 = tmp_theta0
theta1 = tmp_theta1
# 计算与上一次误差的差值
current_error = E(train_z, train_y)
diff = error - current_error
error = current_error
# 输出日志
count += 1
log = '第 {} 次 : theta0 = {:.3f}, theta1 = {:.3f}, 差值 = {:.4f}'
print(log.format(count, theta0, theta1, diff))
# 绘图确认
x = np.linspace(-3, 3, 100)
plt.plot(train_z, train_y, 'o')
plt.plot(x, f(x))
plt.show()
- 代码思路解析
- 载入相关库
-【numpy进行矢量化和数据处理,matplotlib进行绘图】 - 读入训练数据
-【读取保存有训练数据的csv文件,将两列数据分别赋予 train_x 和train_y 变量,并不是采用循环读取和计算,而是整列同时参与计算,体现了矢量化的思维,这个很重要】 - 对训练数据进行标准化
-【在训练之前,将训练数据变成平均值为0、方差为1的数据,这一步并不必须,但是做了之后,参数收敛会更快。这种做法也被称为标准化或者z-score规范化。标准化之后横轴坐标缩小,纵轴不变,所以可以直接用f(train_z) 与 train_y 进行对比】 - 利用随机数生成初始参数
-【初始参数可以任意生成,随着不断的训练,进行参数迭代更新】 - 定义预测函数(含参数和自变量)
-【这里的预测函数是一元线性函数,就是我们要用这个函数去做广告费和点击量的预测,最终得到的是包含最后更新参数的一元线性函数,如果要进行非线性预测,则可以选择不同的预测函数】 - 定义目标函数(含预测值和实际值)
-【这里的目标函数是误差和的函数,我们对每个训练数据的误差取平方之后,全部相加然后乘以1/2。使用这个目标函数,通过不断的训练和更新参数向最小值逼近,找到使E(θ)的值最小的θ,这样的问题被称为最优化问题,这种做法叫最小二乘法。如果一些任务中目标函数是表示概率,那么我们的目标就是让目标函数最大,不同的目标函数,逼近的方向也是不同的】 - 设置学习率
-【正的常数,根据学习率的大小,到达最小值的更新次数也会有变化,设置的大小比较有讲究,太大找不到最值点,太小又速度很慢。换句话说就是收敛速度会有不同,有时候还会出现无法收敛,一直发散的情况。】 - 设置误差的差值
-【这是一个初始值,新一轮误差值出现时,求两者差值,如果很小(如<0.01)则表示结果已经比较稳定,如果很大,那么还有进步空间】 - 设置更新次数
-【count从0开始,这是一个计数器】 - 直到误差的差值小于 0.01 为止,重复参数更新
-【参数的更新需要重点理解,这个更新式子是怎么得出来的,以及如何实现参数的自动更新。答案是微分和导数,只要向与导数的符号相反的方向移动x,函数就会自然而然沿着最小值的方向前进,这种方法叫最速下降法或梯度下降法。所以我们要对目标函数进行求导,目标函数中包含预测函数,预测函数中包含未知参数,所以是复合函数求偏导数,此次预测函数中包含两个未知参数,所以对应有两个参数更新式,新参数:=原参数-学习率*目标函数对某一参数求导】- 更新结果保存到临时变量
- 更新参数
- 计算与上一次误差的差值
- 输出日志
- 绘图确认
- 载入相关库
-
文章讲解顺序以及代码对应公式
-
y = θ 0 + θ 1 x y=\theta_0+\theta_1x y=θ0+θ1x, 这是我们选择用来预测的函数,一个简单的一元线性函数,拥有两个未知参数。对应的代码是:
# 预测函数
def f(x):
return theta0 + theta1 * x
- E ( θ ) = 1 2 ∑ i = 1 n ( y ( i ) − f θ ( x ( i ) ) ) 2 E\left(\theta\right)=\frac12\sum_{i=1}^n{(y^{\left(i\right)}-f_\theta\left(x^{(i)}\right))}^2 E(θ)=21∑i=1n(y(i)−fθ(x(i)))2,假设有n个训练数据,那么他们的误差和可以用这样的表达式来表示,这个表达式称为目标函数,这里的平方和乘1/2都是为了给后续的微分提供便利。对应的代码是:
# 目标函数
def E(x, y):
return 0.5 * np.sum((y - f(x)) ** 2)
- 使用最速下降法或者梯度下降法的更新表达式,一般形式( x : = x − η d d x g ( x ) x:=x-\eta\frac d{dx}g(x) x:=x−ηdxdg(x))。本题参数更新形式( θ 0 : = θ 0 − η ∂ E ∂ θ 0 \theta_0:=\theta_0-\eta\frac{\partial E}{\partial\theta_0} θ0:=θ0−η∂θ0∂E 和 θ 1 : = θ 1 − η ∂ E ∂ θ 1 \theta_1:=\theta_1-\eta\frac{\partial E}{\partial\theta_1} θ1:=θ1−η∂θ1∂E)。 ∂ E ∂ θ 0 \frac{\partial E}{\partial\theta_0} ∂θ0∂E 复合函数求导结果是= ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) \sum_{i=1}^n(f_\theta(x^{(i)})-y^{(i)}) ∑i=1n(fθ(x(i))−y(i)); ∂ E ∂ θ 1 \frac{\partial E}{\partial\theta_1} ∂θ1∂E复合函数求导结果是= ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) x ( i ) \sum_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x^{(i)} ∑i=1n(fθ(x(i))−y(i))x(i)。对应代码是:
# 更新结果保存到临时变量
tmp_theta0 = theta0 - ETA * np.sum((f(train_z) - train_y))
tmp_theta1 = theta1 - ETA * np.sum((f(train_z) - train_y) * train_z)
# 更新参数
theta0 = tmp_theta0
theta1 = tmp_theta1
- 多项式回归与代码实现(拓展)
增加函数中多项式的次数,然后再使用函数的分析方法称为多项式回归。如: f θ ( x ) = θ 0 + θ 1 x + θ 2 x 2 f_\theta(x)=\theta_0+\theta_1x+\theta_2x^2 fθ(x)=θ0+θ1x+θ2x2,在一次函数的基础上增加了一个二次项,构成二次函数,对应二次曲线,有时候能够更好的进行数据拟合,可以不断叠加次数,用更大次数的表达式,表达更加复杂的曲线,当然也需要注意过拟合问题,这个我们下面再说。先看二次函数如何进行参数更新,同样也是用目标函数分别对 θ 0 \theta_0 θ0、 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2求偏微分:
- θ 0 : = θ 0 − η ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) \theta_0:=\theta_0-\eta\sum_{i=1}^n(f_\theta(x^{(i)})-y^{(i)}) θ0:=θ0−η∑i=1n(fθ(x(i))−y(i))
- θ 1 : = θ 1 − η ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) x ( i ) \theta_1:=\theta_1-\eta\sum_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x^{(i)} θ1:=θ1−η∑i=1n(fθ(x(i))−y(i))x(i)
- θ 2 : = θ 2 − η ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) x ( i ) 2 \theta_2:=\theta_2-\eta\sum_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x^{{(i)}^2} θ2:=θ2−η∑i=1n(fθ(x(i))−y(i))x(i)2
- 代码一览
import numpy as np
import matplotlib.pyplot as plt
# 读入训练数据
train = np.loadtxt('click.csv', delimiter=',', dtype='int', skiprows=1)
train_x = train[:,0]
train_y = train[:,1]
# 标准化
mu = train_x.mean()
sigma = train_x.std()
def standardize(x):
return (x - mu) / sigma
train_z = standardize(train_x)
# 参数初始化
theta = np.random.rand(3)
# 创建训练数据的矩阵
def to_matrix(x):
return np.vstack([np.ones(x.size), x, x ** 2]).T
X = to_matrix(train_z)
# 预测函数
def f(x):
return np.dot(x, theta)
# 目标函数
def E(x, y):
return 0.5 * np.sum((y - f(x)) ** 2)
# 学习率
ETA = 1e-3
# 误差的差值
diff = 1
# 更新次数
count = 0
# 直到误差的差值小于 0.01 为止,重复参数更新
error = E(X, train_y)
while diff > 1e-2:
# 更新结果保存到临时变量
theta = theta - ETA * np.dot(f(X) - train_y, X)
# 计算与上一次误差的差值
current_error = E(X, train_y)
diff = error - current_error
error = current_error
# 输出日志
count += 1
log = '第 {} 次 : theta = {}, 差值 = {:.4f}'
print(log.format(count, theta, diff))
# 绘图确认
x = np.linspace(-3, 3, 100)
plt.plot(train_z, train_y, 'o')
plt.plot(x, f(to_matrix(x)))
plt.show()
-
代码重点解析(用向量化的思维来处理数据)
多项式代码整体结构和思路与单项式类似,这部分主要讲如何用向量化的思维来处理数据。前面我们提到将参数和训练数据都作为向量来处理,可以使计算变得简单,不过由于训练数据有很多,所以我们把一行数据当做一个训练数据,以矩阵的形式来处理会更好。在多项式回归的过程中,预测函数和更新表达式都需要用向量化来进行表达。预测函数表达式是: f θ ( x ) = θ 0 + θ 1 x + θ 2 x 2 f_\theta(x)=\theta_0+\theta_1x+\theta_2x^2 fθ(x)=θ0+θ1x+θ2x2
通用的更新表达式是: θ j : = θ j − η ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j:=\theta_j-\eta\sum_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x_j^{(i)} θj:=θj−η∑i=1n(fθ(x(i))−y(i))xj(i),其中,连加的部分除了用循环来表达之外,还可以用向量点乘来表示。
X = [ x 0 x 1 x 2 ] = [ x ( 1 ) T x ( 2 ) T x ( 3 ) T ⋮ x ( n ) T ] = [ 1 x ( 1 ) x ( 1 ) 2 1 x ( 2 ) x ( 2 ) 2 1 x ( 3 ) x ( 3 ) 2 ⋮ 1 x ( n ) x ( n ) 2 ] X=\left[x_0\;\;x_1\;\;x_2\right]=\begin{bmatrix}x^{{(1)}^T}\\x^{{(2)}^T}\\x^{{(3)}^T}\\\vdots\\x^{{(n)}^T}\end{bmatrix}=\begin{bmatrix}1&x^{(1)}&x^{{(1)}^2}\\1&x^{(2)}&x^{{(2)}^2}\\1&x^{(3)}&x^{{(3)}^2}\\&\vdots&\\1&x^{(n)}&x^{{(n)}^2}\end{bmatrix}\;\;\;\; X=[x0x1x2]=⎣⎢⎢⎢⎢⎢⎢⎡x(1)Tx(2)Tx(3)T⋮x(n)T⎦⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎡1111x(1)x(2)x(3)⋮x(n)x(1)2x(2)2x(3)2x(n)2⎦⎥⎥⎥⎥⎥⎥⎤
θ = [ θ 0 θ 1 θ 2 ] \theta=\begin{bmatrix}\theta_0\\\theta_1\\\theta_2\end{bmatrix} θ=⎣⎡θ0θ1θ2⎦⎤
预测表达式用 Xθ 来表达,对应代码是:
# 参数初始化,给定三个初始化参数,赋值给变量theta
theta = np.random.rand(3)
# 创建训练数据的矩阵
# np.vstack:按垂直方向(行顺序)堆叠数组构成一个新的数组
def to_matrix(x):
return np.vstack([np.ones(x.size), x, x ** 2]).T
X = to_matrix(train_z)
# 预测函数
def f(x):
return np.dot(x, theta)
f = [ f θ ( x ( 1 ) ) − y ( 1 ) f θ ( x ( 2 ) ) − y ( 2 ) ⋮ f θ ( x ( n ) ) − y ( n ) ] f=\begin{bmatrix}f_\theta(x^{(1)})-y^{(1)}\\f_\theta(x^{(2)})-y^{(2)}\\\vdots\\f_\theta(x^{(n)})-y^{(n)}\end{bmatrix} f=⎣⎢⎢⎢⎡fθ(x(1))−y(1)fθ(x(2))−y(2)⋮fθ(x(n))−y(n)⎦⎥⎥⎥⎤
更新表达式中求和的部分用 f T X f^TX fTX 来表达,这样就可以一次性更新所有 θ,对应代码是:
# 目标函数
def E(x, y):
return 0.5 * np.sum((y - f(x)) ** 2)
# 学习率
ETA = 1e-3
# 误差的差值
diff = 1
# 更新次数
count = 0
# 直到误差的差值小于 0.01 为止,重复参数更新
error = E(X, train_y)
while diff > 1e-2:
# 更新结果保存到临时变量
theta = theta - ETA * np.dot(f(X) - train_y, X)
- 多重回归与代码实现(拓展)
之前我们只考虑了一个变量的情况,根据广告费来预测点击量,而决定点击量的因素往往还有很多,如广告的展示位置,版面大小等,这些因素也加入考虑,用函数可以表达为: f θ ( x 1 , x 2 , x 3 ) = θ 0 + θ 1 x + θ 2 x + θ 3 x f_\theta(x_1,x_2,x_3)=\theta_0+\theta_1x+\theta_2x+\theta_3x fθ(x1,x2,x3)=θ0+θ1x+θ2x+θ3x,此时参数的求法也是类似的,分别求目标函数对 θ 0 \theta_0 θ0、 th e t a 1 \th eta_1 theta1、 θ 2 \theta_2 θ2、 θ 3 \theta_3 θ3的偏导数然后更新参数。这里有一个小步骤,我们要简化表达式的写法,将 θ \theta θ和x看做是向量。
θ = [ θ 0 θ 1 θ 2 . . . θ n ] \theta=\begin{bmatrix}\theta_0\\\theta_1\\\theta_2\\.\\.\\.\\\theta_n\end{bmatrix} θ=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡θ0θ1θ2...θn⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤ x = [ x 0 x 1 x 2 . . . x n ] ( x 0 = 1 ) x=\begin{bmatrix}x_0\\x_1\\x_2\\.\\.\\.\\x_n\end{bmatrix}\;(x_0=1) x=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡x0x1x2...xn⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤(x0=1)
则表达式可以表示为: f θ ( x ) = θ T x = θ 0 x 0 + θ 1 x 1 + ⋅ ⋅ ⋅ + θ n x n f_\theta(x)=\theta^Tx=\theta_0x_0+\theta_1x_1+\cdot\cdot\cdot+\theta_nx_n fθ(x)=θTx=θ0x0+θ1x1+⋅⋅⋅+θnxn
参数更新也是类似,为了一般化,我们考虑对第j个元素 θ j \theta_j θj偏微分的表达式:
θ j : = θ j − η ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j:=\theta_j-\eta\sum_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x_j^{(i)} θj:=θj−η∑i=1n(fθ(x(i))−y(i))xj(i),像这样包含了多个变量的回归成为多重回归。
多重回归的实现,基本可以像多项式回归一样使用矩阵,不过要注意对多重回归的变量进标准化时,要对每个参数都进行标准化,如果有变量x1,x2,x3,那就要分别使用每个变量的平均值和标准差进行标准化。
z 1 ( i ) = x 1 ( i ) − u 1 σ 1 z_1^{(i)}=\frac{x_1^{\left(i\right)}-u_1}{\sigma_1} z1(i)=σ1x1(i)−u1 ; z 2 ( i ) = x 2 ( i ) − u 2 σ 2 z_2^{(i)}=\frac{x_2^{\left(i\right)}-u_2}{\sigma_2} z2(i)=σ2x2(i)−u2 ; z 3 ( i ) = x 3 ( i ) − u 3 σ 3 z_3^{(i)}=\frac{x_3^{\left(i\right)}-u_3}{\sigma_3} z3(i)=σ3x3(i)−u3
- 随机梯度下降法与代码实现(拓展)
我们之前提到的最速下降法存在两个缺点,一是计算花费时间,二是容易陷入局部最优解。由于选用随机数作为初始值的情况较多,这样每次初始值都会变,进而陷入局部最优解的问题。随机梯度下降法就是以最速下降法为基础的,我们先来回顾一下最速下降法的参数更新表达式: θ j : = θ j − η ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j:=\theta_j-\eta\sum_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x_j^{(i)} θj:=θj−η∑i=1n(fθ(x(i))−y(i))xj(i),这个表达式使用了所有训练数据的误差,而在随机梯度下降法中会选择一个训练数据,并使用它来更新参数: θ j : = θ j − η ( f θ ( x ( k ) ) − y ( k ) ) x j ( k ) \theta_j:=\theta_j-\eta(f_\theta(x^{(k)})-y^{(k)})x_j^{(k)} θj:=θj−η(fθ(x(k))−y(k))xj(k),这个表达式中的k就是被随机选中的数据索引。最速下降法更新一次参数的时间,随机梯度下降法可以更新n次。
此外,随机梯度下降法由于训练数据是随机选择的,更新参数时使用的又是选择数据时的梯度,所以不容易陷入目标函数的局部最优解。除了随机选择1个训练数据的做法,此外还有随机选择m个训练数据来更新参数的做法。设随机选择m个训练数据的索引的集合为K,那么参数更新表达式为: θ j : = θ j − η ∑ k ∈ K ( f θ ( x ( k ) ) − y ( k ) ) x j ( k ) \theta_j:=\theta_j-\eta\sum_{k\in K}(f_\theta(x^{(k)})-y^{(k)})x_j^{(k)} θj:=θj−η∑k∈K(fθ(x(k))−y(k))xj(k), 这种做法被称为小批量梯度下降法。
import numpy as np
import matplotlib.pyplot as plt
# 读入训练数据
train = np.loadtxt('click.csv', delimiter=',', dtype='int', skiprows=1)
train_x = train[:,0]
train_y = train[:,1]
# 标准化
mu = train_x.mean()
sigma = train_x.std()
def standardize(x):
return (x - mu) / sigma
train_z = standardize(train_x)
# 参数初始化
theta = np.random.rand(3)
# 创建训练数据的矩阵
def to_matrix(x):
return np.vstack([np.ones(x.size), x, x ** 2]).T
X = to_matrix(train_z)
# 预测函数
def f(x):
return np.dot(x, theta)
# 均方误差
def MSE(x, y):
return (1 / x.shape[0]) * np.sum((y - f(x)) ** 2)
# 学习率
ETA = 1e-3
# 误差的差值
diff = 1
# 更新次数
count = 0
# 重复学习
error = MSE(X, train_y)
while diff > 1e-2:
# 使用随机梯度下降法更新参数
p = np.random.permutation(X.shape[0])
for x, y in zip(X[p,:], train_y[p]):
theta = theta - ETA * (f(x) - y) * x
# 计算与上一次误差的差值
current_error = MSE(X, train_y)
diff = error - current_error
error = current_error
# 输出日志
count += 1
log = '第 {} 次 : theta = {}, 差值 = {:.4f}'
print(log.format(count, theta, diff))
# 绘图确认
x = np.linspace(-3, 3, 100)
plt.plot(train_z, train_y, 'o')
plt.plot(x, f(to_matrix(x)))
plt.show()
- 代码重点解析(随机梯度下降法更新参数)
均方误差的表达式: 1 n ∑ i = 1 n ( y ( i ) − f θ ( x ( i ) ) ) 2 \frac1n\sum_{i=1}^n{(y^{\left(i\right)}-f_\theta\left(x^{(i)}\right))}^2 n1∑i=1n(y(i)−fθ(x(i)))2,对应代码是:
# 均方误差
def MSE(x, y):
return (1 / x.shape[0]) * np.sum((y - f(x)) ** 2)
使用随机梯度下降法更新参数的代码实现:
# 使用随机梯度下降法更新参数
p = np.random.permutation(X.shape[0])
# np.random.permutation():随机排列序列。0-X的行数,随机排列。
# x.shape是2个元组,表示x的形状,在这种情况下为(行数, 列数)。 x.shape[0]给出该元组中的第一个元素,即行数。
for x, y in zip(X[p,:], train_y[p]):
# for x, y in zip(list1,list2))用序列解包同时遍历多个序列
theta = theta - ETA * (f(x) - y) * x