NNDL 作业3：分别使用numpy和pytorch实现FNN例题

目录

过程推导 - 了解BP原理

数值计算 - 手动计算，掌握细节

代码实现 - numpy手推 + pytorch自动

对比【numpy】和【pytorch】程序，总结并陈述。

激活函数Sigmoid用PyTorch自带函数torch.sigmoid()，观察、总结并陈述。

激活函数Sigmoid改变为Relu，观察、总结并陈述。

损失函数MSE用PyTorch自带函数 t.nn.MSELoss()替代，观察、总结并陈述。

损失函数MSE改变为交叉熵，观察、总结并陈述。

改变步长，训练次数，观察、总结并陈述。

权值w1-w8初始值换为随机数，对比“指定权值”的结果，观察、总结并陈述。

权值w1-w8初始值换为0，观察、总结并陈述。

总结

参考

---

 

过程推导 - 了解BP原理

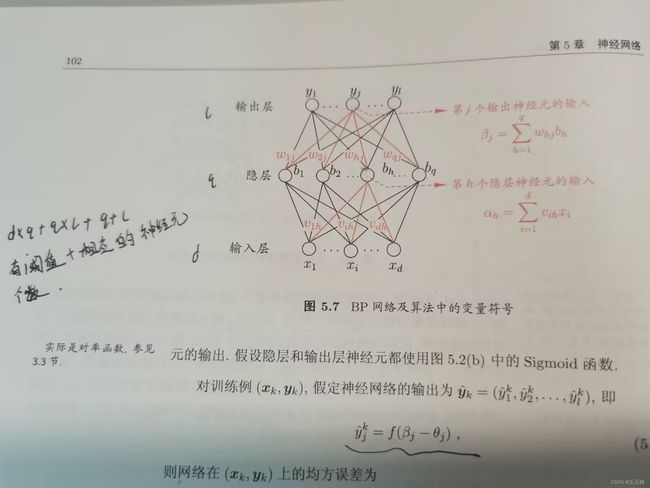
这里我是又重新翻阅了上学期学习的西瓜书，是按照西瓜书来进行推导和理解的在这里附上一张西瓜书中BP神经网络的图。

 

 这里在附上自己手写的推导：

 

数值计算 - 手动计算，掌握细节

在这里我们将这个题目中所给的参数值带入已经推好的公式中：

 

代码实现 - numpy手推 + pytorch自动

对比【numpy】和【pytorch】程序，总结并陈述。

使用numpy实现

import numpy as np


def sigmoid(z):
    a = 1 / (1 + np.exp(-z))
    return a


def forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8):
    in_h1 = w1 * x1 + w3 * x2
    out_h1 = sigmoid(in_h1)
    in_h2 = w2 * x1 + w4 * x2
    out_h2 = sigmoid(in_h2)

    in_o1 = w5 * out_h1 + w7 * out_h2
    out_o1 = sigmoid(in_o1)
    in_o2 = w6 * out_h1 + w8 * out_h2
    out_o2 = sigmoid(in_o2)

    print("正向计算：o1 ,o2")
    print(round(out_o1, 5), round(out_o2, 5))

    error = (1 / 2) * (out_o1 - y1) ** 2 + (1 / 2) * (out_o2 - y2) ** 2

    print("损失函数：均方误差")
    print(round(error, 5))

    return out_o1, out_o2, out_h1, out_h2


def back_propagate(out_o1, out_o2, out_h1, out_h2):
    # 反向传播
    d_o1 = out_o1 - y1
    d_o2 = out_o2 - y2
    # print(round(d_o1, 2), round(d_o2, 2))

    d_w5 = d_o1 * out_o1 * (1 - out_o1) * out_h1
    d_w7 = d_o1 * out_o1 * (1 - out_o1) * out_h2
    # print(round(d_w5, 2), round(d_w7, 2))
    d_w6 = d_o2 * out_o2 * (1 - out_o2) * out_h1
    d_w8 = d_o2 * out_o2 * (1 - out_o2) * out_h2
    # print(round(d_w6, 2), round(d_w8, 2))

    d_w1 = (d_w5 + d_w6) * out_h1 * (1 - out_h1) * x1
    d_w3 = (d_w5 + d_w6) * out_h1 * (1 - out_h1) * x2
    # print(round(d_w1, 2), round(d_w3, 2))

    d_w2 = (d_w7 + d_w8) * out_h2 * (1 - out_h2) * x1
    d_w4 = (d_w7 + d_w8) * out_h2 * (1 - out_h2) * x2
    # print(round(d_w2, 2), round(d_w4, 2))
    print("反向传播：误差传给每个权值")
    print(round(d_w1, 5), round(d_w2, 5), round(d_w3, 5), round(d_w4, 5), round(d_w5, 5), round(d_w6, 5),
          round(d_w7, 5), round(d_w8, 5))

    return d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8


def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
    # 步长
    step = 5
    w1 = w1 - step * d_w1
    w2 = w2 - step * d_w2
    w3 = w3 - step * d_w3
    w4 = w4 - step * d_w4
    w5 = w5 - step * d_w5
    w6 = w6 - step * d_w6
    w7 = w7 - step * d_w7
    w8 = w8 - step * d_w8
    return w1, w2, w3, w4, w5, w6, w7, w8


if __name__ == "__main__":
    w1, w2, w3, w4, w5, w6, w7, w8 = 0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8
    x1, x2 = 0.5, 0.3
    y1, y2 = 0.23, -0.07
    print("=====输入值：x1, x2；真实输出值：y1, y2=====")
    print(x1, x2, y1, y2)
    print("=====更新前的权值=====")
    print(round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
          round(w8, 2))

    for i in range(1000):
        print("=====第" + str(i) + "轮=====")
        out_o1, out_o2, out_h1, out_h2 = forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8)
        d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8 = back_propagate(out_o1, out_o2, out_h1, out_h2)
        w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)

    print("更新后的权值")
    print(round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
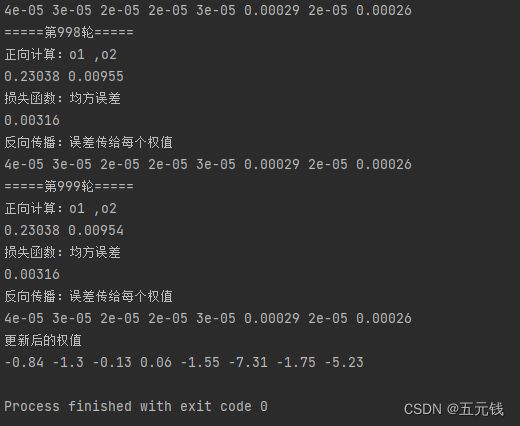
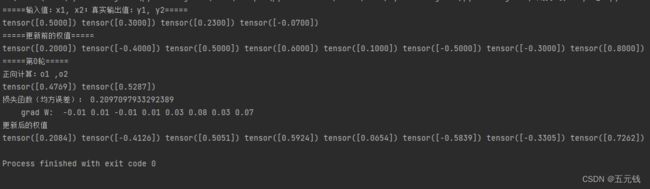
          round(w8, 2))

运行结果

使用torch实现

import torch

x1, x2 = torch.Tensor([0.5]), torch.Tensor([0.3])
y1, y2 = torch.Tensor([0.23]), torch.Tensor([-0.07])
print("=====输入值：x1, x2；真实输出值：y1, y2=====")
print(x1, x2, y1, y2)
w1, w2, w3, w4, w5, w6, w7, w8 = torch.Tensor([0.2]), torch.Tensor([-0.4]), torch.Tensor([0.5]), torch.Tensor(
    [0.6]), torch.Tensor([0.1]), torch.Tensor([-0.5]), torch.Tensor([-0.3]), torch.Tensor([0.8])  # 权重初始值
w1.requires_grad = True
w2.requires_grad = True
w3.requires_grad = True
w4.requires_grad = True
w5.requires_grad = True
w6.requires_grad = True
w7.requires_grad = True
w8.requires_grad = True


def sigmoid(z):
    a = 1 / (1 + torch.exp(-z))
    return a


def forward_propagate(x1, x2):
    in_h1 = w1 * x1 + w3 * x2
    out_h1 = sigmoid(in_h1)  # out_h1 = torch.sigmoid(in_h1)
    in_h2 = w2 * x1 + w4 * x2
    out_h2 = sigmoid(in_h2)  # out_h2 = torch.sigmoid(in_h2)

    in_o1 = w5 * out_h1 + w7 * out_h2
    out_o1 = sigmoid(in_o1)  # out_o1 = torch.sigmoid(in_o1)
    in_o2 = w6 * out_h1 + w8 * out_h2
    out_o2 = sigmoid(in_o2)  # out_o2 = torch.sigmoid(in_o2)

    print("正向计算：o1 ,o2")
    print(out_o1.data, out_o2.data)

    return out_o1, out_o2


def loss_fuction(x1, x2, y1, y2):  # 损失函数
    y1_pred, y2_pred = forward_propagate(x1, x2)  # 前向传播
    loss = (1 / 2) * (y1_pred - y1) ** 2 + (1 / 2) * (y2_pred - y2) ** 2  # 考虑 ： t.nn.MSELoss()
    print("损失函数（均方误差）：", loss.item())
    return loss


def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
    # 步长
    step = 1
    w1.data = w1.data - step * w1.grad.data
    w2.data = w2.data - step * w2.grad.data
    w3.data = w3.data - step * w3.grad.data
    w4.data = w4.data - step * w4.grad.data
    w5.data = w5.data - step * w5.grad.data
    w6.data = w6.data - step * w6.grad.data
    w7.data = w7.data - step * w7.grad.data
    w8.data = w8.data - step * w8.grad.data
    w1.grad.data.zero_()  # 注意：将w中所有梯度清零
    w2.grad.data.zero_()
    w3.grad.data.zero_()
    w4.grad.data.zero_()
    w5.grad.data.zero_()
    w6.grad.data.zero_()
    w7.grad.data.zero_()
    w8.grad.data.zero_()
    return w1, w2, w3, w4, w5, w6, w7, w8


if __name__ == "__main__":

    print("=====更新前的权值=====")
    print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)

    for i in range(1):
        print("=====第" + str(i) + "轮=====")
        L = loss_fuction(x1, x2, y1, y2)  # 前向传播，求 Loss，构建计算图
        L.backward()  # 自动求梯度，不需要人工编程实现。反向传播，求出计算图中所有梯度存入w中
        print("\tgrad W: ", round(w1.grad.item(), 2), round(w2.grad.item(), 2), round(w3.grad.item(), 2),
              round(w4.grad.item(), 2), round(w5.grad.item(), 2), round(w6.grad.item(), 2), round(w7.grad.item(), 2),
              round(w8.grad.item(), 2))
        w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)

    print("更新后的权值")
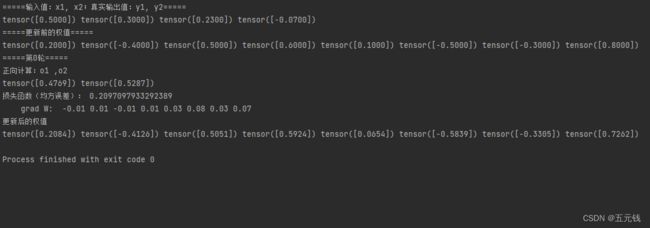
    print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)

运行结果

对比这两个程序运行结果可以发现，这两种方法求解效果相同，但是torch相较于numpy来说还是简单一些的，因为torch中已有定义好的一些函数。
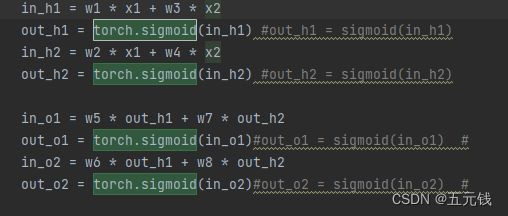
激活函数Sigmoid用PyTorch自带函数torch.sigmoid()，观察、总结并陈述。

 

 运行结果

通过对比发现使用 Sigmoid函数和使用Pytorch自带的函数torch.sigmoid()无明显差距。

 
激活函数Sigmoid改变为Relu，观察、总结并陈述。

1轮

 

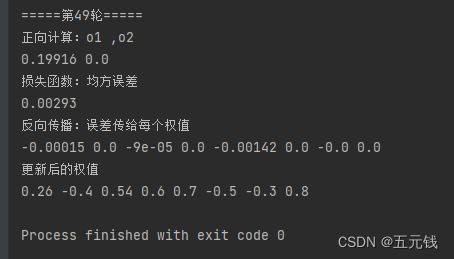
 50轮

1000轮

 （1）relu函数可使网络具有稀疏性，因为他会使一部分神经元抑制输出0，可以有效地缓解过拟合问题。

（2）relu函数计算比sigmoid函数简单，计算速度更快，计算量也比较小。

损失函数MSE用PyTorch自带函数 t.nn.MSELoss()替代，观察、总结并陈述。

 更改代码

def loss_fuction(x1, x2, y1, y2):  # 损失函数
    y1_pred, y2_pred = forward_propagate(x1, x2)  # 前向传播
    loss = torch.nn.MSELoss()  # 考虑 ： t.nn.MSELoss()
    loss1 = loss(y1_pred,y1)
    loss2 = loss(y2_pred,y2)
    loss = loss1 + loss2
    print("损失函数（MSELoss)：", loss.item())
    return loss

运行结果

 1轮

更改前

 

更改后

 

50轮

更改前

 

更改后

 

1000轮

更改前

 

更改后

 通过运行结果发现修改后两个的运行结果还是存在一些差距。
损失函数MSE改变为交叉熵，观察、总结并陈述。

 

def loss_fuction(x1, x2, y1, y2):
    y1_pred, y2_pred = forward_propagate(x1, x2)
    loss_func = torch.nn.CrossEntropyLoss() # 创建交叉熵损失函数
    y_pred = torch.stack([y1_pred, y2_pred], dim=1)
    y = torch.stack([y1, y2], dim=1)
    loss = loss_func(y_pred, y) # 计算
    print("损失函数（交叉熵损失）：", loss.item())
    return loss

运行结果

50轮

 1000轮

从这里可以看出交叉熵损失在训练1000轮后出现了负数 

改变步长，训练次数，观察、总结并陈述。

 步长为2，训练次数50：

步长为:5，训练次数50：

当训练次数一定时，步长越大，均方误差下降越快，收敛越快。 

步长为5，训练次数1：

步长为5，训练次数50： 

步长一定时，随着训练次数增加，均方误差下降速度也在逐渐降低，收敛速度也下降了。 

权值w1-w8初始值换为随机数，对比“指定权值”的结果，观察、总结并陈述。

将其换为随机数的代码

w1, w2, w3, w4, w5, w6, w7, w8 =torch.rand(1), torch.rand(1), torch.rand(1), torch.rand(1), torch.rand(1),torch.rand(1), torch.rand(1), torch.rand(1)

 训练1轮

 

 

训练50轮

训练1000轮

权重的初始化不会影响收敛的结果，均方误差的下降速度与指定权值时相比有所降低，收敛速度小于指定权值。 
权值w1-w8初始值换为0，观察、总结并陈述。

代码实现

w1, w2, w3, w4, w5, w6, w7, w8 = torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor(
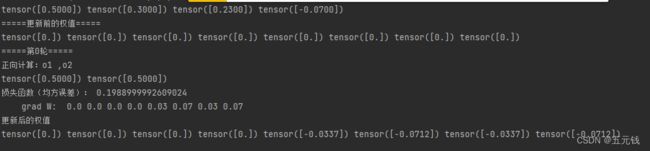
    [0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0])

 训练1轮

训练50轮

训练1000轮

权重初始值只影响收敛速度，并不会影响收敛结果。 

总结

这次作业让我在听完课后对BP算法有了一些回忆，后来在写作业时自己有重新看的学习机器学习时的西瓜书，又重新把BP算法重新推导了一遍，让自己对BP算法更加熟练，并且通过后续对激活函数和损失函数的改变调用，改变步长和训练次数并观察运行结果，让自己 对这些参数对于结果是如何影响的有了深入了解。 

参考

• 【2021-2022 春学期】人工智能-作业2：例题程序复现 numpy版
• 【2021-2022 春学期】人工智能-作业3：例题程序复现 PyTorch版