问题描述
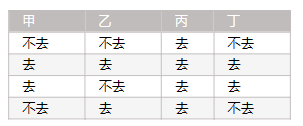
我们的问题是四个人,甲、乙、丙、丁,下面是他们之前去不去看电影的数据:
现在的问题是,如果下次可以确定:甲去、乙去、丙不去,那么丁去的概率是多少?
单节点神经网络
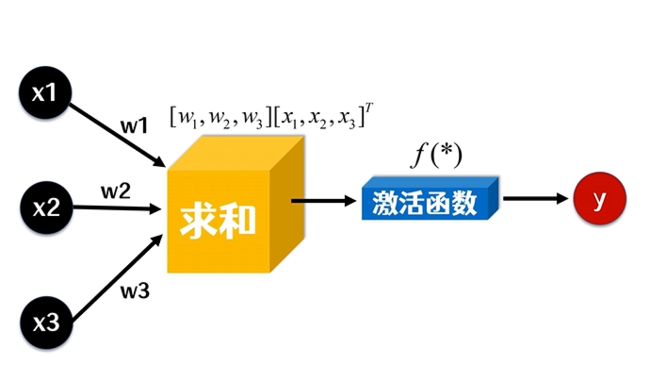
我们的模型如下:
x1、x2、x3分别表示甲、乙、丙去不去的值,去就是1,不去是0。输出y表示丁去不去的值。
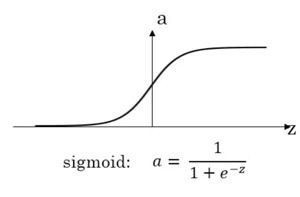
其中w1、w2、w3分别表示甲、乙、丙的权重,激活函数使用的是sigmoid,也就是:
权重进行随机,然后利用已知的值进行训练,不停调整权重,最终,把需要求解的数据输入获取结果即可。
代码实现
// 已经发生的事情,作为训练种子
let seedData = [
// 甲、乙、丙、丁去不去,0表示不去,1表示去
[0, 0, 1, 0], // 第一次
[1, 1, 1, 1], // 第二次
[1, 0, 1, 1], // 第三次
[0, 1, 1, 0] // 第四次
];
// 甲、乙、丙去不去对丁影响的权重的初始随机值: -1 ~ 1
let weights = [Math.random() * 2 - 1, Math.random() * 2 - 1, Math.random() * 2 - 1];
// 循环使用多次种子进行训练
for (let i = 0; i < 10000; i++) {
// 每次循环都利用一遍所有的种子
for (let j = 0; j < seedData.length; j++) {
// 使用sigmoid激活函数
// y = 1/(1+exp(-x))
let output = 1 / (1 + Math.exp(-1 * (seedData[j][0] * weights[0] + seedData[j][1] * weights[1] + seedData[j][2] * weights[2])));
// 对甲、乙、丙的权重分别进行调整
for (let k = 0; k < 3; k++) {
// 然后求解和实际值的差距
let error = seedData[j][3] - output;
// 每次求解完毕后,根据差距error进行调整权重weights
/**
* 在这里,调整的幅度取决于“差距”和“结果”
*
* 1.差距越大,调整的幅度也越大
* 2.对结果而言,output * (1 - output)是一个二次函数,如果结果越靠近0或1,幅度越小,反之越大
*/
let delta = error * output * (1 - output);
weights[k] += seedData[j][k] * delta;
}
}
}
let input = [1, 0, 0];
console.log(weights);
console.log(
1 / (1 + Math.exp(-1 * (input[0] * weights[0] + input[1] * weights[1] + input[2] * weights[2])))
);答疑
关于权重调整为什么要乘上输入值的理解?
weights[k] += seedData[j][k] * delta;可以看见,权重的调整最终增加的值是seedData[j][k] * delta
为什么?
delta 的值和error的正负性上保持一致,激活函数是单调递增的,如果error大于0,那么调整后激活函数的输入应该变大,可是输入可能大于0也可能小于0,怎么办?
如果增加的权重乘上输入,那么实际激活函数输入的改变就是:
seedData[j][k] * seedData[j][k] * delta = seedData[j][k]的平方 * delta也就是改变量的正负和delta保持一致,这样,目的就达到了。