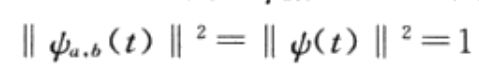小波分析,从傅里叶变换到小波变换

先说变换是什么

变换就是定义域和值域都是函数集而非数值的函数。 它仍然是一种映射，只是从函数集映射到函数集。

比如傅里叶变换和拉普拉斯变换这两种信号处理领域最先学习接触的变换方法，他们的定义域就是时间的函数，值域是频率的函数。

信号分析的主要手段就是找一个简单有效的信号变换方法，把信号里面包含的重要特征显示出来。

再说傅里叶变换有什么局限

简述FT

见过无数次的定义式

另外傅里叶级数展开的物理意义可以描述成： 一个周期性振动的量，可以看成是具有简单频率的简谐振动的叠加。

FT是域变换，时域到频域，时域看不出来的特征通常在频域会很明显。而频谱分析的本质就是对 变换到频域的信号$\hat{f}(w)$进行滤波等处理。

FT是分析平稳信号（即所有时间对应于一个频点）的有力工具。它的积分作用平滑了非平稳过程额突变部分，积分核$e^{-jwt}$的幅值在任何时候都是1。

傅里叶变换的核函数是$e^{jwt}$,即是正弦波。

FT是整体变换/全局变换。频谱$\hat{f}(w)$上每一个频点的取值都是由$f(t)$在整个时间域$(-\infty ,+\infty )$的贡献决定的，时间过程$f(t)$的每一个时间点的取值也是整个频段$(-\infty ,+\infty )$的贡献决定的。所以FT只能反映出信号的整体特征，对局部激烈震荡的细节无能为力。

FT因无法处理时变信号而裹足不前

然而

实际中的信号大多都是不平稳的时变信号（不同时间对应不同频点），我们需要知道每个时刻对应什么频率成分。

于是D.Gabor引入了STFT，并于1946年因此获诺贝尔奖。

短时傅里叶变换随着窗口在时域上滑动，可以实现时变信号的分析，看到每个时间段对应的频率成分。

STFT为了克服FT的缺点（不能处理时变信号）诞生了

但是！

STFT只有单一分辨率。因为窗口函数没有自适应功能，只能移动位置不能改变形状。

于是！

小波变换为了克服STFT的缺点（单一分辨率）诞生了

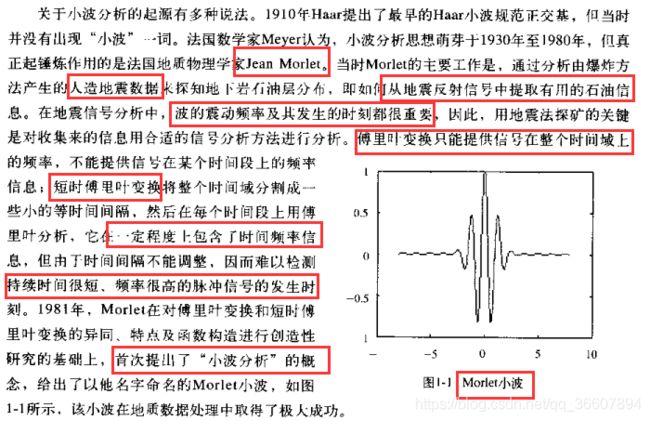
小波变换终于在1974年被法国石油信号处理工程师 J.Morlet 提出了，还构建了光滑的，在时域频域的局部性能都很好的Morlet小波。

小波变换的小波函数既可以在时域上滑动，又可以通过伸缩和平移两种操作变换窗口的形状，于是克服了STFT的单一分辨率的缺点， 开启了信号的多分辨率分析的时代。

仔细说说小波变换的真正含义

来源

有些小波无法用解析式表示，只能用计算机实现，但也得到了广泛应用 。

入门（截图来自孙延奎教授的书（小波分析及其应用））

塔式算法

小波是什么（主要讲母小波）

简单来说：长度有限（所以小），平均值为0的波形。

确切定义：满足可容许条件的平方可积函数是一个基本小波/母小波/容许小波。

• 平方可积函数是指：
  $${\int }_R|f(t){|}^{2}dt<+\infty$$
  所有平方可积函数构成的空间用$L^2(R)$表示，即$\psi (t)\in L^2(R)$.

满足${\int }_R|f(t){|}^{p}dt<+\infty$的函数空间用$L^p(R)$表示

• 小波函数的可容许条件是：
  $${\int }_R\frac{|\hat{\psi }(w){|}^2}{|w|}dw<+\infty$$

小波分析的核心：构建小波函数和多尺度分析。

小波函数的主要特质：快速衰减性和震荡性，它的子函数都是相互正交的。注意正交并不是狭义的垂直，而是说如果母小波函数通过伸缩平移变换得到N个子小波，那么不能用任意N-1个子小波去表征第N个子小波。

• 快速衰减性：时频域都有很好的局部特性。所以正弦就不是小波函数。
• 震荡性：正负交替的波动性，直流分量为0。

小波变换和傅里叶变换的区别：

1. 小波函数是快速衰减和震荡的，但FT的核函数——正弦波，是一直不变的，所以小波变换可以得到更多的信息。
2. 傅里叶变换是全局的整体的，只能单独从时域或者单独从频域表示信号；而小波分析是时频联合分析，用两个域的联合来表示信号特征。

母小波伸缩平移得到子小波

即

连续小波变换

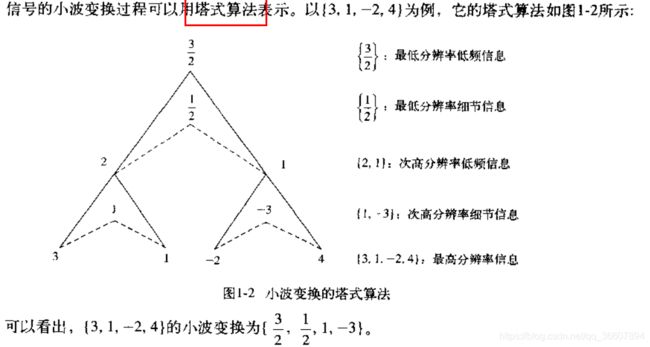
小波变换把信号拆分为多级高频信号和一级低频信号

小波去噪

去噪的理论依据：经小波分解后，信号的小波系数幅值要大于噪声的系数幅值。

查看各种小波的基本信息

>> help waveinfo
 waveinfo Information on wavelets.
    waveinfo provides information for all the wavelets
    within the toolbox.
 
    waveinfo('wname') provides information for the wavelet
    family whose short name is specified by the string 
    'wname'.
 
    Available family short names are:
    'haar'   : Haar wavelet.
    'db'     : Daubechies wavelets.
    'sym'    : Symlets.
    'coif'   : Coiflets.
    'bior'   : Biorthogonal wavelets.
    'rbio'   : Reverse biorthogonal wavelets.
    'meyr'   : Meyer wavelet.
    'dmey'   : Discrete Meyer wavelet.
    'gaus'   : Gaussian wavelets.
    'mexh'   : Mexican hat wavelet.
    'morl'   : Morlet wavelet.
    'cgau'   : Complex Gaussian wavelets.
    'cmor'   : Complex Morlet wavelets.
    'shan'   : Complex Shannon wavelets.
    'fbsp'   : Complex Frequency B-spline wavelets.
    'fk'     : Fejer-Korovkin orthogonal wavelets
 
    or user-defined short names for their own wavelet
    families (see WAVEMNGR). If the user-defined short name 
    is 'mywa' the information file must be named mywainfo.m.
    (See HAARINFO, SYMINFO ... as example of such file).
 
    waveinfo('wsys') provides information on wavelet packets.
 
    See also wavemngr.

    waveinfo 的参考页
    
>> waveinfo('haar')
 Information on Haar wavelet.
 
    Haar Wavelet
 
    General characteristics: Compactly supported 
    wavelet, the oldest and the simplest wavelet.
    
    scaling function phi = 1 on [0 1] and 0 otherwise.
    wavelet function psi = 1 on [0 0.5), = -1 on [0.5 1] and 0 otherwise.
 
    Family                  Haar
    Short name              haar
    Examples                haar is the same as db1
    Orthogonal              yes
    Biorthogonal            yes
    Compact support         yes
    DWT                     possible
    CWT                     possible
 
    Support width           1
    Filters length          2
    Regularity              haar is not continuous
    Symmetry                yes
    Number of vanishing 
    moments for psi         1
 
    Reference: I. Daubechies, 
    Ten lectures on wavelets, 
    CBMS, SIAM, 61, 1994, 194-202.

>> waveinfo('morlet')
错误使用 waveinfo (line 49)
Invalid wavelet family short name : morlet
 
>> waveinfo('morl')
 Information on Morlet wavelet.
 
    Morlet Wavelet
 
    Definition: 
    morl(x) = exp(-x^2/2) * cos(5x)
 
    Family                  Morlet
    Short name              morl
 
    Orthogonal              no
    Biorthogonal            no
    Compact support         no
    DWT                     no
    CWT                     possible
 
    Support width           infinite
    Effective support       [-4 4]
    Symmetry                yes
 
    Reference: I. Daubechies, 
    Ten lectures on wavelets, 
    CBMS, SIAM, 61, 1994, 76.

 
>> waveinfo('mexh')
 Information on Mexican Hat wavelet.
 
    Mexican Hat Wavelet
 
    Definition: second derivative of the Gaussian 
    probability density function
 
    mexh(x) = c * exp(-x^2/2) * (1-x^2)
    where c = 2/(sqrt(3)*pi^{1/4}) 
 
    Family                  Mexican hat
    Short name              mexh
 
    Orthogonal              no
    Biorthogonal            no
    Compact support         no
    DWT                     no
    CWT                     possible
 
    Support width           infinite
    Effective support       [-5 5]
    Symmetry                yes
 
    Reference: I. Daubechies, 
    Ten lectures on wavelets, 
    CBMS, SIAM, 61, 1994, 75.



>> waveinfo('db')
 Information on Daubechies wavelets.
 
    Daubechies Wavelets
 
    General characteristics: Compactly supported 
    wavelets with extremal phase and highest 
    number of vanishing moments for a given 
    support width. Associated scaling filters are
    minimum-phase filters.
 
    Family                  Daubechies
    Short name              db
    Order N                 N a positive integer from 1 to 45.
    Examples                db1 or haar, db4, db15
 
    Orthogonal              yes
    Biorthogonal            yes
    Compact support         yes
    DWT                     possible
    CWT                     possible
 
    Support width           2N-1
    Filters length          2N
    Regularity              about 0.2 N for large N
    Symmetry                far from
    Number of vanishing 
    moments for psi         N
 
    Reference: I. Daubechies, 
    Ten lectures on wavelets, 
    CBMS, SIAM, 61, 1994, 194-202.

>> waveinfo('sym')
 Information on near symmetric wavelets.
 
    Symlets Wavelets
 
    General characteristics: Compactly supported wavelets with
    least asymmetry and highest number of vanishing moments
    for a given support width.
    Associated scaling filters are near linear-phase filters.
 
    Family                  Symlets
    Short name              sym
    Order N                 N = 2, 3, ... 45 (a positive integer from 2
                                              to 45)
    Examples                sym2, sym8
 
    Orthogonal              yes
    Biorthogonal            yes
    Compact support         yes
    DWT                     possible
    CWT                     possible
 
    Support width           2N-1
    Filters length          2N
    Regularity              
    Symmetry                near from
    Number of vanishing 
    moments for psi         N
 
    Reference: I. Daubechies, 
    Ten lectures on wavelets, 
    CBMS, SIAM, 61, 1994, 198-202 and 254-256.

>> waveinfo('gauss')
错误使用 waveinfo (line 49)
Invalid wavelet family short name : gauss
 
>> waveinfo('gaus')
 Information on Gaussian wavelets.
 
    Gaussian Wavelets
 
    Definition: derivatives of the Gaussian 
    probability density function.
 
    gaus(x,n) = Cn * diff(exp(-x^2),n) where diff denotes 
    the symbolic derivative and where Cn is such that 
    the 2-norm of gaus(x,n) = 1.
 
    Family                  Gaussian
    Short name              gaus
 
    Wavelet name            'gausN'  Valid choices for N are 1,2,3,...8
 
    Orthogonal              no
    Biorthogonal            no
    Compact support         no
    DWT                     no
    CWT                     possible
 
    Support width           infinite
    Effective support       [-5 5]
    Symmetry                yes
                        n even ==> Symmetry
                        n odd  ==> Anti-Symmetry

>> 

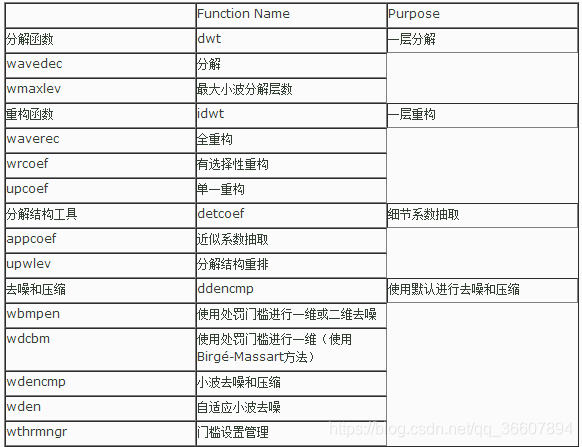
获得正交/双正交小波的分解低通，分解高通，重构低通，重构高通滤波器。

>> [lo_d,hi_d,lo_r,hi_r]=wfilters('haar')

lo_d =

    0.7071    0.7071


hi_d =

   -0.7071    0.7071


lo_r =

    0.7071    0.7071


hi_r =

    0.7071   -0.7071
    >> [f1,f2]=wfilters('haar','d')

f1 =

    0.7071    0.7071


f2 =

   -0.7071    0.7071

>> [f1,f2]=wfilters('haar','r')

f1 =

    0.7071    0.7071


f2 =

    0.7071   -0.7071

如果不是正交/双正交小波，会报错

>> [f1,f2]=wfilters('morl','d')
 
***********************************************
ERROR ...
-----------------------------------------------
 wfilters ---> The wavelet morl is not valid!
***********************************************

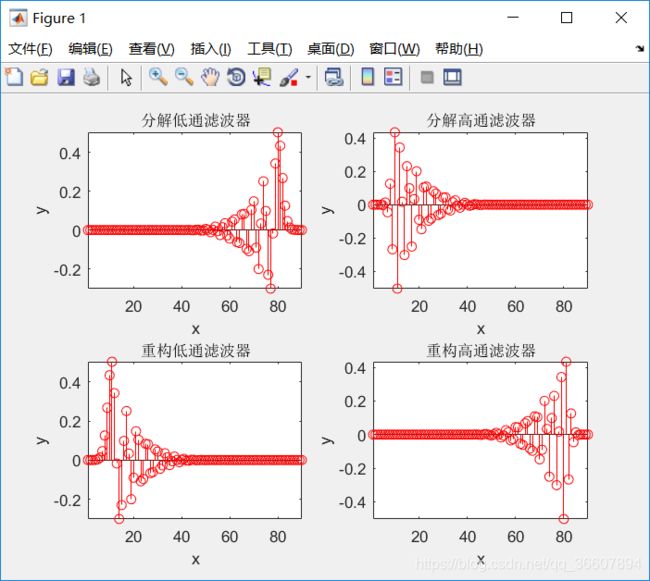
db45小波的四个滤波器

clc
clear all %清内存
clf %清除当前图形
format compact
% 'db1','db2'``````'db45','haar'是正交小波
[lo_d,hi_d,lo_r,hi_r]=wfilters('db45');%每个滤波器都有90个系数
%stem画杆状图
subplot(221);stem(lo_d,'color','r');xlim([0 95]);
title('分解低通滤波器','fontsize',10);axis tight;xlabel('x');ylabel('y');
subplot(222);stem(hi_d,'color','r');xlim([0 95]);
title('分解高通滤波器','fontsize',10);axis tight;xlabel('x');ylabel('y');
subplot(223);stem(lo_r,'color','r');xlim([0 95]);
title('重构低通滤波器','fontsize',10);axis tight;xlabel('x');ylabel('y');
subplot(224);stem(hi_r,'color','r');xlim([0 95]);
title('重构高通滤波器','fontsize',10);axis tight;xlabel('x');ylabel('y');

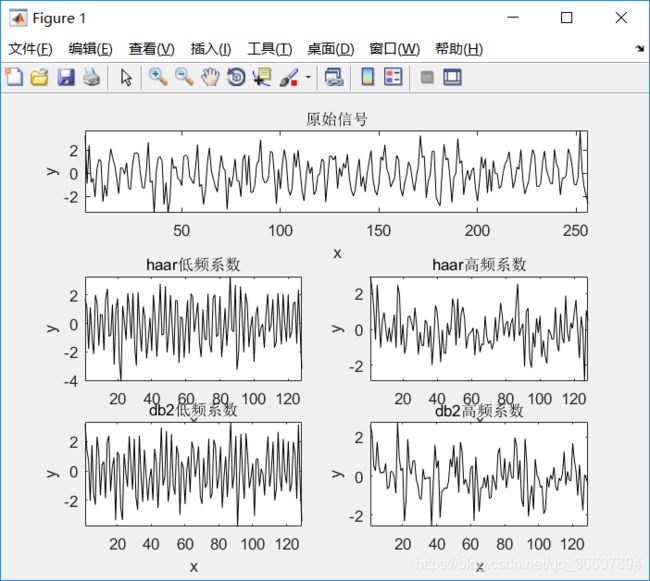
单层一维小波分解

clc
clear all
close all
clf
a=randn(1,256);
b=1.5*sin(1:256);
s=a+b;
[ca1,cd1]=dwt(s,'haar');%用haar小波为s执行单层小波分解，ca1，cd1分别是尺度系数和小波系数
subplot(311);plot(s,'k-');title('原始信号','fontsize',10);
axis tight;xlabel('x');ylabel('y');
subplot(323);plot(ca1,'k-');title('haar低频系数','fontsize',10);
axis tight;xlabel('x');ylabel('y');
subplot(324);plot(cd1,'k-');title('haar高频系数','fontsize',10);
axis tight;xlabel('x');ylabel('y');
% 计算两个分解滤波器，并用他们计算低频系数、高频系数
[lo_d,hi_d]=wfilters('haar','d');
[ca1,cd1]=dwt(s,lo_d,hi_d);
% 进行单尺度db2离散小波变换并观察最后系数的边缘效果
[ca2,cd2]=dwt(s,'db2');
subplot(325);plot(ca2,'k-');title('db2低频系数','fontsize',10);
axis tight;xlabel('x');ylabel('y');
subplot(326);plot(cd2,'k-');title('db2高频系数','fontsize',10);
axis tight;xlabel('x');ylabel('y');