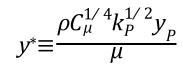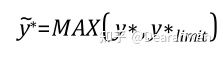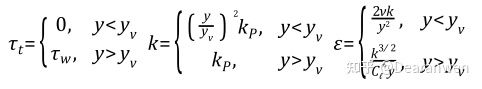四十六、Fluent壁面函数的选取依据
1. Fluent壁面函数
前面介绍了壁面函数的由来及相关的理论,这里我们介绍Fluent中壁面函数的选取依据。牢记:使用壁面函数的前提是y+>15
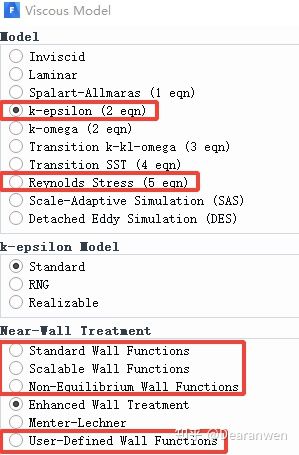
Fluent在两种湍流模型中需要选择壁面函数分别是k-e模型和Reynolds Stress雷诺应力模型,其他的湍流模型不必考虑壁面函数的问题,同时也不必考虑y+问题,我们后面会详细说明。
Fluent提供了四种壁面函数以供选择,分别是:Standard Wall Functions 标准壁面函数
Scalable Wall Functions 扩展壁面函数
Non-Equilibrium Wall Functions 非平衡壁面函数
User-Defined Wall Functions 自定义壁面函数
2. 标准壁面函数
2.1 Standard Wall Functions
标准壁面函数是由Launder and Spalding提出的,广泛应用于工业流体流动,是Fluent默认的壁面函数。但是我们计算时尽量不要使用这种壁面函数。
标准壁面函数使用典型的对数律:
其中
式中,κ= 0.4187为卡门常数;E= 9.793为经验常数;Up为紧邻壁面网格中心速度;kp为紧邻壁面网格中心湍动能;μ为动力粘度。U*和y*是Fluent中的无量纲物理量,等同于u+和y+。详情可查看四十五、壁面函数理论及y+的确定
标准壁面函数对y+要求非常严格,y+必须大于15,如果低于这个值,求解结果准确性会变得很差。其他的壁面函数对于y+的要求有所宽松,但尽量还是保证y+>15。
上述公式是对边界层内速度的近似,对于能量方程、组分方程和湍流方程同样有近似规律,这里不做介绍。
2.2 使用限制
标准壁面函数基于壁面恒剪切应力和局部平衡假设,因此当近壁流动受到很大的压力梯度的影响时(边界层分离),即流动处于非平衡状态时,预测结果可能会不准确。
其实就是因为标准壁面函数忽略了粘性底层,当粘性底层存在大压力梯度时,计算结果肯定是有问题。
3. 扩展的壁面函数
3.1 Scalable Wall Functions
顾名思义,Scalable Wall Functions在标准壁面函数的基础之上进行了扩展。当y*<11时,标准壁面函数是无法使用的,而Scalable Wall Functions可以正常使用。
Scalable Wall Functions对y*进行了一定的限制。
式中y*limit=11.25
如果y*>11.25,就取它自身的值。如果y*<11.25,就直接令y*=11.25。也就是说,y*>11.25时,Scalable Wall Functions和standard wall function功能相同。但是如果y*<11.25,那么小于11.25的网格结果相同,且都等于11.25时的规律。
举个例子,如果我们有三层网格的y*<11.25,那么这三层网格的y*直接按照等于11.25计算的,计算结果肯定是相同的。
3.2 使用限制
在y*问题上,Scalable wall functions比标准壁面函数应用范围要广,但是和标准壁面函数相同,当近壁流动受到很大的压力梯度的影响时(边界层分离),当流动处于非平衡状态时,预测结果可能会不准确。
4. 非平衡的壁面函数
4.1 Non-Equilibrium Wall Functions
由于Standard Wall Functions和Scalable wall function对于壁面压力梯度较大时都不适用,因此需要提出一种新的方式来解决这个问题。Fluent提供了Non-Equilibrium Wall Functions。
Non-Equilibrium Wall Functions基于两层假设来计算壁面剪切应力τw、湍动能k和湍动能耗散率e。而和压力梯度相关性不大的物理量如能量方程、组分方程等则和标准壁面函数保持一致。
yv为粘性底层的厚度,y为网格到壁面的距离。y处于粘性底层和粘性底层之外时,分别使用不同的公式来描述流动。
4.2 使用限制
通过这种方式,Non-Equilibrium Wall Functions能够弥补标准壁面函数的缺陷,适用于分离、撞击等复杂流动
5. 标准壁面函数 VS扩展的壁面函数
为了对比上述的内容,我们使用一个案例加以说明,案例的源文件在公众号文章chapter45中。
5.1 网格情况
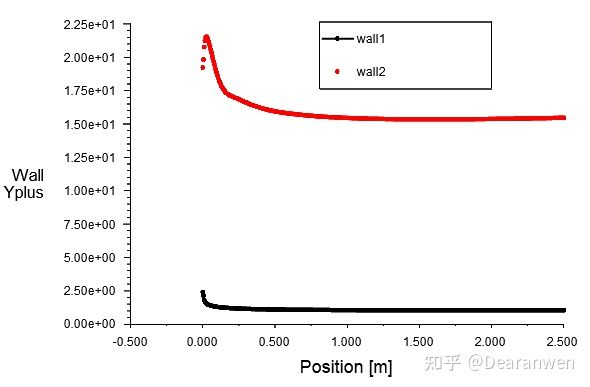
模型为二维平板,长2.5m,宽0.1m,进口流速为6m/s,物性参数保持默认。通过计算可知y+>15,第一层网格高度取2.1E-03m;y+=1时,第一层网格高度取8E-5m。分别对上下两个壁面进行不同的y+网格划分如下图
以下使用标准壁面函数进行计算。
5.2 两壁面Y+
上壁面y+基本等于1,很小;下壁面y+整体都大于15。
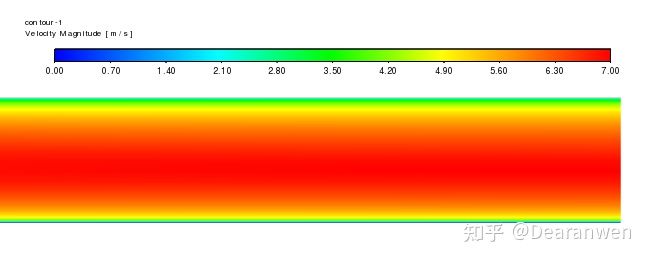
5.3 速度云图
直观上看,上下壁面的速度云图并不相同,主要还是因为标准壁面函数对y+非常敏感。通过前面的分析,我们应该知道下壁面的速度分布更加合理
通过x=1截面上的曲线图也能看出,两壁面附近速度有所区别。
5.4 扩展的壁面函数对比
标准壁面函数和扩展的壁面函数明显有所不同。两种壁面函数在y+>15处速度曲线几乎重合,而在y+很小时差距变大。Scalable wall functions在y+较小时相对更准确一些。
6. 壁面函数的使用限制
尽管基于标准壁面函数做了很多改进如Scalable Wall Functions和Non-Equilibrium Wall Functions,但是壁面函数仍然存在一些问题。
壁面函数基于对数律,要么忽略粘性底层,要么对粘性底层进行修正,对于粘性底层的求解仍然不够精确,因此对于以下问题,壁面函数并不适用:很低的雷诺数流动,如毛细现象
壁面相变问题,如壁面沸腾现象
大压力梯度导致的边界层分离现象
依靠体积力驱动的流动,如自然对流,浮力等
对于3D模型,边界层歪斜度较大也不适用壁面函数
既然壁面函数存在一些适用不了的工况,那么我们就想研究这样工况应该怎么办呢??
还记得四十五、壁面函数理论及y+的确定文章,对于边界层细节捕捉问题,其实是有两种处理方法的。第一种就是我们刚刚介绍的壁面函数的方式,第二种是我们刚开始就想到的加密网格的方式。
本来为了减少网格数量,我们想到使用壁面函数。现在壁面函数无论如何满足不了需求了,我们就只能回归老本行,通过加密网格的方式来捕获细节。
Fluent提供了两种方式用来专门捕获壁面处细节Enhanced Wall Treatment和Menter-Lechner。这部分我们下篇文章再详细讲解。
7. 壁面函数总结
1) 壁面函数只会出现在k-e模型和Reynolds Stress雷诺应力模型
2) Standard Wall Functions:适用于高雷诺数流动,要求y+>15
3) Scalable Wall Functions:也适用于高雷诺数流动,但对于y+要求比较宽松,但尽量满足y+>15。不要用Standard Wall Functions,而尽量选择Scalable Wall Functions
4) Non-Equilibrium Wall Functions:适用撞击、分离等问题,y+<15也可以使用。
5) 如果不想考虑那么多,就直接使用Scalable Wall Functions
虽然进行了壁面函数的推荐,但实际上对于k-e模型和Reynolds Stress雷诺应力模型,Fluent推荐不要使用壁面函数,而使用近壁面处理。限于篇幅,下篇文章详细讲解。
原文链接:
四十六、Fluent壁面函数的选取依据Scalable Wall Functions:也适用于高雷诺数流动,但对于y+要求比较宽松,但尽量满足y+\x26gt;15。不要用Standard Wall Functions,而尽量选择Scalable Wall Functions![]() https://mp.weixin.qq.com/s/fWnCmQYqgymU_rVbVdb0bw
https://mp.weixin.qq.com/s/fWnCmQYqgymU_rVbVdb0bw