Widar2.0：SAGE算法和SAGE算法在在无线信道参数估计中的应用

写在开头，不知道其他复现Widar2.0的人有没有碰到我这样的问题，如果我不是个例，希望这篇文章能帮助大家少走点弯路吧，大家看完问题，可以直接看后面的结论，我想到的改进方法没能解决问题。

C1 本文背景

  本科毕业论文复现Widar2.0系统，在复现过程中，信道165HT20、发包速率、天线间隔完全仿照Widar2.0论文设置，在实验采集到的数据里，有些组数据追踪效果尚可，如图1-1（a)、(b)所示，有些组数据定位结果极差，如图1-1（c）所示。图中蓝色虚线是真实人体轨迹，红色是系统追踪轨迹。

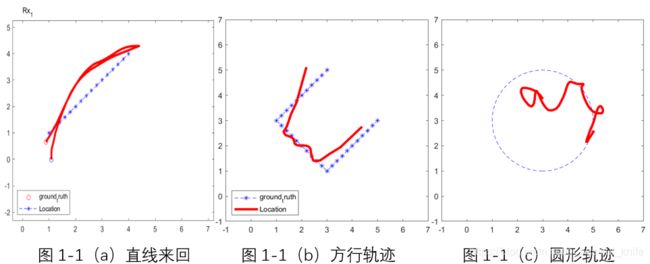
  仔细对比参数估计的图，发现定位出错时，没有一个人体反射径的估计参数是无辜的，但问题主要还是出现在ToF和AoA上。例如1-1（c）对应的那组数据，SAGE估计参数和理想人体反射多径参数对比图如图1-2所示。（于是开始寻找为何会出现参数估计错误的情况）

  更离谱的是，由于测静态数据时间长了点，为了减少跑代码的时间，本人将18000个静态数据的CSI包分成9组，每组2000个包，个别组的数据估计出的静态AoA出现了跳变，如图1-3所示。（这里就离谱就离谱）
  由于我的保研小伙伴（CSDN名：一去不复返的通信er）做的定位系统用和我同样的数据能实现人体追踪，故而排除是设备或者场地的问题。

  为了整明白为什么估计不出正确的多径参数值，首先看了Widar2.0里面的参考文献[8] Fessler J A, Hero A O. Space-alternating generalized expectation-maximization algorithm[J]. IEEE Transactions on Signal Processing, 1994, 42(10): 2664-2677。Fessler这篇论文很生艹，数学定义有点难懂。

C2 SAGE算法

  为方便描述SAGE中的一些新定义，而不是像Fessler的SAGE原论文一样全部用数学语言定义，先从EM算法开始，然后引申出SAGE的新定义。

C2.1 EM算法

EM算法：
  用于数据缺失情况下的参数估计问题。
前提：
  1）已知分布模型但模型参数待定，存在数据缺失的情况（数据缺失即有隐含参数）。
  2）M步用Jensen不等式放缩后下界f(E[X])极大化比最大似然E[f(X)]极大化容易（实际上SAGE用于信道时一般没有放缩，因为期望步骤分解后，解析形式已经很简洁了）。但为了描述后续SAGE原论文中的SAGE构造，还是不省略了。
Jensen不等式说明：针对凹函数，有E[f(X)]≥f(E[X])成立

举例：
  两枚不同的硬币，正面朝上的概率分别为a, b。随机取一枚抛5次，记录结果。重复5次。要根据五次结果估计参数a，b。后面为了和隐含参数区分，就简a和b为称显参数吧。
  在这个例子中，取到的是硬币A还是硬币B，就是隐含参数。如果隐含参数已知，问题就变成了最大似然问题。
$$\begin{array}{c}L(\theta )=L\left(x_1,\cdots ,x_n;\theta \right)={\prod }_{i=1}^{n}p\left(x_i;\theta \right),\theta \in \Theta \\ \hat{\theta }=\arg \max L(\theta )\end{array}$$
  EM算法的思想：初始化隐含参数的情况，把unknown人为赋值，求得这种情况下的两枚硬币的向上期望值；然后根据当前结果的期望值用最大似然估计的方法求a，b。然后根据a，b计算unknow最可能是哪个硬币，在用新的硬币属性去计算新的期望，然后用新的期望再去估算a，b。如此迭代至收敛。
  如果想进一步了解EM，请去知乎大佬写的EM算法详解里面看，我图都嫖的这篇文章里的。

缺陷：
  多维参数的情况下算法复杂度高，收敛慢。

C2.2 SAGE算法

  先放出原论文里的两个定义，已经人话翻译过了，建议直接对着后面举的例子理解：

定义1：定义一个索引集合S，S满足以下条件：
1）集合S非空
2）集合S是{1,…,p}的一个子集
3）集合S没有重复的元素
假设集合S中有m个元素，现用${\theta }_S$来表示由S中的元素索引的θ中的m个参数组成的新向量。用${\theta }_{\tilde{S}}$ 来表示剩下的未被索引到的参数所组成的向量。定义${\varphi }_S$表示函数或矩阵ϕ取决于S。定义Φ(θ)中θ是一个p维向量，可分为${\theta }_S$,${\theta }_{\tilde{S}}$ 两个向量，则Φ(θ)= Φ(${\theta }_S$,${\theta }_{\tilde{S}}$ )
定义2：一个概率密度为f(x;θ)的随机向量$X^S$，如果$X^S$和$Y$的联合概率密度满足：
$f(y,x;\theta )=f\left(y\mid x;{\theta }_{\tilde{S}}\right)f(x;\theta )$
那么X^S是Y关于θ_S的一个许用的隐藏数据空间。

  这两个定义是SAGE算法SA（Space–Alternating ）的基础。
  举例说明索引集和许用隐藏数据空间，它们可以看作EM里面显参数和隐含参数定义的衍生：

  在上述抛5次硬币的例子中，一共有两个显参数a，b，有5个隐参数硬币属性${\theta }_1$，${\theta }_2$，${\theta }_3$，${\theta }_4$，${\theta }_5$，隐参数一共是5个，那么定义1中m=5，如果取S={1，3}，那么索引集决定的隐藏参数集就是
${\theta }_S={\left[\begin{array}{llc}{\theta }_1& {\theta }_3& {\theta }_4\end{array}\right]}^{\prime }$,${\theta }_{\tilde{S}}={\left[\begin{array}{ll}{\theta }_2& {\theta }_5\end{array}\right]}^{\prime }$。
  不做任何映射时，${\theta }_S$的一个许用隐藏数据空间为$X_S=\left[\begin{array}{lll}{X}_1& X_3& X_4\end{array}\right]$，$X_i$的是上面最大似然函数中$x_i$对应的随机序列。我们在知道在${\theta }_{\tilde{S}}={\left[\begin{array}{ll}{\theta }_2& {\theta }_5\end{array}\right]}^{\prime }$固定时，若初始化${\theta }_S={\left[\begin{array}{llc}{\theta }_1& {\theta }_3& {\theta }_4\end{array}\right]}^{\prime }$，我们就能在许用隐藏数据空间中进行期望最大化了。减少了每次子空间中需要估计的参数，从而算法提高了收敛速度。

  Fessler原论文里面举的图像重构的索引集选取和隐藏参数集映射到许用隐藏数据空间的例子比较复杂，大伙自己去看，可以想像一下$X^S$里面是关于$X_i$的函数，不过实际上无线信道参数估计中基本不用映射,见2.3节。

  说完两个定义后，介绍以下要点和Fessler定义的流程：

SAGE算法的几个要点：

1）建立包含所有待估计参数的模型：
  这个很重要，用论文原话说就是，只有当底层通道模型包含了物理通道最相关的特征时，系统性能评估才会产生具有代表性的结果。

2）明确模型中的完整数据空间和隐藏数据空间，选定索引集
  索引集的选取会直接影响E步和M步的相对复杂度，成像问题至少有四种自然索引，这个大家自己看原论文，因为和无线信道参数估计没啥关系，知道无线信道参数估计大多是单值索引就行了。
  最大化函数一般需要通过Jensen不等式、贝叶斯定理等放缩成下界函数，个人觉得这里超难，不过还好这和无线信道参数估计没啥关系，因为无线信道参数估计的解析形式比较简单，不用去想办法放缩。

3）确定整体问题的最大化函数
  整体问题的最大化函数的构造和所建立的模型、要解决的问题息息相关，For a well-behaved objective $\Phi$, the monotonicity property ensures that the sequence $\left\{{\theta }^i\right\}$ will not diverge。这句翻译过来怪别扭的，所以这里放英语了。

4）按照索引集从最大化函数中分解期望函数和构造最大化函数。
  这部分得和C2.3结合起来看，不同的模型、问题有不同的分解方法、构造方法。原论文这部分也只说了分解，具体怎么分解是用三个例子说明的，有兴趣的自己去看。https://www.researchgate.net/publication/3315454_SpaceAlternating_Generalized_Expectation-Maximization_Algorithm

5）参数的初始化问题
  这一部分，Widar2.0里面是直接初始化为0的，很正常的做法，但后来发现可能就是这一部分导致我参数估计不对。具体阐述见C 2.3.5。

SAGE算法流程

  总而言之，SAGE算法就是通过索引集的不断变换完成参数分解，把整个最大化问题分解成索引集参数所对应的最大化问题，并通过求解对应的期望函数和最大化函数简化整体最大化问题的复杂度，提高收敛速度。注意：SAGE算法并不保证一定收敛到正确的值处，无论是SAGE还是EM，都求得是局部最优，能否收敛到正确的值，还得看索引集选的好不好、最大化函数选的好不好等。
  看完这篇1994年的论文后，理智清零，感觉自己看了个寂寞，这篇论文里图像重构的那几个SAGE构造的例子看自闭了。

C2.3 SAGE算法和SAGE算法在在无线信道参数估计中的应用

  五一假写毕设论文的空闲时间里，找了几篇SAGE用于无线信道参数估计的，个人着重推荐一篇 Fleury B H, Tschudin M, Heddergott R, et al. Channel parameter estimation in mobile radio environments using the SAGE algorithm[J]. IEEE Journal on Selected Areas in Communications, 1999, 17(3): 434-450.
  Fleury的这篇论文，因为和Widar2.0的SAGE构造有九成像，并且里面描述了和我遇到的参数估计出错问题差不多的问题，看到这篇论文时我仿佛遇上了亲爹直接泪目。
  接下来以这篇论文为例，SAGE算法用于估计是时变多径信号的时延（${\tau }_l$），入射方位角（${\varphi }_l$），入射仰角（${\beta }_l$）和复振幅（${\alpha }_l$）：

C2.3.1 模型

   假设天线阵列有m根天线，第m根天线上接收信号可以表示为：
$$h_m(t,\varphi ,\beta )=\sum _{t=1}^L{\alpha }_{\ell }\exp \left(\mathrm{j}\frac{2\pi }{\lambda }⟨r_m,e\left({\varphi }_i,{\beta }_{\ell }\right)⟩\right)\delta \left(t-{\tau }_{\ell }\right)$$
   其中，λ为波长，是$r_m$和$e({\varphi }_l,{\beta }_l)$的内积，$r_m$是一个行向量，表示第m根天线的三维坐标，$e(\varphi ,\beta )=[cos\beta cos\varphi ,cos\beta sin\varphi ,sin\beta {]}^T$。$c_m\left({\varphi }_{\ell },{\beta }_{\ell }\right)=\exp \left(\mathrm{j}\frac{2\pi }{\lambda }⟨r_m,e\left({\varphi }_{\ell },{\beta }_{\ell }\right)⟩\right)$表示由天线阵列导致的ToF引起的相移。
   定义阵列转向矩阵$c(\varphi ,\beta )={\left[c_1(\varphi ,\beta ),\dots ,c_M(\varphi ,\beta )\right]}^{\top }$。待估计参数簇${\theta }_{\ell }=\left[{\tau }_{\ell },{\varphi }_{\ell },{\vartheta }_{\ell },{\alpha }_{\ell }\right]$。那么：
$$h\left(t;{\theta }_{\ell }\right)={\left[h_1\left(t;{\theta }_{\ell }\right),\dots ,h_M\left(t;{\theta }_{\ell }\right)\right]}^{\mathrm{T}}={\alpha }_{\ell }c\left({\varphi }_{\ell },{\beta }_{\ell }\right)\delta \left(t-{\tau }_{\ell }\right)$$

   在频域内的进一步考虑噪声对阵列通道传递矩阵的破坏：（个人认为，时域不写噪声，是因为时域模型在参数估计中用不上，CSI是频域响应）

$$H(f;\theta )=\sum _{\ell =1}^L{\alpha }_{\ell }c\left({\varphi }_{\ell },{\beta }_{\ell }\right)\exp \left(-\mathrm{j}2\pi {\tau }_{\ell }f\right)+N(f)$$其中，$N(f)$是M维复高斯白噪声，$\theta =\left[{\theta }_1,\dots ,{\theta }_L\right]$是我们需要估计的参数——完全数据空间。不妨记：$S\left(f;{\theta }_{\ell }\right)={\alpha }_{\ell }c\left({\varphi }_{\ell },{\beta }_{\ell }\right)\exp \left(-\mathrm{j}2\pi {\tau }_{\ell }f\right)$，用于表示第$l$条多径对信道传递函数的贡献。（这里这样定义后，后面期望函数分解写起来方便点）

C 2.3.2 模型中的完整数据空间和隐藏数据空间

   完全数据空间是$\theta =\left[{\theta }_1,\dots ,{\theta }_L\right]$，每一个${\theta }_l$都是一个三维数组。隐藏数据空间麻烦点，按C2.3.2的步骤，得先选定单索引集，也就是每个索引集中只有一个元素（这就相当于选定一条多径嘛），然后确定选定参数${\theta }_S={\left[\begin{array}{l}{\theta }_l\end{array}\right]}^{\prime }$,可以取许用隐藏数据空间$X_S=\left[\begin{array}{l}{\theta }_l\end{array}\right]$。
   感觉这些东西的选取有点主观，需要凭经验选取，目前看过的SAGE信道估计论文中，索引集都是这么构造的，由于目前看到的文章没有说过为啥这么选，我也不知道还有没有别的构造方法。

C 2.3.3 确定整体问题的最大化函数

   这篇论文里的最大化函数为：
$$\Lambda \left({\theta }_i;X_{\ell }^{obs}\right)=2\int \Re \left\{S^{\mathrm{H}}\left(f^{\prime };{\theta }_{\ell }\right)X_{\ell }\left(f^{\prime }\right)\right\}d{f}^{\prime }-\int {\Vert S^{\mathrm{H}}\left(f^{\prime };{\theta }_{\ell }\right)\Vert }^{2}d{f}^{\prime }$$
其中，$X_{\ell }^{obs}$是每次接收装置的观测值$X_{\ell }(f)=S\left(f;{\theta }_{\ell }\right)+\sqrt{{\mu }_{\ell }}N(f)$，里面$\sum {\mu }_{\ell }=1$；$[.{]}^H$是厄密算符，当时看到这的时候，我：我在量子物理课里学过！仔细一回想：好，我已经忘了。这个最大化函数论文里没有细说选定这个最大化函数的意义和依据是什么，总之知道它选定了这样一个最大化函数，其选择原因不会影响后文的理解。
   此时${\left({\hat{\theta }}_{\ell }\right)}_{\mathrm{M}\mathrm{L}}\left(X_{\ell }^{obs}\right)\in \underset{{\theta }_l}{\mathrm{argmax}}\left\{\Lambda \left({\theta }_{\ell };X_{\ell }^{obs}\right)\right\}$。

C 2.3.4 分解后的期望函数和最大化函数

   由于所有的信号都叠加在测量信号值上，$X_l(f)$无法观测，但可以尝试获得它的估计，从观测值中除去除第l径以外的其他多径的贡献：

$Q^S\left({\theta }_S;\bar{\theta }\right)=$${\hat{X}}_{\ell }\left(f;{\hat{\theta }}^{\prime }\right)=H(f)-{\sum }_{\genfrac{}{}{0ex}{}{\ell =1}{\ell \ne \ell }}^{L}S\left(f;{\hat{\theta }}_{\ell }^{\prime }\right)$

   由于$Q^S$解析形式比较明了且不难计算，可以直接省略放缩过程，将它作为期望函数。老实说，看到这里我也惊了，在无线信道估计里面，SAGE算法好像不管最大化函数是什么，都能分解成这个期望函数，比如Widar2.0里面，${\beta }_l$取1的时候，其实本质和上式一模一样，都是第$l$条多径信号的估计值。
   M步中的最大化函数为：

${\hat{\tau }}_{\ell }^{\prime \prime }=\arg {\max }_{\tau }\left\{\left|z\left(\tau ,{\hat{\varphi }}_{\ell }^{\prime },{\hat{\beta }}_{\ell }^{\prime };{\hat{X}}_{\ell }\left(f;{\hat{\theta }}^{\prime }\right)\right)\right|\right\}$,
${\hat{\varphi }}_{\ell }^{\prime \prime }=\arg {\max }_{\varphi }\left\{\left|z\left({\hat{\tau }}_{\ell }^{\prime \prime },\varphi ,{\hat{\beta }}_{\ell }^{\prime };{\hat{X}}_{\ell }\left(f;{\hat{\theta }}^{\prime }\right)\right)\right|\right\}$,
${\hat{\beta }}_{\ell }^n=\arg {\max }_{\beta }\left\{\left|z\left({\hat{\tau }}_{\ell }^{\prime \prime },{\hat{\varphi }}_{\ell }^{\prime \prime },\beta ;{\hat{X}}_{\ell }\left(f;{\hat{\theta }}^{\prime }\right)\right)\right|\right\}$,
${\hat{\alpha }}_{\ell }^{\prime \prime }=\frac{1}{MN}z\left|\left({\hat{\tau }}_{\ell }^{\prime \prime },{\hat{\varphi }}_{\ell }^{\prime \prime },{\hat{\beta }}_{\ell }^n;{\hat{X}}_{\ell }\left(f;{\hat{\theta }}^{\prime }\right)\right)\right|$

   这一步让我看到了熟悉的Widar2.0，除了一个参数不一样，其他一模一样。

C 2.3.5 初始化

   原文中这里有这样一段话：

  文中指出，由于初始化为0导致SAGE算法的${\hat{\varphi }}_{\ell }^{\prime },{\hat{\beta }}_{\ell }^{\prime }$没有收敛到正确的值处，于是提出了用$\left({\hat{\varphi }}_{\ell }^{\prime \prime },{\hat{\beta }}_{\ell }^{\prime \prime }\right)$的二元优化替代两个一元的最大化，避免了产生错误的方位角${\hat{\varphi }}_{\ell }^{\prime },{\hat{\beta }}_{\ell }^{\prime }$估计值，尽可能收敛到正确的值处。
  感觉和我复现Widar2.0中遇到的问题太像了555。

C 3 后续打算

  1）看文献，写代码，用二元优化替代一元优化，感觉Widar2.0去遍历整个搜索空间应该不会出现这个问题啊，所以二元优化理论上不能解决这个参数估计问题，但还是得试一试。
  2）重写参数初始化，用别的方法得到一个粗略的初始值，用这个值完成初始化。
  3）不过吧，毕设写完了，这后续不一定会有后续23333。
  如果有有缘人复现Widar2.0也碰到了这个问题，可以私信我，第一版更新完了，都不知道我碰到的这个问题是不是我的个例。总之先试一试吧。
  补充：如果我理解有错的地方请帮忙指出，谢谢。
  ——以上内容2021年5月12日21点33分更新                 

2021/5/28 更新，二元优化没啥作用，可能还是环境的影响吧。另外说一点新发现，Widar2.0里面构建匹配空间时ToF有负值，所以估计出的ToF可以为负。调试后发现保留负的ToF，使得hample滤波器处理后的ToF整体变化趋势更正确，定位的精确度会比不保留负值时高。