Raptor码（一）：2007RFC5053标准编解码学习

$本文转载时请标注出处-不讲魔法讲道理CSDN$

前言：对于以下两个IETF标准
（一）2007 RFC 5053: Raptor forward error correction scheme: Scheme for object delivery
（二）2011 RaptorQ Forward Error Correction Scheme for Object Delivery, document RFC 6330
  基本所有的Raptor码相关论文都会引用的两个标准，然而目前网上没有比较系统的中文整理。本文对文献（一）进行系统学习及整理，以方便后来人更快入门。

M. Luby, A. Shokrollahi, M. Watson, and T. Stockhammer, “RFC 5053: Raptor forward error correction scheme: Scheme
for object delivery,” IETF, Tech. Rep., Oct. 2007.旨在为Raptor前向纠错码及其在数据对象的可靠交付中的应用提供参考。注意该标准是建立在GF(2)上，而6330是RaptorQ。

后续见Raptor（二）：2011 RFC6330标准学习

1. Introduction

  作为喷泉码，编码器可以根据需要从一个数据源块的源符号中即时生成任意数量的编码符号。 解码器能够从任何一组只比源符号数量稍多的编码符号中恢复源块。
  本标准构建了系统化Raptor码，使得所有的源符号都包含在生成的编码符号之中。

3. Formats and Codes

3.1 FEC Payload IDs

  FEC有效载荷ID定义为一个32位段，Source Block Number (SBN)占16bit，Encoding Symbol ID (ESI)占16bit，前者指示数据包内编码符号所涉及的源块标志；后者指示数据包内编码符号的标识。

  也就是说该标准中Raptor码需要加载32位的负载，前16位用于告知该编码符号来自于哪一个源数据块，后16位用于告知该编码符号是该源数据块的第几个编码符号。

  后续会在Sec 5 中进一步定义如何编号。

3.2 FEC Object Transmission Information (OTI)

• Mandatory FEC Encoding ID： I
• Common FEC OTI（10字节）：
  
    本FEC方案使用通用FEC对象传输信息元素：
  • Transfer Length (F)；
  • Encoding Symbol Length (T)。

  前者是一个不超过$2^{45}$的非负整数，用45bit表示；后者是一个不超过$2^{16}$的非负整数，用16bit表示。

  对符号大小限制为2^16-1限制了传输长度小于$2^{45}$。对一个源块中的符号数量的限制为$2^{13}$。对源块数量的限制为$2^{16}$。
  实际操作中，为了简单起见，传输长度被编码为一个48位的字段。

• Scheme-Specific OTI（4字节）：
  

  该FEC方案的特定FEC对象传输信息元素中包含：

  • The number of source blocks (Z)，16 bit 源块数量
  • The number of sub-blocks (N)，8 bit 子块数量
  • A symbol alignment parameter (Al)，8 bit 符号对齐参数

总结：编码后FEC对象传输信息是一个14字节（14*8bit）的字段。

  后续在Sec 5.3.1.2 中进一步定义每个段的二进制流如何生成。

4. Procedures 程序

4.1 Content Delivery Protocol Requirements 内容交付协议要求

  描述Raptor FEC方案与对象传送的内容传送协议（CDP）之间的信息交换，用于对象传送的Raptor编码器和解码器需要CDP提供以下信息：

• The transfer length of the object, F, in bytes
• A symbol alignment parameter, Al
• The symbol size, T, in bytes, which MUST be a multiple of Al
• The number of source blocks, Z
• The number of sub-blocks in each source block, N

此外Raptor编码器还需要（非CDP提供）

• the object to be encoded, F bytes

Raptor编码器为每个要发送的数据包向CDP提供以下信息：

• Source Block Number (SBN)
• Encoding Symbol ID (ESI)
• Encoding symbol(s)

4.2 Example Parameter Derivation Algorithm 参数推导算法实例

  针对4.1中的参数，给出传输参数T、Z和N的推导提供建议，该建议是基于以下输入参数：

• F the transfer length of the object, in bytes。对象的传输长度
• W a target on the sub-block size, in bytes。子块目标大小。参数W可用于生成可在解码器的有限工作内存中有效解码的编码数据。

  注意，对于一个给定的W值，实际的最大解码器内存需求取决于实现，但有可能使用仅略大于W的工作内存实现解码。

• P the maximum packet payload size, in bytes, which is assumed to be a multiple of Al。数据包最大有效载荷。
• Al the symbol alignment parameter, in bytes
• Kmax the maximum number of source 每个源块的最大源符号数量。symbols per source block.Note: Section 5.1.2 defines Kmax to be 8192.
• Kmin a minimum target on the number of symbols per source block。每个源块的符号数的最小目标
• Gmax a maximum target number of symbols per packet。每个数据包的符号数的最大目标

输出：

• G = min{ceil(P*Kmin/F), P/Al, Gmax} 代表在一个数据包中传输的最大符号数。

• T = floor(P/(Al*G))*Al ，The symbol size

  注意以上G、T是下限估计，实际中往往会增加到最接近的2的幂。在数据包最大有效载荷P/符号对齐参数AI=G的情况中，P/T是一个整数。

• Kt = ceil(F/T)，表示对象的源数据所需的符号总数。

• Z = ceil(Kt/Kmax)，The number of source blocks

• N = min{ceil(ceil(Kt/Z)*T/W), T/Al}，The number of sub-blocks

  该参数推导算法确保子符号的大小是符号对齐参数Al的倍数。 用于编码和解码的XOR操作通常是一次执行几个字节，例如，在32位处理器上一次至少执行4个字节。 因此，如果子符号大小是这个字节数的倍数，那么编码和解码的执行速度就会更快。

一般来说置AI=4 bytes，Kmin = 1024 bytes，Gmax=10。

5. Raptor FEC Code Specification 标准说明

5.1 Definitions, Symbols, and Abbreviations

5.1.1 定义

• 源块（Source block）：一个由K个源符号组成的块，为了Raptor编码的目的，这些符号被视为一起。

  信源→信源编码→信道编码→数字调制→信道，源符号是指经过信道编码后的符号流。

• 源符号（Source symbol）：编码过程中使用的最小的数据单位。 一个源块内的所有源符号都有相同的大小。
• 编码符号（Encoding sy mbol）：包含在数据包中的符号。 编码符号由源符号（Systematic code）和修复符号（Repair symbol ）组成。 从一个源块产生的修复符号与该源块的源符号具有相同的大小。
• 中间符号（Intermediate symbols）：编码过程从源符号生成的符号， 然后从中间符号生成修复符号。
• 符号：数据的一个单位。 符号的大小，以字节为单位，被称为符号大小。
• 编码符号组（Encoding symbol group）：一组一起发送的编码符号，即在同一个数据包内，其与源符号的关系可由一个编码符号ID得出。
• 编码符号ID：定义编码符号组的符号与源符号之间关系的信息。
• 编码包（Encoding packet）：包含编码符号的数据包
• 子块（Sub-block）：一个源块有时被分解成子块，每个子块都足够小，可以在工作存储器中解码。 对于一个由K个源符号组成的源块，每个子块由K个子符号组成，源块的每个符号由每个子块的一个子符号组成。
• 子符号：一个符号的一部分。 每个源符号由子符号组成，如同源块中的子块。
• 源数据包（Source packet）：包含源符号的数据包。
• 修复包（Repair packet）：包含修复符号的数据包。

5.1.2 符号

• i，j，x，h，a，b，d，v，m，X代表正整数。
• ceil(x) 对x向上取整
• floor(x) 对x向下取整
• choose(i,j) 从i个对象中不重复选择j个对象的可能取值数量。
• i%j i/j的余数
• X^Y 对于等长的比特流X和Y进行按位异或
• A 表示一个定义在GF(2)上的矩阵
• Transpose[A] 表示转置
• $A^{-1}$表示求逆
• K 单个源块中的符号数量
• C’ 表示源符号序列，C‘[0],C’[1],…,C‘[K-1]
• Kmax 表示一个源块中可包含的最大源符号数。 设为8192。
• L 表示单个源块的预编码符号的数量。
• C 表示中间符号序列，C[0],C[1],…,C[L-1]
• S 表示单个源块的LDPC符号的数量。
• H 表示单个源块的Half符号的数量。
• V0, V1 两个4-byte integers，V0[0], V0[1], …, V0[255] 和V1[0], V1[1], …, V1[255]
• Rand[X, i, m] 随机数生成器
• Deg[v] 度生成器
• LTEnc[K, C ,(d, a, b)] LT码符号生成器
• Trip[K, X] 三重生成函数
• G encoding symbol group中的符号数量
• GF(n) 有n个元素的伽罗华域
• N 一个源块中子块的数量
• T 符号大小，以字节为单位。 如果源块被划分为子块，那么T=T’*N。
• T’ 子符号的大小，以字节为单位。 如果源块没有被分割成子块，那么T’就没有意义。
• F 对象传输长度，以字节为单位
• I 子块大小，以字节为单位
• P 对于对象交付，每个数据包的有效载荷大小，以字节为单位
• Q Q=65521，即Q是小于$2^{16}$的最大素数
• Z 源块的数量，用于对象交付
• J(K) 与K相关的系统索引
• I_S 表示SxS的单位矩阵
• 0_SxH 表示SxH零矩阵

5.1.3 缩略语

• ESI Encoding Symbol ID
• LDPC Low Density Parity Check
• LT Luby Transform
• SBN Source Block Number
• SBL Source Block Length (in units of symbols)

5.2 Overview

  系统化Raptor码的主要组成部分是第5.4节中描述的基本编码器: 首先描述如何从原始源符号中得出一组中间符号的值，从而使对中间符号的了解足以重建源符号。 其次，编码器产生修复符号，它们都是一些中间符号的异或。 编码符号是源符号和修复符号的组合。 修复符号是以中间符号产生的，因此也是源符号，可以从任何足够大的编码符号集中恢复。
  5.5提供了一种有效的解码算法。实际上系统化的Raptor码编码有许多可能的解码算法。
  5.6提供用于中间符号和修复符号的构造的伪随机数。伪随机数发生器基于一组固定的512个随机数，这些随机数发送方和接收方都可用。
  从源符号中构建中间符号受 "系统指数J（K） "的制约，5.7中提供了J（K）的值，以便在从4个源符号到Kmax=8192个源符号变动时确定源块的大小。

5.3 Object Delivery

5.3.1 Source Block 构建

5.3.3.1 总体划分

  为将Raptor编码器应用于源对象，该对象可以被分解成Z >= 1个源块。编码独立作用于源块，每个源块用SBN标识，标识数从0到Z-1。每个源块划分成K个源符号，每个符号大小为T字节，每个源符号用ESI标识，标识数从0到K-1。
  每个包含K个源符号的源块可被划分为N个子块，子块足够小，可以在工作储存器中解码。每个子块被分为大小为T‘的K个字符号。

T=T’*N

  一个对象的每个源块的K值不一定相同，一个源块的每个子块的T’值也不一定相同。一个对象的所有源块的符号大小T是相同的，而源块的每个子块的符号数K也是相同的。

5.3.1.2 源块和子块的划分构建

  源块和子块的构建是根据五个输入参数F（对象的传输长度）、Al（符号对齐参数）、T（源符号大小）、Z（源块数量）和N（每个源块中的子块数量），以及函数Partition[]来确定。
  Partition[]输入整数对（J，I），输出整数(IL, IS, JL, JS)。目的是将将一个大小为I的块分割成J个近似相等的块，即长度为IL的JL个块和长度为IS的JS个块。

• IL = ceil(I/J) # 向上取整块数
• IS = floor(I/J) # 本质是商
• JL = I - IS * J # 本质是余数
• JS = J - JL # 本质是已有JL个块后，还需要多少个块

举个例子，（J，I）=（6，100），那么IL= 17，IS=16，JL=4，JS=2，此时$IL\ast JL+IS\ast JS=I$，$JS+JL=J$

  而源对象划分为源块和子块时：

• Kt = ceil(F/T)表示源对象被划分为多少个符号。

• (KL, KS, ZL, ZS) = Partition[Kt, Z]表示将Kt个符号划分为Z个源块。即对象被划分为Z = ZL + ZS连续的源块，第一个ZL源块的长度为KL×T字节，其余ZS源块的长度为KS×T字节。

    如果Kt×T>F，那么出于编码的目的，最后一个符号必须在最后填充Kt×T-F的零字节。

• (TL, TS, NL, NS) = Partition[T/Al, N]表示将源符号按照AI对齐后的数量，划分成N=NL+NS的连续子块，前NL子块每个由K个大小为TL×Al的连续子符号组成，其余NS子块每个由K个大小为TS×Al的连续子符号组成。

    这里说明源块和子符号块都是按照符号分的，不是将源块划分成子块，而是将符号划分成子符号块，确定T/AI=NL×TL+NS×TS。

  一个源块的第m个符号是由N个子块中每个子块的第m个子符号连接而成的。 请注意，这意味着当N>1时，一个符号不是对象的连续部分。

5.3.2 Encoding Packet构建

  每个包包含以下信息：

• Source Block Number (SBN)
• Encoding Symbol ID (ESI)，从0-(K-1)标识源块中的源符号，从K开始识别修复符号。
• encoding symbol(s)

  每个源块独立于其他源块进行编码。 每个编码包要么完全由源符号组成（源包），要么完全由修复符号组成（修复包）。

  一个数据包可以包含来自同一源块的任何数量的符号。 如果一个源数据包中的最后一个源符号包含填充字节，填充字节不需要包括在数据包中。 否则，必须包括整个符号。

  修复包中的符号ID，X是第一个修复符号的编码符号ID，随后X+1到X+G-1，其中G为数据包中的符号数量。接受包无需知道修复数据包的总数。
  与每个符号相关的是一个整数的triple（d，a，b）。在5.4.4.4中定义了一个triple generator，用于计算一个修复包中的符号相关triple： (d[0], a[0], b[0]),…, (d[G-1], a[G-1], b[G-1]) 。发送端根据修复符号triple，利用中间符号C和LT编码器LTEnc[K, C, (d[i], a[i], b[i])]，计算出要放在修复包中的ESI X的修复符号数量G。

For each i = 0, …, G-1, (d[i], a[i], b[i]) = Trip[K,X+i]

5.4 系统Raptor编码

编码的目的是从K个源符号组成的源块中生成修复符号。按照个人理解，编码过程全部包含在Enc函数的符号操作中，LDPC等生成矩阵不用于生成符号，而是用于解码符号。

5.4.1 Encoding Overview

  符号是编码和解码过程中的基本数据单位。对于每个源块（子块），所有的符号（子符号）都是相同大小的。编码和解码时对符号（子符号）进行的按位异或操作。

K个源符号：C’[0],…, C’[K-1]→L个中间符号：C[0],…, C[L-1]
编码STEP1：由K个源符号生成L(>K)的中间符号。预编码关系在L个中间符号中保持。由5.4.2描述。
编码STEP2：由L个中间符号生成LT码（符号数量不定）。由5.4.3描述。
STEP中用到的发生器均在5.4.4中描述。

5.4.2 First Encoding Step: Intermediate Symbol Generation

预编码步骤得到的中间符号由两组约束条件唯一确定：

1. 中间符号通过一组源符号triple与源符号相关。

     为了方便算法对源符号进行有效解码。K个源符号中的每一个都与一个Triple（d[i], a[i], b[i]）相关联。源符号triple使用triple发生器确定。即C’[i] = LTEnc[K, (C[0],…, C[L-1]), (d[i], a[i], b[i])], for all i, 0 <= i < K.

   Trip[K,X]
   输入：

   • K - The number of source symbols
   • X - An encoding symbol ID

   提前设置:

   • L 中间符号的数量
   • L’ 大于等于L的最小素数
   • Q=65521，小于$2^{16}$的最小素数

   输出: (d,a,b)
   A = (53591 + J(K)×997) % Q
   B = 10267×(J(K)+1) % Q
   Y = (B + X×A) % Q
   v = Rand[Y, 0, 2^^20]
   d = Deg[v]
   a = 1 + Rand[Y, 1, L’-1]
   b = Rand[Y, 2, L’]

2. 中间符号蕴含的预编码关系，如生成过程所示。

     L个中间符号之间的预编码关系是通过用前K个中间符号来表达最后的L-K个中间符号来定义:

   最后L-K个中间符号C[K],…,C[L-1]，有S个LDPC符号和H个Half符号组成，L=K+S+H。
   其中：

   • X是使X×(X-1)≥2K的最小正整数。
   • S是使S ≥ ceil(0.01*K) + X的最小正整数。
   • H是使choose(H,ceil(H/2)) >= K + S的最小正整数。
   • H’ = ceil(H/2)
   • L = K+S+H
   • C[K],…,C[K+S-1]表示S个LDPC符号，初始化为零
   • C[K+S],…,C[L-1]表示H个Half符号，初始化为零

生成过程：

1. S个LDPC符号的生成

   C[K],…,C[K+S-1]的值为以下过程结束时的值

   For i = 0,…,K-1 do
   a = 1 + (floor(i/S) % (S-1))
   b = i % S
   C[K + b] = C[K + b] ^ C[i]
   b = (b + a) % S
   C[K + b] = C[K + b] ^ C[i]
   b = (b + a) % S
   C[K + b] = C[K + b] ^ C[i]

2. H个Half符号的生成

     先定义格雷序列g[i] = i ^ (floor(i/2)) for all positive integers i，保证其中每个元素与前一个元素在对应单bit位上不同。m[k]表示g[·]的子序列，其元素的二进制表示中正好有k个非零位。m[j,k]表示序列m[k]的第j个元素，其中j=0，1，2，…。
   C[K+S],…,C[L-1]的值经过以下过程生成：

   For h = 0,…,H-1 do
     For j = 0,…,K+S-1 do
       If bit h of m[j,H’] is equal to 1 then C[h+K+S] = C[h+K+S] ^ C[j].

解码器中，中间符号C[0]、C[1]、…、C[L-1]计算举例：

G_LDPC是S×K的生成矩阵，有

Transpose[(C[0],…, C[K-1])]=G_LDPC * Transpose[(C[K], …, C[K+S-1])]

G_Half是H x (K+S)的生成矩阵

Transpose[(C[K+S], …, C[K+S+H-1])]=G_Half* Transpose[(C[0], …, C[S+K-1])]

G_LT是由LT编码器生成的编码符号的KxL生成器矩阵

Transpose[(C’[0],C’[1],…,C’[K-1])]=G_LT * Transpose[(C[0], …, C[L-1])]

显然中间符号数量 L=K+S+H
中间符号的计算可以表示为：C = (A^^-1)*D

源符号triple的生成使得对于任何K矩阵，A满秩，因此可逆。 这个计算可以通过对K个源符号C’[0], C’[1], …, C’[K-1]应用Raptor解码过程来实现，产生L个中间符号C[0], C[1], …, C[L-1] 。

5.4.3 Second Encoding Step: LT Encoding

  对L个中间符号C[0]、C[1]、…、C[L-1]，使用LTEcn来生成具有ESI的修复符号。

函数LTEnc[K, (C[0], C[1],…, C[L-1]), (d, a, b)]：

输入：
K：源块（子块）的源符号（或子符号）的数量。注意L从K中导出，而L’在Trip()中定义为大于或等于L的最小质整数。
(C[0], C[1],…, C[L-1])：L个中间符号（子符号）
(d, a, b)：d表示编码符号的度，a为[1,L’-1]之间的整数，b为[0,L’-1]之间的整数.

算法：
While (b >= L) do b = (b + a) % L’
Let result = C[b].
For j = 1,…,min(d-1,L-1) do
  b = (b + a) % L’
  While (b >= L) do b = (b + a) % L’
  result = result ^ C[b]
Return result

5.4.4 Generator

Random Generator： 给定X，i产生一个0~m-1之间的整数。
$\mathrm{Rand}[\mathrm{X},i,\mathrm{m}]=(\mathrm{V}0[(\mathrm{X}+\mathrm{i})\%256]\wedge \mathrm{V}1[(\mathrm{floor}(\mathrm{X}/256)+i)\%256])\%m$

其中V0V1为256个元素的数组，每个元素是一个4Byte的无符号整数（见5.6）。

Degree Generator: Deg[v]，给定一个$0\le v<2^{20}=1048576$，找到$f[j-1]\le v<f[j]$，令Deg[v] = d[j]

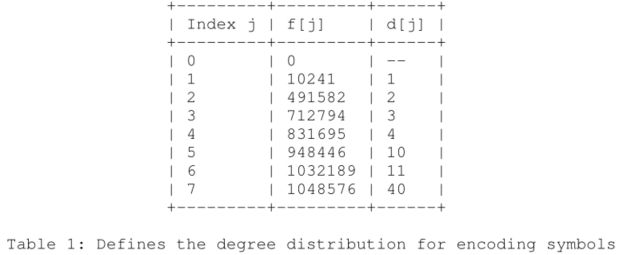
5.5 解码示例

  每个收到的编码符号可视为中间符号之间的方程值。从方程组和已知的中间符号之间的预编码关系来看，任何解方程的算法都可以成功解码中间符号，从而解码源符号。
  解码器知道它要解码的源块的结构，包括符号大小T和源块中符号的数量K。并可计算出预编码符号的总数L=K+S+H，并确定它们是如何从待解码的源块中产生的。

注意，如第5.3.2节所述，源数据包的最后一个源符号可能包括为FEC编码目的而添加的填充字节。 这些填充字节可能没有实际包括在发送的数据包中，因此在将符号传递给解码器之前，必须在收到的地方重新插入这些填充字节。

该部分后续更新（9.13留）

5.6 度分布

给出了两个表V0V1，每个元素是一个十进制的32位整数

5.7 Systematic Indices J(K)

for $\forall K\in [4,8192]$,J(K)属性：使得(d[0], a[0],
b[0]), …, (d[L-1], a[L-1], b[L-1])对应的中间符号唯一，使得A满秩。

标准中给出了一个表，J(K)的离散值。