机器学习练习 7 - K-means 和PCA（主成分分析）

机器学习练习 7 - K-means 和PCA（主成分分析）

在本练习中，我们将实现K-means聚类，并使用它来压缩图像。 我们将从一个简单的2D数据集开始，以了解K-means是如何工作的，然后我们将其应用于图像压缩。 我们还将对主成分分析进行实验，并了解如何使用它来找到面部图像的低维表示。

K-means 聚类

我们将实施和应用K-means到一个简单的二维数据集，以获得一些直观的工作原理。 K-means是一个迭代的，无监督的聚类算法，将类似的实例组合成簇。 该算法通过猜测每个簇的初始聚类中心开始，然后重复将实例分配给最近的簇，并重新计算该簇的聚类中心。 我们要实现的第一部分是找到数据中每个实例最接近的聚类中心的函数。

In [1]:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat
/opt/conda/lib/python3.6/importlib/_bootstrap.py:219: RuntimeWarning: numpy.dtype size changed, may indicate binary incompatibility. Expected 96, got 88
  return f(*args, **kwds)
/opt/conda/lib/python3.6/importlib/_bootstrap.py:219: RuntimeWarning: numpy.dtype size changed, may indicate binary incompatibility. Expected 96, got 88
  return f(*args, **kwds)
/opt/conda/lib/python3.6/site-packages/matplotlib/font_manager.py:232: UserWarning: Matplotlib is building the font cache using fc-list. This may take a moment.
  'Matplotlib is building the font cache using fc-list. '

In [2]:

def find_closest_centroids(X, centroids):
    m = X.shape[0]
    k = centroids.shape[0]
    idx = np.zeros(m)
    
    for i in range(m):
        min_dist = 1000000
        for j in range(k):
            dist = np.sum((X[i,:] - centroids[j,:]) ** 2)
            if dist < min_dist:
                min_dist = dist
                idx[i] = j
    
    return idx # 每个点所属的类

让我们来测试这个函数，以确保它的工作正常。 我们将使用练习中提供的测试用例。

In [3]:

data = loadmat('/home/kesci/input/andrew_ml_ex78376/ex7data2.mat')
X = data['X']
initial_centroids = np.array([[3, 3], [6, 2], [8, 5]])

idx = find_closest_centroids(X, initial_centroids)
idx[0:3]

Out[3]:

array([0., 2., 1.])

输出与文本中的预期值匹配（记住我们的数组是从零开始索引的，而不是从一开始索引的，所以值比练习中的值低一个）。 接下来，我们需要一个函数来计算簇的聚类中心。 聚类中心只是当前分配给簇的所有样本的平均值。

In [4]:

data2 = pd.DataFrame(data.get('X'), columns=['X1', 'X2'])
data2.head()

Out[4]:

	X1	X2
0	1.842080	4.607572
1	5.658583	4.799964
2	6.352579	3.290854
3	2.904017	4.612204
4	3.231979	4.939894

seaborn.lmplot

'''
seaborn.lmplot()方法用于将散点图绘制到FacetGrid上。

用法： seaborn.lmplot(x, y, data, hue=None, col=None, row=None, palette=None, col_wrap=None, height=5, aspect=1, markers=’o’, sharex=True, sharey=True, hue_order=None, col_order=None, row_order=None, legend=True, legend_out=True, x_estimator=None, x_bins=None, x_ci=’ci’, scatter=True, fit_reg=True, ci=95, n_boot=1000, units=None, seed=None, order=1, logistic=False, lowess=False, robust=False, logx=False, x_partial=None, y_partial=None, truncate=True, x_jitter=None, y_jitter=None, scatter_kws=None, line_kws=None, size=None)

参数：此方法接受下面描述的以下参数：

x, y：(可选)此参数是数据中的列名。

data:此参数是DataFrame。

hue, col, row:此参数是数据的定义子集，这些子集将绘制在网格的不同面上。请参阅* _order参数以控制此变量的级别顺序。

palette：(可选)此参数是调色板名称，列表或字典，用于不同级别的hue变量的颜色。应该是可以由color_palette()解释的内容，或者是将色相级别映射到matplotlib颜色的字典。

col_wrap:(可选)此参数为int类型，“Wrap”具有此宽度的列变量，以便列构面跨越多行。与行构面不兼容。

height:(可选)此参数是每个构面的高度(以英寸为单位)。

aspect:(可选)此参数是每个构面的纵横比，因此，aspect * height给出每个构面的宽度(以英寸为单位)。

markers:(可选)此参数是matplotlib标记代码或标记代码列表，散点图的标记。如果是列表，列表中的每个标记将用于每个级别的色相变量。

share{x, y}:(可选)此参数为布尔型‘col’或‘row’。如果为true，则构面将共享列的y轴和/或行的x轴。

{hue，col，row} _order：(可选)此参数是列表，是构面变量级别的顺序。默认情况下，这将是级别在数据中出现的顺序；如果变量是pandas类别，则将是类别顺序。

legend:(可选)此参数接受bool值，如果为True且有色相变量，请添加图例。

legend_out:(可选)此参数接受bool值，如果为True，则图形尺寸将被扩展，并且图例将绘制在右中图的外部。

x_estimator:(可选)可调用此参数以映射向量->标量，将此函数应用于x的每个唯一值并绘制结果估计。当x是离散变量时，这很有用。如果给出x_ci，则该估计将被引导并绘制置信区间。

x_bins:(可选)此参数为int或vector，将x变量绑定到离散的bin中，然后估计中心趋势和置信区间。这种装箱仅影响散点图的绘制方式；回归仍然适合原始数据。此参数被解释为evenly-sized(不需要间隔)的存储箱数或存储箱中心的位置。使用此参数时，表示x_estimator的默认值为numpy.mean。

x_ci:(可选)此参数为“ci”，“sd”，[0，100]中的int或“无”，为x的离散值绘制中心趋势时使用的置信区间的大小。如果为“ci”，则遵循ci参数的值。如果为“sd”，请跳过引导程序，并显示每个仓中观测值的标准偏差。

scatter:(可选)此参数接受bool值。如果为True，则使用基础观测值(或x_estimator值)绘制散点图。

fit_reg:(可选)此参数接受bool值。如果为True，则估计并绘制与x和y变量相关的回归模型。

ci:(可选)此参数为int，为[0，100]或无，回归估计的置信区间的大小。这将使用回归线周围的半透明带绘制。置信区间是使用自举估算的；对于大型数据集，建议将此参数设置为“无”以避免计算。

n_boot:(可选)此参数是用于估计ci的引导程序重采样数。缺省值试图平衡时间和稳定性。您可能想增加“final”版图的此值。

units:(可选)此参数是数据中的变量名称。如果x和y观测值嵌套在采样单位内，则可以在此处指定这些观测值。在通过执行对单元和观测值(单元内)都重新采样的多级引导程序来计算置信区间时，将考虑到这一点。否则，这不会影响回归的估计或绘制方式。

seed:(可选)此参数是int，numpy.random.Generator或numpy.random.RandomState，Seed或用于可重引导的随机数生成器。

order:(可选)此参数的阶数大于1，使用numpy.polyfit估计多项式回归。

logistic:(可选)此参数接受布尔值，如果为True，则假定y是二进制变量，并使用statsmodels估计逻辑回归模型。请注意，这比线性回归的计算量大得多，因此您可能希望减少引导程序重采样(n_boot)的次数或将ci设置为None。

lowess:(可选)此参数接受bool值，如果为True，则使用statsmodels估计非参数的lowess模型(局部加权线性回归)。请注意，目前无法为这种模型绘制置信区间。

robust:(可选)此参数接受布尔值，如果为True，则使用statsmodels估计稳健的回归。这将是de-weight个异常值。请注意，这比标准线性回归的计算量大得多，因此您可能希望减少引导程序重采样的次数(n_boot)或将ci设置为None。

logx:(可选)此参数接受布尔值。如果为True，则估计形式为y〜log(x)的线性回归，但在输入空间中绘制散点图和回归模型。请注意，x必须为正数才能起作用。

{x，y} _partial：(可选)此参数是数据或矩阵中的字符串，混淆变量以在绘制之前从x或y变量中回归。

truncate:(可选)此参数接受布尔值。如果为True，则回归线受数据限制的限制。如果为False，则延伸到x轴限制。

{x，y} _jitter：(可选)此参数是将此大小的均匀随机噪声添加到x或y变量中。拟合回归后，噪声会添加到数据副本中，并且只会影响散点图的外观。在绘制采用离散值的变量时，这可能会有所帮助。

{scatter，line} _kws：(可选)词典

返回值：此方法返回上面带有图的FacetGrid对象，以进行进一步调整。
'''

In [5]:

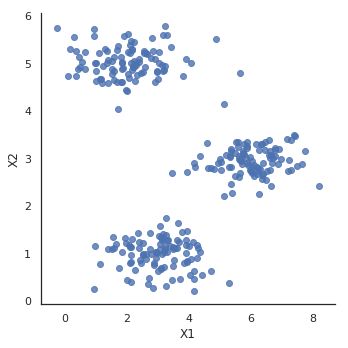
sb.set(context="notebook", style="white")
sb.lmplot('X1', 'X2', data=data2, fit_reg=False)
plt.show()

In [6]:

def compute_centroids(X, idx, k):
    m, n = X.shape
    centroids = np.zeros((k, n))
    
    for i in range(k):
        indices = np.where(idx == i)
        centroids[i,:] = (np.sum(X[indices,:], axis=1) / len(indices[0])).ravel() # (300,2) array 一维[[],[]]
        #indices tuple:1 默认取tuple前的array 同indices[0]
    
    return centroids # 每个类的中心点
'''
1.np.where(condition,x,y) 当where内有三个参数时，第一个参数表示条件，当条件成立时where方法返回x，当条件不成立时where返回y
2.np.where(condition) 当where内只有一个参数时，那个参数表示条件，当条件成立时，where返回的是每个符合condition条件元素的坐标,返回的是以元组的形式
'''

In [7]:

compute_centroids(X, idx, 3)

Out[7]:

array([[2.42830111, 3.15792418],
       [5.81350331, 2.63365645],
       [7.11938687, 3.6166844 ]])

此输出也符合练习中的预期值。
下一部分涉及实际运行该算法的一些迭代次数和可视化结果。
这个步骤是由于并不复杂，我将从头开始构建它。 为了运行算法，我们只需要在将样本分配给最近的簇并重新计算簇的聚类中心。

In [8]:

def run_k_means(X, initial_centroids, max_iters):
    m, n = X.shape
    k = initial_centroids.shape[0]
    idx = np.zeros(m)
    centroids = initial_centroids
    
    for i in range(max_iters):
        idx = find_closest_centroids(X, centroids)
        centroids = compute_centroids(X, idx, k)
    
    return idx, centroids

In [9]:

idx, centroids = run_k_means(X, initial_centroids, 10)

In [10]:

cluster1 = X[np.where(idx == 0)[0],:]
cluster2 = X[np.where(idx == 1)[0],:]
cluster3 = X[np.where(idx == 2)[0],:]

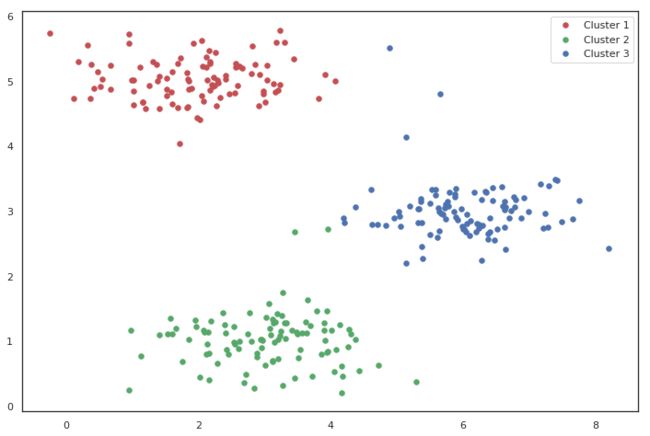
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(cluster1[:,0], cluster1[:,1], s=30, color='r', label='Cluster 1')
ax.scatter(cluster2[:,0], cluster2[:,1], s=30, color='g', label='Cluster 2')
ax.scatter(cluster3[:,0], cluster3[:,1], s=30, color='b', label='Cluster 3')
ax.legend()
plt.show()

我们跳过的一个步骤是初始化聚类中心的过程。 这可以影响算法的收敛。 我们的任务是创建一个选择随机样本并将其用作初始聚类中心的函数。

In [11]:

def init_centroids(X, k):
    m, n = X.shape
    centroids = np.zeros((k, n))
    idx = np.random.randint(0, m, k)
    
    for i in range(k):
        centroids[i,:] = X[idx[i],:]
    
    return centroids

'''
函数的作用是，返回一个随机整型数，其范围为[low, high)。如果没有写参数high的值，则返回[0,low)的值。

从random可以看出是产生随机数，randint可以看出是产生随机整数（int）

参数如下：

low: int
表示生成的数值大于等于low。
（hign = None时，生成的数值要在[0, low)区间内）
high: int (可选)
如果使用这个值，则生成的数值在[low, high)区间
size: int or tuple of ints(可选)
输出随机数组的尺寸，比如size = (m, n, k)，则输出数组的shape = (m, n, k)，数组中的每个元素均满足要求。size默认为None，仅仅返回满足要求的单一随机数。
dtype: dtype(可选)：
想要输出的格式。如int64、int等等
输出：

out: int or ndarray of ints
返回一个随机数或随机数数组
'''

In [12]:

init_centroids(X, 3)

Out[12]:

array([[4.1877442 , 2.89283463],
       [1.96547974, 1.2173076 ],
       [0.37963437, 5.26194729]])

我们的下一个任务是将K-means应用于图像压缩。 从下面的演示可以看到，我们可以使用聚类来找到最具代表性的少数颜色，并使用聚类分配将原始的24位颜色映射到较低维的颜色空间。

下面是我们要压缩的图像。

In [13]:

from IPython.display import Image
Image(filename='/home/kesci/input/andrew_ml_ex78376/bird_small.png')

Out[13]:

原始像素测像素点数值

In [14]:

image_data = loadmat('/home/kesci/input/andrew_ml_ex78376/bird_small.mat')
image_data

Out[14]:

{'__header__': b'MATLAB 5.0 MAT-file, Platform: GLNXA64, Created on: Tue Jun  5 04:06:24 2012',
 '__version__': '1.0',
 '__globals__': [],
 'A': array([[[219, 180, 103],
         [230, 185, 116],
         [226, 186, 110],
         ...,
         [ 14,  15,  13],
         [ 13,  15,  12],
         [ 12,  14,  12]],
 
        [[230, 193, 119],
         [224, 192, 120],
         [226, 192, 124],
         ...,
         [ 16,  16,  13],
         [ 14,  15,  10],
         [ 11,  14,   9]],
 
        [[228, 191, 123],
         [228, 191, 121],
         [220, 185, 118],
         ...,
         [ 14,  16,  13],
         [ 13,  13,  11],
         [ 11,  15,  10]],
 
        ...,
 
        [[ 15,  18,  16],
         [ 18,  21,  18],
         [ 18,  19,  16],
         ...,
         [ 81,  45,  45],
         [ 70,  43,  35],
         [ 72,  51,  43]],
 
        [[ 16,  17,  17],
         [ 17,  18,  19],
         [ 20,  19,  20],
         ...,
         [ 80,  38,  40],
         [ 68,  39,  40],
         [ 59,  43,  42]],
 
        [[ 15,  19,  19],
         [ 20,  20,  18],
         [ 18,  19,  17],
         ...,
         [ 65,  43,  39],
         [ 58,  37,  38],
         [ 52,  39,  34]]], dtype=uint8)}

In [15]:

A = image_data['A']
A.shape

Out[15]:

(128, 128, 3)

现在我们需要对数据应用一些预处理，并将其提供给K-means算法。

In [16]:

# normalize value ranges
A = A / 255.

# reshape the array
X = np.reshape(A, (A.shape[0] * A.shape[1], A.shape[2]))
X.shape

Out[16]:

(16384, 3)

In [17]:

# randomly initialize the centroids
initial_centroids = init_centroids(X, 16)  # 16个类

# run the algorithm
idx, centroids = run_k_means(X, initial_centroids, 10) # 10次迭代

# get the closest centroids one last time
idx = find_closest_centroids(X, centroids) 

# map each pixel to the centroid value
X_recovered = centroids[idx.astype(int),:]  # 每个像素的类的中心点
X_recovered.shape

Out[17]:

(16384, 3)

In [18]:

# reshape to the original dimensions
X_recovered = np.reshape(X_recovered, (A.shape[0], A.shape[1], A.shape[2]))
X_recovered.shape

Out[18]:

(128, 128, 3)

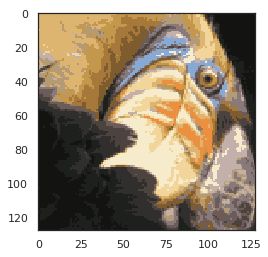
In [19]:

plt.imshow(X_recovered)
plt.show()

'''
图像数据。支持的数组形状是：

（M，N） ：带有标量数据的图像。数据可视化使用色彩图。
（M，N，3） ：具有RGB值的图像（float或uint8）。
（M，N，4） ：具有RGBA值的图像（float或uint8），即包括透明度。
前两个维度（M，N）定义了行和列图片，即图片的高和宽；
RGB（A）值应该在浮点数[0, …, 1]的范围内,或者
整数[0, … ,255]。超出范围的值将被剪切为这些界限。
'''

您可以看到我们对图像进行了压缩，但图像的主要特征仍然存在。 这就是K-means。 下面我们来用scikit-learn来实现K-means。

In [20]:

from skimage import io

# cast to float, you need to do this otherwise the color would be weird after clustring
pic = io.imread('/home/kesci/input/andrew_ml_ex78376/bird_small.png') / 255. # RGB
io.imshow(pic)
plt.show()

In [21]:

pic.shape

Out[21]:

(128, 128, 3)

In [22]:

# serialize data
data = pic.reshape(128*128, 3)

In [23]:

data.shape

Out[23]:

(16384, 3)

In [24]:

from sklearn.cluster import KMeans#导入kmeans库

model = KMeans(n_clusters=16, n_init=100)
'''
1 参数

n_clusters：整形，缺省值=8 【生成的聚类数，即产生的质心（centroids）数。】

max_iter：整形，缺省值=300 【执行一次k-means算法所进行的最大迭代数。】

n_init：整形，缺省值=10 【用不同的质心初始化值运行算法的次数，最终解是在inertia意义下选出的最优结果。】
init：有三个可选值：’k-means++’， ‘random’，或者传递一个ndarray向量。
此参数指定初始化方法，默认值为 ‘k-means++’。
（１）‘k-means++’ 用一种特殊的方法选定初始质心从而能加速迭代过程的收敛（即上文中的k-means++介绍）
（２）‘random’ 随机从训练数据中选取初始质心。
（３）如果传递的是一个ndarray，则应该形如 (n_clusters, n_features) 并给出初始质心。

precompute_distances：三个可选值，‘auto’，True 或者 False。
预计算距离，计算速度更快但占用更多内存。
（１）‘auto’：如果 样本数乘以聚类数大于 12million 的话则不予计算距离。This corresponds to about 100MB overhead per job using double precision.
（２）True：总是预先计算距离。
（３）False：永远不预先计算距离。

tol：float形，默认值= 1e-4　与inertia结合来确定收敛条件。

n_jobs：整形数。　指定计算所用的进程数。内部原理是同时进行n_init指定次数的计算。
（１）若值为 -1，则用所有的CPU进行运算。若值为1，则不进行并行运算，这样的话方便调试。
（２）若值小于-1，则用到的CPU数为(n_cpus + 1 + n_jobs)。因此如果 n_jobs值为-2，则用到的CPU数为总CPU数减1。

random_state：整形或 numpy.RandomState 类型，可选
用于初始化质心的生成器（generator）。如果值为一个整数，则确定一个seed。此参数默认值为numpy的随机数生成器。
-copy_x：布尔型，默认值=True
当我们precomputing distances时，将数据中心化会得到更准确的结果。如果把此参数值设为True，则原始数据不会被改变。如果是False，则会直接在原始数据上做修改并在函数返回值时将其还原。但是在计算过程中由于有对数据均值的加减运算，所以数据返回后，原始数据和计算前可能会有细小差别。

2 属性

cluster_centers_：向量，[n_clusters, n_features] (聚类中心的坐标)

Labels_: 每个点的分类

inertia_：float形
每个点到其簇的质心的距离之和。

Notes：
　　这个k-means运用了 Lioyd’s 算法,平均计算复杂度是 O(knT)，其中n是样本量，T是迭代次数。
　　计算复杂读在最坏的情况下为 O(n^(k+2/p))，其中n是样本量，p是特征个数。
　　在实践中，k-means算法时非常快的，属于可实践的算法中最快的那一类。但是它的解只是由特定初始值所产生的局部解。所以为了让结果更准确真实，在实践中要用不同的初始值重复几次才可以。

3 Methods

fit(X[,y]): 计算k-means聚类。

fit_predict(X[,y]): 计算簇质心并给每个样本预测类别。

fit_transform(X[,y])：计算簇并 transform X to cluster-distance space。

get_params([deep])：取得估计器的参数。

predict(X): 给每个样本估计最接近的簇。

score(X[,y]): 计算聚类误差

set_params(**params): 为这个估计器手动设定参数。

transform(X[,y]): 将X转换为群集距离空间。 　
在新空间中，每个维度都是到集群中心的距离。请注意，即使X是稀疏的，转换返回的数组通常也是密集的。
'''

In [25]:

model.fit(data)

Out[25]:

KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
    n_clusters=16, n_init=100, n_jobs=-1, precompute_distances='auto',
    random_state=None, tol=0.0001, verbose=0)

In [26]:

centroids = model.cluster_centers_
print(centroids.shape)

C = model.predict(data)
print(C.shape)
(16, 3)
(16384,)

In [27]:

centroids[C].shape

Out[27]:

(16384, 3)

In [28]:

compressed_pic = centroids[C].reshape((128,128,3))

In [29]:

fig, ax = plt.subplots(1, 2)
ax[0].imshow(pic)
ax[1].imshow(compressed_pic)
plt.show()

Principal component analysis（主成分分析）

PCA 减少$n$维到$k$维：

第一步是均值归一化。我们需要计算出所有特征的均值，然后令 $x_j=x_j-{\mu }_j$。如果特征是在不同的数量级上，我们还需要将其除以标准差 ${\sigma }^2$。

第二步是计算协方差矩阵（covariance matrix）$\Sigma$：
$$\sum =\frac{1}{m}\sum _{i=1}^n\left(x^{(i)}\right){\left(x^{(i)}\right)}^T$$

第三步是计算协方差矩阵$\Sigma$的特征向量（eigenvectors）:

在 Octave 里我们可以利用奇异值分解（singular value decomposition）来求解，[U, S, V]= svd(sigma)。

对于一个 $n\times n$维度的矩阵，上式中的$U$是一个具有与数据之间最小投射误差的方向向量构成的矩阵。如果我们希望将数据从$n$维降至$k$维，我们只需要从$U$中选取前$k$个向量，获得一个$n\times k$维度的矩阵，我们用$U_{reduce}$表示，然后通过如下计算获得要求的新特征向量$z^{(i)}$:
$$z^{(i)}=U_{reduce}^T\ast x^{(i)}$$

其中$x$是$n\times 1$维的，因此结果为$k\times 1$维度。注，我们不对方差特征进行处理。

PCA是在数据集中找到“主成分”或最大方差方向的线性变换。 它可以用于降维。 在本练习中，我们首先负责实现PCA并将其应用于一个简单的二维数据集，以了解它是如何工作的。 我们从加载和可视化数据集开始。

主要成分分析是减少投射的平均均方误差：
$$\frac{1}{m}\sum _{i=1}^m{\Vert x^{\left(i\right)}-x_{approx}^{\left(i\right)}\Vert }^2$$

训练集的方差为：
$$\frac{1}{m}\sum _{i=1}^m{\Vert x^{\left(i\right)}\Vert }^2$$

我们希望在平均均方误差与训练集方差的比例尽可能小的情况下选择尽可能小的$k$值。

如果我们希望这个比例小于1%，就意味着原本数据的偏差有99%都保留下来了，如果我们选择保留95%的偏差，便能非常显著地降低模型中特征的维度了。

我们可以先令$k=1$，然后进行主要成分分析，获得$U_{reduce}$和$z$，然后计算比例是否小于1%。如果不是的话再令$k=2$，如此类推，直到找到可以使得比例小于1%的最小$k$ 值（原因是各个特征之间通常情况存在某种相关性）。

还有一些更好的方式来选择$k$，当我们在Octave中调用svd函数的时候，我们获得三个参数：[U, S, V] = svd(sigma)

其中的$S$是一个$n\times n$的矩阵，只有对角线上有值，而其它单元都是0，我们可以使用这个矩阵来计算平均均方误差与训练集方差的比例：
$$\frac{\frac{1}{m}{\sum }_{i=1}^m{\Vert x^{\left(i\right)}-x_{approx}^{\left(i\right)}\Vert }^2}{\frac{1}{m}{\sum }_{i=1}^m{\Vert x^{(i)}\Vert }^2}=1-\frac{{\Sigma }_{i=1}^k{S}_{ii}}{{\Sigma }_{i=1}^m{S}_{ii}}\le 1\%$$

也就是：
$$\frac{{\Sigma }_{i=1}^k{s}_{ii}}{{\Sigma }_{i=1}^n{s}_{ii}}\ge 0.99$$

在压缩过数据后，我们可以采用如下方法来近似地获得原有的特征：
$$x_{approx}^{\left(i\right)}=U_{reduce}{z}^{(i)}$$

注：如果我们有交叉验证集合测试集，也采用对训练集学习而来的$U_{reduce}$。

错误的主要成分分析情况：一个常见错误使用主要成分分析的情况是，将其用于减少过拟合（减少了特征的数量）。这样做非常不好，不如尝试正则化处理。原因在于主要成分分析只是近似地丢弃掉一些特征，它并不考虑任何与结果变量有关的信息，因此可能会丢失非常重要的特征。然而当我们进行正则化处理时，会考虑到结果变量，不会丢掉重要的数据。

另一个常见的错误是，默认地将主要成分分析作为学习过程中的一部分，这虽然很多时候有效果，最好还是从所有原始特征开始，只在有必要的时候（算法运行太慢或者占用太多内存）才考虑采用主要成分分析。

In [30]:

data = loadmat('/home/kesci/input/andrew_ml_ex78376/ex7data1.mat')
data

Out[30]:

{'__header__': b'MATLAB 5.0 MAT-file, Platform: PCWIN64, Created on: Mon Nov 14 22:41:44 2011',
 '__version__': '1.0',
 '__globals__': [],
 'X': array([[3.38156267, 3.38911268],
        [4.52787538, 5.8541781 ],
        [2.65568187, 4.41199472],
        [2.76523467, 3.71541365],
        [2.84656011, 4.17550645],
        [3.89067196, 6.48838087],
        [3.47580524, 3.63284876],
        [5.91129845, 6.68076853],
        [3.92889397, 5.09844661],
        [4.56183537, 5.62329929],
        [4.57407171, 5.39765069],
        [4.37173356, 5.46116549],
        [4.19169388, 4.95469359],
        [5.24408518, 4.66148767],
        [2.8358402 , 3.76801716],
        [5.63526969, 6.31211438],
        [4.68632968, 5.6652411 ],
        [2.85051337, 4.62645627],
        [5.1101573 , 7.36319662],
        [5.18256377, 4.64650909],
        [5.70732809, 6.68103995],
        [3.57968458, 4.80278074],
        [5.63937773, 6.12043594],
        [4.26346851, 4.68942896],
        [2.53651693, 3.88449078],
        [3.22382902, 4.94255585],
        [4.92948801, 5.95501971],
        [5.79295774, 5.10839305],
        [2.81684824, 4.81895769],
        [3.88882414, 5.10036564],
        [3.34323419, 5.89301345],
        [5.87973414, 5.52141664],
        [3.10391912, 3.85710242],
        [5.33150572, 4.68074235],
        [3.37542687, 4.56537852],
        [4.77667888, 6.25435039],
        [2.6757463 , 3.73096988],
        [5.50027665, 5.67948113],
        [1.79709714, 3.24753885],
        [4.3225147 , 5.11110472],
        [4.42100445, 6.02563978],
        [3.17929886, 4.43686032],
        [3.03354125, 3.97879278],
        [4.6093482 , 5.879792  ],
        [2.96378859, 3.30024835],
        [3.97176248, 5.40773735],
        [1.18023321, 2.87869409],
        [1.91895045, 5.07107848],
        [3.95524687, 4.5053271 ],
        [5.11795499, 6.08507386]])}

In [31]:

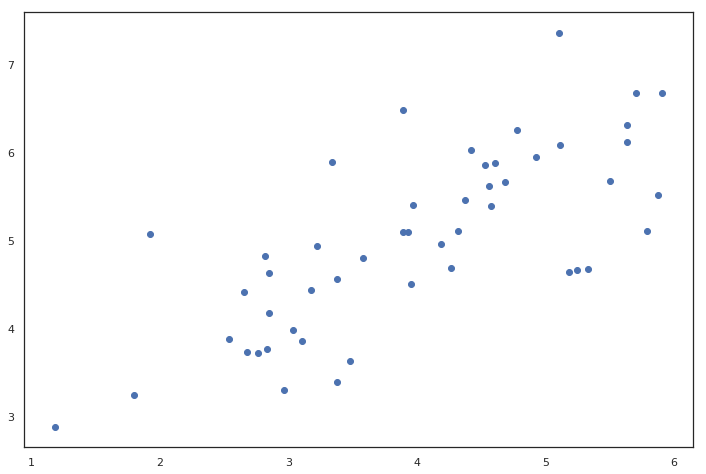
X = data['X']

fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(X[:, 0], X[:, 1])
plt.show()

PCA的算法相当简单。 在确保数据被归一化之后，输出仅仅是原始数据的协方差矩阵的奇异值分解。

In [32]:

def pca(X):
    # normalize the features
    X = (X - X.mean()) / X.std()
    
    # compute the covariance matrix
    X = np.matrix(X)
    cov = (X.T * X) / X.shape[0] # 均值为0 省略
    
    # perform SVD
    U, S, V = np.linalg.svd(cov)
    
    return U, S, V

'''
参数：
a是一个形如(M,N)矩阵

full_matrices的取值是为0或者1，默认值为1，这时u的大小为(M,M)，v的大小为(N,N) 。否则u的大小为(M,K)，v的大小为(K,N) ，K=min(M,N)。

compute_uv的取值是为0或者1，默认值为1，表示计算u,s,v。为0的时候只计算s。

返回值：

总共有三个返回值u,s,v
u大小为(M,M)，s大小为(M,N)，v大小为(N,N)。

A = u*s*v

其中s是对矩阵a的奇异值分解。s除了对角元素不为0，其他元素都为0，并且对角元素从大到小排列。s中有n个奇异值，一般排在后面的比较接近0，所以仅保留比较大的r个奇异值。
'''

In [33]:

U, S, V = pca(X)
U, S, V

Out[33]:

(matrix([[-0.79241747, -0.60997914],
         [-0.60997914,  0.79241747]]),
 array([1.43584536, 0.56415464]),
 matrix([[-0.79241747, -0.60997914],
         [-0.60997914,  0.79241747]]))

现在我们有主成分**（矩阵U）**，我们可以用这些来将原始数据投影到一个较低维的空间中。 对于这个任务，我们将实现一个计算投影并且仅选择顶部K个分量的函数，有效地减少了维数。

In [34]:

def project_data(X, U, k):
    U_reduced = U[:,:k]
    return np.dot(X, U_reduced)

In [35]:

Z = project_data(X, U, 1)
Z

Out[35]:

matrix([[-4.74689738],
        [-7.15889408],
        [-4.79563345],
        [-4.45754509],
        [-4.80263579],
        [-7.04081342],
        [-4.97025076],
        [-8.75934561],
        [-6.2232703 ],
        [-7.04497331],
        [-6.91702866],
        [-6.79543508],
        [-6.3438312 ],
        [-6.99891495],
        [-4.54558119],
        [-8.31574426],
        [-7.16920841],
        [-5.08083842],
        [-8.54077427],
        [-6.94102769],
        [-8.5978815 ],
        [-5.76620067],
        [-8.2020797 ],
        [-6.23890078],
        [-4.37943868],
        [-5.56947441],
        [-7.53865023],
        [-7.70645413],
        [-5.17158343],
        [-6.19268884],
        [-6.24385246],
        [-8.02715303],
        [-4.81235176],
        [-7.07993347],
        [-5.45953289],
        [-7.60014707],
        [-4.39612191],
        [-7.82288033],
        [-3.40498213],
        [-6.54290343],
        [-7.17879573],
        [-5.22572421],
        [-4.83081168],
        [-7.23907851],
        [-4.36164051],
        [-6.44590096],
        [-2.69118076],
        [-4.61386195],
        [-5.88236227],
        [-7.76732508]])

我们也可以通过反向转换步骤来恢复原始数据。

In [36]:

def recover_data(Z, U, k):
    U_reduced = U[:,:k]
    return np.dot(Z, U_reduced.T)

In [37]:

X_recovered = recover_data(Z, U, 1)
X_recovered

Out[37]:

matrix([[3.76152442, 2.89550838],
        [5.67283275, 4.36677606],
        [3.80014373, 2.92523637],
        [3.53223661, 2.71900952],
        [3.80569251, 2.92950765],
        [5.57926356, 4.29474931],
        [3.93851354, 3.03174929],
        [6.94105849, 5.3430181 ],
        [4.93142811, 3.79606507],
        [5.58255993, 4.29728676],
        [5.48117436, 4.21924319],
        [5.38482148, 4.14507365],
        [5.02696267, 3.8696047 ],
        [5.54606249, 4.26919213],
        [3.60199795, 2.77270971],
        [6.58954104, 5.07243054],
        [5.681006  , 4.37306758],
        [4.02614513, 3.09920545],
        [6.76785875, 5.20969415],
        [5.50019161, 4.2338821 ],
        [6.81311151, 5.24452836],
        [4.56923815, 3.51726213],
        [6.49947125, 5.00309752],
        [4.94381398, 3.80559934],
        [3.47034372, 2.67136624],
        [4.41334883, 3.39726321],
        [5.97375815, 4.59841938],
        [6.10672889, 4.70077626],
        [4.09805306, 3.15455801],
        [4.90719483, 3.77741101],
        [4.94773778, 3.80861976],
        [6.36085631, 4.8963959 ],
        [3.81339161, 2.93543419],
        [5.61026298, 4.31861173],
        [4.32622924, 3.33020118],
        [6.02248932, 4.63593118],
        [3.48356381, 2.68154267],
        [6.19898705, 4.77179382],
        [2.69816733, 2.07696807],
        [5.18471099, 3.99103461],
        [5.68860316, 4.37891565],
        [4.14095516, 3.18758276],
        [3.82801958, 2.94669436],
        [5.73637229, 4.41568689],
        [3.45624014, 2.66050973],
        [5.10784454, 3.93186513],
        [2.13253865, 1.64156413],
        [3.65610482, 2.81435955],
        [4.66128664, 3.58811828],
        [6.1549641 , 4.73790627]])

In [38]:

fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(list(X_recovered[:, 0]), list(X_recovered[:, 1]))
plt.show()

请注意，第一主成分的投影轴基本上是数据集中的对角线。 当我们将数据减少到一个维度时，我们失去了该对角线周围的变化，所以在我们的再现中，一切都沿着该对角线。

我们在此练习中的最后一个任务是将PCA应用于脸部图像。 通过使用相同的降维技术，我们可以使用比原始图像少得多的数据来捕获图像的“本质”。

In [39]:

faces = loadmat('/home/kesci/input/andrew_ml_ex78376/ex7faces.mat')
X = faces['X']
X.shape

Out[39]:

(5000, 1024)

In [40]:

def plot_n_image(X, n):
    """ plot first n images
    n has to be a square number
    """
    pic_size = int(np.sqrt(X.shape[1]))
    grid_size = int(np.sqrt(n))

    first_n_images = X[:n, :]

    fig, ax_array = plt.subplots(nrows=grid_size, ncols=grid_size,
                                    sharey=True, sharex=True, figsize=(8, 8))

    for r in range(grid_size):
        for c in range(grid_size):
            ax_array[r, c].imshow(first_n_images[grid_size * r + c].reshape((pic_size, pic_size)))
            plt.xticks(np.array([]))
            plt.yticks(np.array([]))

练习代码包括一个将渲染数据集中的前100张脸的函数。 而不是尝试在这里重新生成，您可以在练习文本中查看他们的样子。 我们至少可以很容易地渲染一个图像。

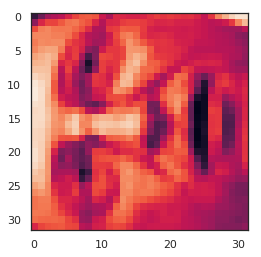
In [41]:

face = np.reshape(X[3,:], (32, 32))

In [42]:

plt.imshow(face)
plt.show()

看起来很糟糕。 这些只有32 x 32灰度的图像（它也是侧面渲染，但我们现在可以忽略）。 我们的下一步是在面数据集上运行PCA，并取得前100个主要特征。

In [43]:

U, S, V = pca(X)
Z = project_data(X, U, 100)

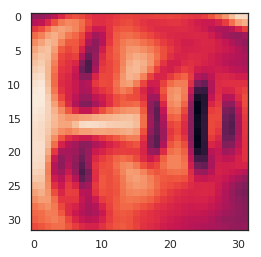
现在我们可以尝试恢复原来的结构并再次渲染。

In [44]:

X_recovered = recover_data(Z, U, 100)
face = np.reshape(X_recovered[3,:], (32, 32))
plt.imshow(face)
plt.show()

请注意，我们失去了一些细节，尽管没有像您预期的维度数量减少10倍。

最后练习7.在最后的练习中，我们将实现异常检测算法，并使用协同过滤构建推荐系统。