吴恩达机器学习ex7 python实现
K-Means聚类
我们将实施和应用K-means到一个简单的二维数据集,以获得一些直观的工作原理。
K-means聚类算法2维实现
寻找最近的聚类中心
我们要实现的第一部分是找到数据中每个实例最接近的聚类中心的函数。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat
data = loadmat('ex7data2.mat')
X = data['X']
X[:3]
array([[1.84207953, 4.6075716 ],
[5.65858312, 4.79996405],
[6.35257892, 3.2908545 ]])
def find_closest_cent(X,cent):
'''输入数据集X和聚类中心数组,找到离数据X最近的聚类中心'''
m = X.shape[0]
k = cent.shape[0]
idx = np.zeros(m)
for i in range(m):
min_distance = 1000000000
for j in range(k):
distance = np.sum((X[i,:]-cent[j,:])**2)
if distance < min_distance:
min_distance = distance
idx[i] = j
return idx
initial_cent = np.array([[3,3],[6,2],[8,5]])
idx = find_closest_cent(X,initial_cent)
idx[:3]
array([0., 2., 1.])
计算簇的聚类中心
即计算每个簇的所有样本的平均值
data2 = pd.DataFrame(data.get('X'),columns = ['x1','x2'])
data2.head()
| x1 | x2 | |
|---|---|---|
| 0 | 1.842080 | 4.607572 |
| 1 | 5.658583 | 4.799964 |
| 2 | 6.352579 | 3.290854 |
| 3 | 2.904017 | 4.612204 |
| 4 | 3.231979 | 4.939894 |
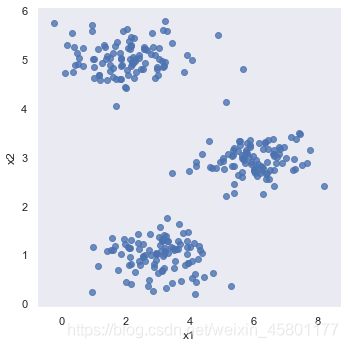
#数据可视化
sb.set(context = 'notebook',style='dark')
sb.lmplot('x1','x2',data=data2,fit_reg=False)
plt.show()
def compute_cent(X,idx,k):
'''给出样本集和分类集以及粗类中心个数,返回更新后的聚类中心'''
m,n = X.shape
cent = np.zeros((k,n))
for i in range(k):
ids = np.where(idx==i)
cent[i,:] = (np.sum(X[ids,:],axis=1)/len(ids[0])).ravel()
return cent
compute_cent(X,idx,3)
array([[2.42830111, 3.15792418],
[5.81350331, 2.63365645],
[7.11938687, 3.6166844 ]])
迭代已有算法
def run_k_means(X,init_cent,max_iters):
m,n = X.shape
k = init_cent.shape[0]
idx = np.zeros(m)
cent = init_cent
for i in range(max_iters):
idx = find_closest_cent(X,cent)
cent = compute_cent(X,idx,k)
return idx,cent
idx,cent = run_k_means(X,initial_cent,20)
cluster0 = X[np.where(idx == 0)[0],:]
cluster1 = X[np.where(idx == 1)[0],:]
cluster2 = X[np.where(idx == 2)[0],:]
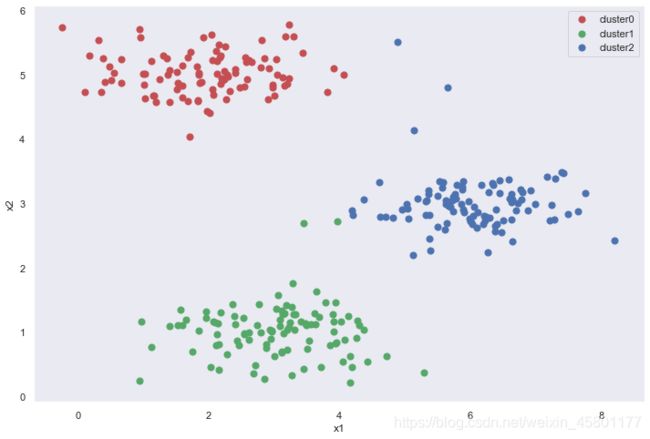
fig,ax = plt.subplots(figsize=(12,8))
ax.scatter(cluster0[:,0],cluster0[:,1],s=50,c='r',label='cluster0')
ax.scatter(cluster1[:,0],cluster1[:,1],s=50,c='g',label='cluster1')
ax.scatter(cluster2[:,0],cluster2[:,1],s=50,c='b',label='cluster2')
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.legend()
plt.show()
可以看出,因为初始聚类中心的确定导致算法并不是完全正确,所以我们用随机初始化创造新的初始聚类中心,观察最终结果。
def init_cent(X,k):
m,n = X.shape
cent = np.zeros((k,n))
idx = np.random.randint(0,m,k)
for i in range(k):
cent[i,:] = X[idx[i],:]
return cent
initial_cent2 = init_cent(X,3)
initial_cent2
array([[5.31712478, 2.81741356],
[6.00506534, 2.72784171],
[2.40304747, 5.08147326]])
idx,cent = run_k_means(X,initial_cent2,20)
cluster0 = X[np.where(idx == 0)[0],:]
cluster1 = X[np.where(idx == 1)[0],:]
cluster2 = X[np.where(idx == 2)[0],:]
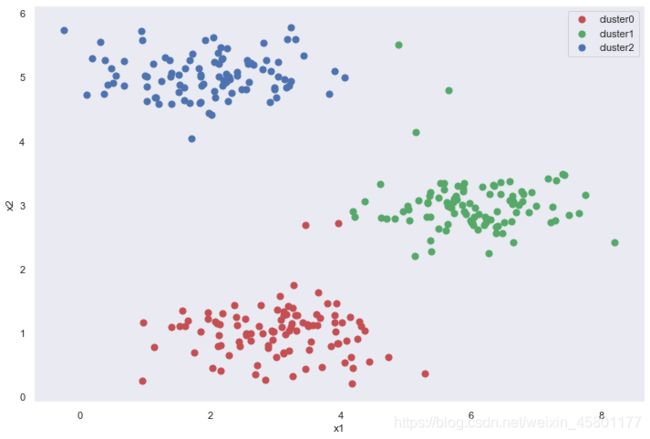
fig,ax = plt.subplots(figsize=(12,8))
ax.scatter(cluster0[:,0],cluster0[:,1],s=50,c='r',label='cluster0')
ax.scatter(cluster1[:,0],cluster1[:,1],s=50,c='g',label='cluster1')
ax.scatter(cluster2[:,0],cluster2[:,1],s=50,c='b',label='cluster2')
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.legend()
plt.show()
虽然一次随机初始化可能不能得到理想的结果,但是经过多次随机初始化并取综合情况,能得到相对比较合理的结果。
图像压缩
我们可以使用聚类来实现图片压缩。我们知道每张图片都是由许多像素点组成,每个像素点由不同的三原色的值组成。我们可以选择一定数量的三原色组合(即一定数量的颜色),通过聚类算法找到最具代表性的少数颜色,并使用聚类分配将原始的24位颜色映射到较低维的颜色空间。
手动实现K-Means
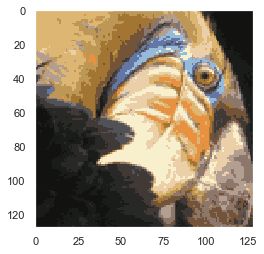
from IPython.display import Image
Image(filename='bird_small.png')
image = loadmat('bird_small.mat')
image
{'A': array([[[219, 180, 103],
[230, 185, 116],
[226, 186, 110],
...,
[ 14, 15, 13],
[ 13, 15, 12],
[ 12, 14, 12]],
[[230, 193, 119],
[224, 192, 120],
[226, 192, 124],
...,
[ 16, 16, 13],
[ 14, 15, 10],
[ 11, 14, 9]],
[[228, 191, 123],
[228, 191, 121],
[220, 185, 118],
...,
[ 14, 16, 13],
[ 13, 13, 11],
[ 11, 15, 10]],
...,
[[ 15, 18, 16],
[ 18, 21, 18],
[ 18, 19, 16],
...,
[ 81, 45, 45],
[ 70, 43, 35],
[ 72, 51, 43]],
[[ 16, 17, 17],
[ 17, 18, 19],
[ 20, 19, 20],
...,
[ 80, 38, 40],
[ 68, 39, 40],
[ 59, 43, 42]],
[[ 15, 19, 19],
[ 20, 20, 18],
[ 18, 19, 17],
...,
[ 65, 43, 39],
[ 58, 37, 38],
[ 52, 39, 34]]], dtype=uint8),
'__globals__': [],
'__header__': b'MATLAB 5.0 MAT-file, Platform: GLNXA64, Created on: Tue Jun 5 04:06:24 2012',
'__version__': '1.0'}
A = image['A']
A.shape
(128, 128, 3)
#归一化
A = A/255.
#数据重组
X = np.reshape(A,(A.shape[0]*A.shape[1],A.shape[2]))
X.shape
(16384, 3)
#随机初始化聚类中心
init_cent = init_cent(X,16)
idx,cent = run_k_means(X,init_cent,20)
X_recovered = cent[idx.astype(int),:]
X_recovered.shape
(16384, 3)
#重组回图片
X_recovered = np.reshape(X_recovered,(A.shape[0],A.shape[1],A.shape[2]))
X_recovered.shape
(128, 128, 3)
plt.imshow(X_recovered)
plt.show()
使用Sklearn实现K-Means
from skimage import io
pic = io.imread('bird_small.png')/255.
io.imshow(pic)
plt.show()
data = pic.reshape(128*128,3)
data.shape
(16384, 3)
from sklearn.cluster import KMeans
model = KMeans(n_clusters = 16,n_init=100,n_jobs=-1)
model.fit(data)
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
n_clusters=16, n_init=100, n_jobs=-1, precompute_distances='auto',
random_state=None, tol=0.0001, verbose=0)
cent = model.cluster_centers_
C = model.predict(data)
cent.shape,C.shape,cent[C].shape
((16, 3), (16384,), (16384, 3))
recovered = cent[C].reshape((128,128,3))
fig,ax = plt.subplots(1,2)
ax[0].imshow(pic)
ax[1].imshow(recovered)
plt.show()
主成成分分析
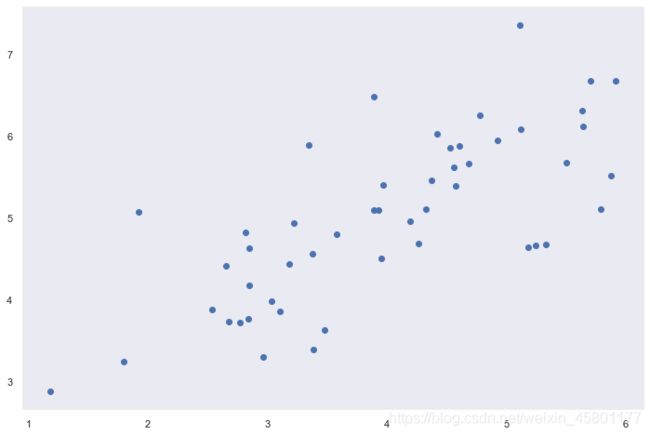
PCA是在数据集中找到“主成分”或最大方差方向的线性变换。 它可以用于降维。 在本练习中,我们首先负责实现PCA并将其应用于一个简单的二维数据集,以了解它是如何工作的。 我们从加载和可视化数据集开始。
data = loadmat('ex7data1.mat')
data
{'X': array([[3.38156267, 3.38911268],
[4.52787538, 5.8541781 ],
[2.65568187, 4.41199472],
[2.76523467, 3.71541365],
[2.84656011, 4.17550645],
[3.89067196, 6.48838087],
[3.47580524, 3.63284876],
[5.91129845, 6.68076853],
[3.92889397, 5.09844661],
[4.56183537, 5.62329929],
[4.57407171, 5.39765069],
[4.37173356, 5.46116549],
[4.19169388, 4.95469359],
[5.24408518, 4.66148767],
[2.8358402 , 3.76801716],
[5.63526969, 6.31211438],
[4.68632968, 5.6652411 ],
[2.85051337, 4.62645627],
[5.1101573 , 7.36319662],
[5.18256377, 4.64650909],
[5.70732809, 6.68103995],
[3.57968458, 4.80278074],
[5.63937773, 6.12043594],
[4.26346851, 4.68942896],
[2.53651693, 3.88449078],
[3.22382902, 4.94255585],
[4.92948801, 5.95501971],
[5.79295774, 5.10839305],
[2.81684824, 4.81895769],
[3.88882414, 5.10036564],
[3.34323419, 5.89301345],
[5.87973414, 5.52141664],
[3.10391912, 3.85710242],
[5.33150572, 4.68074235],
[3.37542687, 4.56537852],
[4.77667888, 6.25435039],
[2.6757463 , 3.73096988],
[5.50027665, 5.67948113],
[1.79709714, 3.24753885],
[4.3225147 , 5.11110472],
[4.42100445, 6.02563978],
[3.17929886, 4.43686032],
[3.03354125, 3.97879278],
[4.6093482 , 5.879792 ],
[2.96378859, 3.30024835],
[3.97176248, 5.40773735],
[1.18023321, 2.87869409],
[1.91895045, 5.07107848],
[3.95524687, 4.5053271 ],
[5.11795499, 6.08507386]]),
'__globals__': [],
'__header__': b'MATLAB 5.0 MAT-file, Platform: PCWIN64, Created on: Mon Nov 14 22:41:44 2011',
'__version__': '1.0'}
X = data['X']
fig,ax = plt.subplots(figsize=(12,8))
ax.scatter(X[:,0],X[:,1])
plt.show()
PCA算法
在数据完成归一化后,通过协方差矩阵的奇异值分解可以很容易得到输出
def PCA(X):
X = (X-X.mean()) / X.std()
X = np.matrix(X)
cov = (X.T * X) / X.shape[0]
U,S,V = np.linalg.svd(cov)
return U,S,V
U,S,V = PCA(X)
U,S,V
(matrix([[-0.79241747, -0.60997914],
[-0.60997914, 0.79241747]]),
array([1.43584536, 0.56415464]),
matrix([[-0.79241747, -0.60997914],
[-0.60997914, 0.79241747]]))
U就是我们需要的新特征,即主成分。我们用这些新特征把原始数据投影到新的地位空间中去。我们仅需编写选择前k个主成分,并计算投影的函数即可
def project_data(X,U,k):
U_reduced = U[:,:k]
return np.dot(X,U_reduced)
Z = project_data(X,U,1)
Z
matrix([[-4.74689738],
[-7.15889408],
[-4.79563345],
[-4.45754509],
[-4.80263579],
[-7.04081342],
[-4.97025076],
[-8.75934561],
[-6.2232703 ],
[-7.04497331],
[-6.91702866],
[-6.79543508],
[-6.3438312 ],
[-6.99891495],
[-4.54558119],
[-8.31574426],
[-7.16920841],
[-5.08083842],
[-8.54077427],
[-6.94102769],
[-8.5978815 ],
[-5.76620067],
[-8.2020797 ],
[-6.23890078],
[-4.37943868],
[-5.56947441],
[-7.53865023],
[-7.70645413],
[-5.17158343],
[-6.19268884],
[-6.24385246],
[-8.02715303],
[-4.81235176],
[-7.07993347],
[-5.45953289],
[-7.60014707],
[-4.39612191],
[-7.82288033],
[-3.40498213],
[-6.54290343],
[-7.17879573],
[-5.22572421],
[-4.83081168],
[-7.23907851],
[-4.36164051],
[-6.44590096],
[-2.69118076],
[-4.61386195],
[-5.88236227],
[-7.76732508]])
恢复近似原始数据
def recover_data(Z,U,k):
U_reduced = U[:,:k]
return np.dot(Z,U_reduced.T)
X_recovered = recover_data(Z,U,1)
X_recovered
matrix([[3.76152442, 2.89550838],
[5.67283275, 4.36677606],
[3.80014373, 2.92523637],
[3.53223661, 2.71900952],
[3.80569251, 2.92950765],
[5.57926356, 4.29474931],
[3.93851354, 3.03174929],
[6.94105849, 5.3430181 ],
[4.93142811, 3.79606507],
[5.58255993, 4.29728676],
[5.48117436, 4.21924319],
[5.38482148, 4.14507365],
[5.02696267, 3.8696047 ],
[5.54606249, 4.26919213],
[3.60199795, 2.77270971],
[6.58954104, 5.07243054],
[5.681006 , 4.37306758],
[4.02614513, 3.09920545],
[6.76785875, 5.20969415],
[5.50019161, 4.2338821 ],
[6.81311151, 5.24452836],
[4.56923815, 3.51726213],
[6.49947125, 5.00309752],
[4.94381398, 3.80559934],
[3.47034372, 2.67136624],
[4.41334883, 3.39726321],
[5.97375815, 4.59841938],
[6.10672889, 4.70077626],
[4.09805306, 3.15455801],
[4.90719483, 3.77741101],
[4.94773778, 3.80861976],
[6.36085631, 4.8963959 ],
[3.81339161, 2.93543419],
[5.61026298, 4.31861173],
[4.32622924, 3.33020118],
[6.02248932, 4.63593118],
[3.48356381, 2.68154267],
[6.19898705, 4.77179382],
[2.69816733, 2.07696807],
[5.18471099, 3.99103461],
[5.68860316, 4.37891565],
[4.14095516, 3.18758276],
[3.82801958, 2.94669436],
[5.73637229, 4.41568689],
[3.45624014, 2.66050973],
[5.10784454, 3.93186513],
[2.13253865, 1.64156413],
[3.65610482, 2.81435955],
[4.66128664, 3.58811828],
[6.1549641 , 4.73790627]])
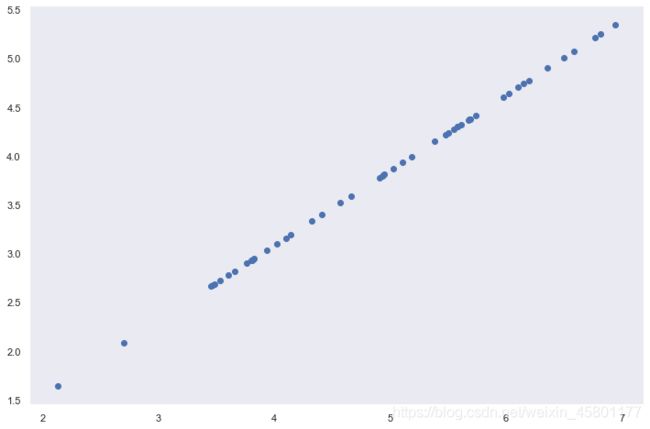
fig,ax = plt.subplots(figsize=(12,8))
ax.scatter(list(X_recovered[:,0]),list(X_recovered[:,1]))
plt.show()
图像降维
和之前的K-Means聚类类似,我们使用PCA降维,将颜色看做特征,导入共有32$\times$32个特征的图像,并提取前100个观察变化
faces = loadmat('ex7faces.mat')
X = faces['X']
X.shape
(5000, 1024)
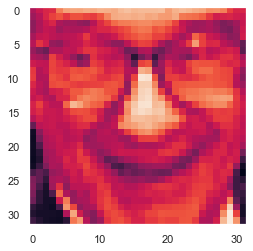
face = np.reshape(X[0,:],(32,32))
plt.imshow(face.T)
plt.show()
U,S,V = PCA(X)
Z = project_data(X,U,100)
X_recovered = recover_data(Z, U, 100)
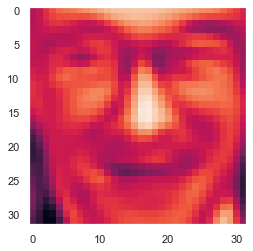
face = np.reshape(X_recovered[0,:], (32, 32))
plt.imshow(face.T)
plt.show()
我们可以发现很多细节被丢失因为只选取了100个主要特征。