【Asymmetric Tri-training for Unsupervised Domain Adaptation 2017 ICML】

Asymmetric Tri-training for Unsupervised Domain Adaptation

速览

背景及方法

  深层模型需要大量的标注样本进行训练，但是收集不同领域的标注样本是代价昂贵的。
  无监督领域自适应：利用标注的有标注的源样本和目标样本训练一个在目标域上能够很好地work的分类器。
存在的问题虽然很多的方法去对齐源域和目标域样本的分布，但是简单地匹配分布不能确保目标域上的准确率。
为了学习目标域的判别性的表示，假设人工标记的目标样本可以得到很好的表示。
Tri-training平等利用三个分类器提供无标记样本的伪标签，但该方法不假设标记来自不同领域的样本。

• Tri-training leverages three classifiers equally to give pseudo-labels to unlabeled samples, but the method does not assume labeling samples generated from a different domain.
  Proposed Method: asymmetric tri-training method for unsupervised domain adaptation
    为未标记的样本分配伪标签，并将其作为真实标签来训练神经网络。
    使用三个非对称网络。非对称，是使用两个网络来标记未标记的目标样本，一个网络被样本训练以获得目标判别性表示。

模型概览

根据在源样本上训练的两个分类器的预测，为未标记的目标样本分配伪标签。

方法包括一个共享特征提取器(F)、标记样本的分类器($F_1$、$F_2$)，从标记的源样本和新标记的目标样本中学习。此外，目标特异性分类器($F_t$)从伪标记的目标样本中进行学习。方法首先只从标记的源样本中训练网络，然后根据$F_1$、$F_2$的输出对目标样本进行标记。使用它们来训练所有的架构，就好像它们是正确标记的样本一样。

结果观察

数字和交通标志数据集上的视觉域自适应实验结果可视化

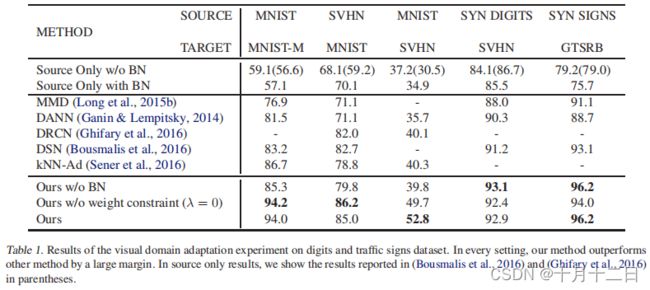
特征表示可视化(结合准确率(52.8%)理解)

训练期间伪标签的实际准确性和学习网络的准确性的比较。蓝色曲线是伪标签的准确性，红色曲线是学习网络的准确性。请注意，标签准确率是用（正确标注的样本数）/（标注的样本数）计算的。绿色曲线是每一步中标记的目标样本的数量。(f): 模型中三个网络的准确性比较。三个网络几乎同时提高了准确性。(g): 不同方法的A-distance的比较。模型与纯源训练的CNN相比，稍微减少了领域的分歧。

总结

Conclusion: 通过利用分配给未标记的目标样本的伪标签来学习鉴别性的表征。利用了三个分类器，其中两个网络为未标记的目标样本分配了伪标签，其余的网络则从这些伪标签中学习。

Introduction

Deep neural networks: 神经网络的一个问题是，尽管它们在从与训练样本相同的分布中产生的样本上表现良好，但在测试时，它们可能发现很难正确识别来自不同分布的样本。其中一个例子是从互联网上收集到的图像，它们可能会大量出现并被完全标记出来。它们的分布方式不同于用相机拍摄的图像。因此，一个在不同领域上表现良好的分类器对于实际应用是很重要的。为了实现这一点，有必要学习领域不变的判别表示。然而，获取这样的表示并不容易，因为通常 很难收集大量的标记样本，而且来自不同领域的样本具有特定领域的特征。

Unsupervised domain adaptation: 在训练时提供标记源样本和未标记目标样本的条件下，尝试训练一个在目标域上工作良好的分类器。以往的深度域自适应方法主要是在通过匹配不同域的特征分布来实现自适应的前提下提出的。这些方法旨在通过最小化域间的散度以及源域上的类别损失来获得域不变特征。然而，如(Ben-David et al.，2010)所示，从理论上讲，如果在源域和目标域都很有效的分类器不存在，不能期望目标域有判别分类器。也就是说，即使分布在非判别性表示上是匹配的，分类器可能在目标域上无法良好工作。由于在没有目标标签的情况下，直接学习目标领域的判别性表征被认为是非常困难的，建议给目标样本分配伪标签，并训练目标特定网络，就像它们是真正的标签一样。
   Co-training and tri-training(Zhou&Li，2005)利用多个分类器人为地标记未标记的样本，并对分类器进行再训练。然而，这些方法并不假设标记来自不同领域的样本（困惑）。由于本文目标是对与标记源样本具有不同特征的未标记目标样本进行分类，因此提出了非监督域自适应的非对称三训练。非对称，是指给三个分类器分配不同的角色。
  在本文中，提出了一种新的无监督域自适应的tri-training方法，其中将伪标记分配给未标记的样本，并利用这些样本训练神经网络。如图1所示，使用两个网络对未标记的目标样本进行标记，剩余的网络由伪标记的目标样本进行训练。方法不需要任何特殊的实现。使用Arazon评论数据集在数字分类任务、交通标志分类任务和情绪分析任务上评估了方法，并在几乎所有的实验中展示了最先进的性能。特别是在适应场景MNIST→SVHN中，方法比其他方法好10%以上。

Related Work

   以往的许多方法都试图通过测量不同领域之间的散度来实现自适应。这些方法基于(Ben-David et al.，2010)中提出的理论，该理论指出，目标域的期望损失以三项为界：(i)源域的期望损失；(ii)源和目标之间的域差异；(iii)共享的期望损失的最小值。共享的期望损失是指在源域和目标域上的损失之和。由于第三项，通常被认为是非常低的，当没有标记的目标样本时，不能进行评估，(假设第三项是非常小的)，大多数方法试图最小化第一项和第二项。在深度架构的训练中，利用最大平均差异(MMD)或域分类器网络的损失来度量与第二项对应的散度。
   然而， 第三项在训练CNN时非常重要，它同时提取表示和识别它们。当表示对目标域没有区别时，第三项很容易就会很大。因此，本文专注于如何在考虑第三项的情况下学习目标鉴别性表征。在 (Long et al., 2016)中，重点是前面所说的那一点，并且使用残差网络结构构建了一个目标特定的分类器。与他们的方法不同的是，本文通过提供人工标记的目标样本来构建一个目标特定( target-specific)的网络。
   有几种转换方法利用特征的相似性来为未标记的样品提供标签对于无监督域自适应，在(Sener et al., 2016)中，提出了一种通过使用未标记目标样本和标记源样本之间的k-最近邻来学习标记度量的方法。与此方法相比，本文的方法基于伪标记样本，明确而简单地反向传播了目标样本的类别损失。本文的方法不需要任何特殊的模块。
   许多方法提出，通过利用分类器的预测和包括伪标签样本在内的再训练，给无标签的样本提供伪标签，这被称为自训练( self-training)。自训练的基本假设是，其自己的高可信度预测是正确的(Zhu，2005)。由于预测大多是正确的，利用具有高可信度的样本将进一步提高分类器的性能。==协同训练(co-training)==利用两个在一个样本上有不同视图的分类器来提供伪标签。然后，如果至少有一个分类器对预测是可信的，则将未标记的样本添加到训练集中。在(Chen et al.，2011)中，协同训练的想法被纳入了领域适应。Tri-training可以被视为共同训练的延伸。与共同训练类似，Tri-training使用三种不同分类器的输出来给未标记的样本提供伪标签。Tri-training不需要将特征划分为不同的视图；相反，其以不同的方式初始化每个分类器。但是， Tri-training不假设未标记样本遵循与标记样本生成的不同分布。因此，本文开发了一种适合于使用三个非对称分类器的域自适应的Tri-training方法。
   在(Lee，2013)中，研究了伪标签在神经网络中的影响。他们认为，用伪标签训练一个分类器的效果等同于熵正则化，从而导致了类之间的低密度分离。此外，本文在实验中，观察到目标样本在隐藏的特征中被分离。

Method

   在本节中，提供所提出的领域自适应模型的细节。本文目标是利用伪标记的目标样本来构建一个目标特异性网络。同时，期望两个标记网络获得目标判别性的表示，并逐步提高目标域的精度。
   图2所示为所提出的网络结构。这里$F$表示输出三个网络之间共享特征的网络，$F_1$、$F_2$对$F$生成的特征进行分类，利用它们的预测给出伪标签。分类器$F_t$对由$F$生成的特征进行分类，是一个特定于目标的网络。这里$F_1$、$F_2$从源和伪标记目标样本中学习，$F_t$只从伪标记目标样本中学习。共享网络$F$从$F_1$、$F_2$、$F_t$的所有梯度中学习。如果没有这样的共享网络，可以想到的网络架构的另一个选择是分别训练三个网络，但这在训练和实现方面是低效的。此外，通过构建一个共享网络，$F$，$F_1$和$F_2$也可以利用从$F_t$反馈学习到的目标识别表征。源样本的集合被定义为${\left\{\left(x_i,y_i\right)\right\}}_{i=1}^{m_s}\sim \mathcal{S}$，未标记的目标集为${\left\{\left(x_i\right)\right\}}_{i=1}^{m_t}\sim \mathcal{T}$，而伪标记的目标集是${\left\{\left(x_i,{\hat{y}}_i\right)\right\}}_{i=1}^{n_t}\sim {\mathcal{T}}_l$。

Loss for Multiview Features Network

F1和F2的学习
  在现有的关于领域适应的协同训练的工作(Chen et al.，2011)中，给定的特征被划分为不同的部分，并被认为是不同的视图(views)。
  由于本文的目标是高精度地标记目标样本，期望$F_1$，$F_2$根据不同的角度( viewpoints)对样本进行分类。因此，对$F_1$、$F_2$的权重进行了一个约束，使它们的输入相互不同。将术语$|{W_1}^T{W}_2|$添加到代价函数中，其中$W_1$，$W_2$表示完全连接层的$F_1$和$F_2$的权重，首先应用于特征$F(x_i)$。在这个约束条件下，每个网络都将从不同的特性中学习。学习$F_1$，$F_2$的目标定义为：

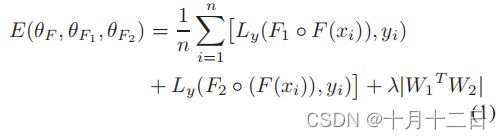
其中，$L_y$为标准的softmax交叉熵损失函数。基于验证分割决定了权衡参数$\lambda$.

Learning Procedure and Labeling Method

  伪标记的目标样本将为网络提供目标鉴别信息。然而，由于它们肯定包含错误的标签，必须选择可靠的伪标签。本文的标签/标注和学习方法就是为了实现这一点。
网络训练过程：

  首先，用源训练集$\mathcal{S}$训练整个网络。这里的$F_1$，$F_2$由等式(1)进行优化，$F_t$使用标准分类损失的训练。在$\mathcal{S}$上训练后，为了提供伪标签，使用$F_1$和$F_2$的预测，即从$x_k$得到的$y^1$，$y^2$。当$C_1$，$C_2$表示$y^1$，$y^2$的预测概率最大的类时，如果满足以下两个条件，为$x_k$分配一个伪标签。

1. 首先，要求$C_1=C_2$给出伪标签，这意味着两种不同的分类器与预测一致。
2. 其次，$y^1$或$y^2$的最大概率超过阈值参数，在实验中将其设为0.9或0.95。

  假设，除非两个分类器中的一个对预测有信心，否则预测是不可靠的。如果满足这两个要求，则将$\left(x_k,{\hat{y}}_k=C_1=C_2\right)$添加到${\mathcal{T}}_l$中。为了防止对伪标签的过拟合，在每个步骤中重新取样以标记候选样本。最初的候选的样本数$N_{init}$为5000。逐渐增加候选样本的数量$N_t=k/20\ast n$，其中$n$表示所有目标样本的数量，$k$表示步数，将伪标记候选样本的最大数量设置为40,000。在组成伪标记训练集${\mathcal{T}}_l$后，在标记的训练集$L=S\cup$${\mathcal{T}}_l$上由目标等式(1)更新$F、F_1、F_2$。然后，$F，F_t$被简单地通过${\mathcal{T}}_l$的类别损失进行优化。

  判别性的表示将通过构建一个仅针对目标样本进行训练的目标特定网络来学习。然而，如果只使用有噪声的伪标记样本进行训练，网络可能无法学习到有用的表示。但是，本文同时使用源样本和伪标记样本来训练$F、F_1、F_2$，以保证准确性。同时，随着学习过程的进行，F将学习目标判别表征，从而提高$F_1$、$F_2$的准确性。这个循环将逐渐提高目标域的精度。

Batch Normalization for Domain Adaptation

  批处理归一化(BN)(IOffe&Szegedy，2015)，它减少了CNN中隐藏层的输出，是一种加快训练速度、提高模型精度的有效技术。此外，在领域自适应中，白化隐藏层的输出可以有效地提高性能，使不同领域的分布相似(Sun et al.，2016；Lietal.，2016)。$F_1、F_2$的输入样本包括伪标记的目标样本和源样本。引入BN将有助于匹配分布和提高性能。在$F$的最后一层中添加BN层。

Analysis

  将对方法进行理论分析。首先，提供了一个对现有理论的见解，然后介绍一个与本文的方法相关的简单的扩展的理论。
  在(Ben-David et al.，2010)中，引入了一个方程，表明目标域的期望误差的上界取决于三项，其中包括不同域之间的散度和理想联合假设的误差。
  源域与目标域之间的散度，$\mathcal{H}\Delta \mathcal{H}\text{-distance }$，定义如下：

这个距离经常被用来衡量不同域之间的适应性。
  理想联合假设定义：

  Ben-David理论定义：

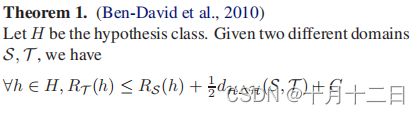
  该定理意味着目标域上的期望误差上限有三项、源域上的期望误差、由假设不一致测得的域散度以及理想联合假设的误差。在现有的工作中，理想联合假设误差$C$被忽略了，因为它被认为是可以忽略不计的小。如果提供了固定的特性，不需要考虑这个项，因为这个项也是固定的。
  但是，如果假设$x_s\sim S，x_t\sim T$是从深度模型的最后一个全连接层获得的，注意到$C$是由该层的输出决定的，并进一步注意考虑这个项的必要性。考虑伪标记的目标样本集${\left\{\left(x_i,{\hat{y}}_i\right)\right\}}_{i=1}^{n_t}\sim {\mathcal{T}}_l$在$\rho$的比例下给出了假标签。$h^{\ast }$对$S$，${\mathcal{T}}_l$的共享误差记为$C’$。那么，以下的不等式成立：

  在补充材料中给出了该不等式的一个简单推导。在定理1中，不能在没有标记的目标样本的情况下测量$C$。可以通过使用伪标签来近似地计算和最小化它。此外，当考虑右边的第二项时，本文的方法有望减少这个项。这个项直观地表示两个分类器在不同域之间的差异。如果将特定的$h$和$h‘$分别视为$F_1$和$F_2$，那么$\underset{\mathbf{x}\sim {\mathcal{S}}_{\mathbf{x}}}{E}\left[h(\mathbf{x})\ne h^{\prime }(\mathbf{x})\right]$应该非常低，因为训练是基于相同的标记样本。此外，出于同样的原因，$\underset{\mathbf{x}\sim {\mathcal{T}}_{\mathbf{x}}}{E}\left[h(\mathbf{x})\ne h^{\prime }(\mathbf{x})\right]$预计较低，虽然使用训练集${\mathcal{T}}_l$而不是真正的标记目标样本。因此，本文的方法将同时考虑定理1中的第二项和第三项。

Experiment and Evaluation

  在图像数据集和情绪分析数据集上对的方法进行了广泛的评估。在所有实验中评估了目标特定网络的准确性。
Visual Domain Adaptation： 对于视觉域自适应，对数字数据集和交通标志数据集进行评估。本实验共评估了五种适应情景。
  本文没有在Office上评估方法，这是视觉领域自适应最常用的数据集。正如(Bousmalis et al.，2016)所指出的，该数据集中的一些标签是有噪声的，而一些图像包含其他类的对象。此外，许多以前的研究已经评估了使用ImageNet对预训练网络的微调。该协议假设存在另一个源域。在本文的工作中，希望评估只能访问一个源域和一个目标域的情况。
Adaptation in Amazon Reviews： 为了调查语言数据集上的行为，在亚马逊评论数据集上评估了方法，其预处理方法与y (Chen et al., 2011;Ganin et al., 2016)相同。该数据集包含了对四种类型的产品的评论：书籍、DVD、电子产品和厨房电器。在12个领域的自适应场景中评估了方法。结果如表1所示。
Baseline Methods： 与进行无监督领域适应的五种方法进行比较，包括视觉领域适应的最新方法。

Implementation Detail

  在图像数据集上的实验中，采用了在(Ganin&Lempitsky，2014)中使用的CNN架构。为了进行公平的比较，本文在隐藏层分离了网络(Ganin&Lempitsky，2014)构建了鉴别网络。因此，当考虑一个分类器时，例如$F_1◦F$，其体系结构与之前的工作是相同的。也遵循了其他协议中的规定(Ganin&Lempitsky，2014)。在MNIST→SVHN中设置标记方法的阈值为0.95。在其他场景下，将其设置为0.9。使用MomentumSGD进行优化，并将动量设置为0.9，而学习率是由验证分割决定的，并使用了[0.01,0.05]。$\lambda$在所有场景中都被设置为0.01。在补充材料中，提供了网络架构和超参数的细节。
  对于亚马逊评论数据集上的实验，使用了与(Ganin et al.，2016)中类似的架构：with sigmoid activated, one dense hidden layer with 50 hidden units, and softmax output。在CNN的架构中扩展到本文的方法。根据验证，$\lambda$设置为0.001。由于输入是稀疏的，使用Adagrad(Duchi et al.，2011)进行优化。重复这个评估10次，并报告平均准确性。

Experimental Result

  在表1和表3中，展示了实验的主要结果。当只对源样本进行训练时，BN的影响并不清晰，如表1所示。然而，在所有的图像识别实验中，BN在本文的方法中的影响是明显的；同时，当本文在网络架构中不使用BN时，本文的方法的效果也很明显。权重约束的影响在MNIST→SVHN中是明显的。

MNIST→MNIST-M首先，评估手写数字数据集MNIST与其转换后的数据集MNIST-M之间的自适应场景。MNIST-M是通过合并来自BSDS500数据集的背景剪辑而组成的(Arbelaez et al.，2011)。从BSDS500中的图像中随机抽取一个补丁，并合并为MNIST个数字。即使有这种简单的域漂移，CNN的适应性能比在目标样本上训练的情况要差得多。从59,001个目标训练样本中，随机选择了1,000个标记的目标样本作为验证分割和调整的超参数。本文的方法比现有的其他方法高出约7%。最后一个池化层的特征可视化如图3(a)(b).所示可以观察到，当实现自适应时，红色的目标样本更加分散。本文在图4中比较了训练时对目标样本的实际标记精度与测试精度之间的精度。测试精度起初很低，但随着步数的增加，测试精度越来越接近标记精度。在这种适应中，可以清楚地看到，随着网络的精度，实际标记精度逐渐提高。
SVHN↔MNIST在这个实验中，增加了分布之间的差距。评估了SVHN(Netzer et al.，2011)和MNIST在一个十类分类问题中的适应性。SVHN和MNIST有明显的外观，因此这种适应是一个具有挑战性的场景，特别是在MNIST→SVHN。SVHN是彩色的，一些图像包含多个数字。因此，在SVHN上训练的分类器有望在MNIST上表现良好，但事实恰恰相反。MNIST不包括任何包含多位数字的样本，而大多数样本都是以图像为中心，因此从MNIST到SVHN的适应是相当困难的。在这两种情况下，都使用1000个标记的目标样本来找到最优的超参数。

  在两种自适应场景上评估了方法，并在两个数据集上取得了最先进的性能。特别是，对于自适应MNIST→SVHN，比其他方法好了10%以上。在图3©(d)中，可视化了MNIST→SVHN中的表示。虽然分布似乎在域之间是分开的，但与非适应嵌入相比，本文的方法使红色SVHN样本变得更具区别性。还在图4(b) ( c )。中显示了实际标记方法的精度和测试精度之间的比较。在这个图中，可以看到，标记精度在初始适应阶段迅速下降。另一方面，测试精度不断提高，最终超过了标记精度。关于这个有趣的现象，有两个问题。第一个问题是，为什么尽管测试精度提高，但标记方法继续下降？给定伪标签的目标样本总是包含错误标记的样本，而那些没有标记的样本在本文的方法中被忽略。因此，该误差将在训练集中所包含的目标样本中得到加强。第二个问题是，为什么尽管标签精度较低，但测试的准确性会继续提高？假设的原因是网络在这个阶段已经获得了目标的鉴别表示，它们可以提高使用源样本和正确标记目标样本的精度。
   在图4(f)中，还展示了SVHN→MNIST中三个网络$F_1、F_2、F_t$的精度比较。三个网络的精度在每一步中几乎是相同的。在其他情况中也可以观察到同样的情况。从这个结果中，可以声明，目标区分表示在所有三个网络中都是共享的。

时间关系，其余实验结果暂略

论文链接