最小二乘法 python实现
最小二乘法适用于对处理的一堆数据,不必精确的经过每一点,而是根据图像到每个数据点的距离和最小确定函数。
最小二乘法逼近的最简单的例子是根据一组观测值对(x1,y1),(x2,y2)…(xn,yn)来拟合一条直线。直线的数学表达式为

下面是一元线性拟合的原理说明:

一元线性拟合的python实现代码
import matplotlib.pyplot as plt
from pylab import mpl
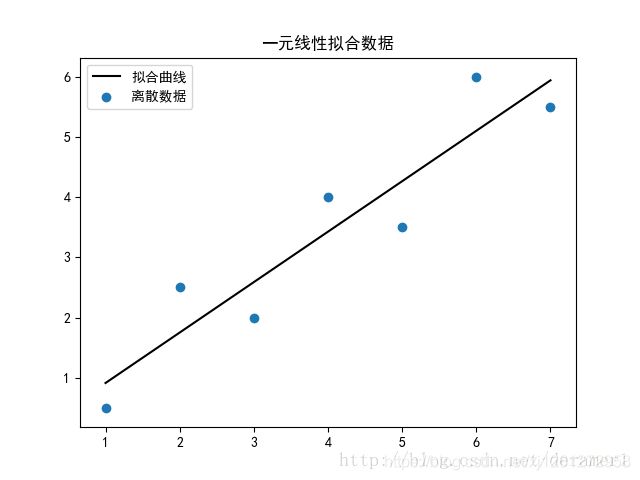
"""一元线性拟合
采用的拟合数据为xi=1,2,3,4,5,6,7
对应的相应函数值yi=0.5,2.5,2,4,3.5,6,5.5
"""
x = [1, 2, 3, 4, 5, 6, 7];
y = [0.5, 2.5, 2, 4, 3.5, 6, 5.5]
"""完成拟合曲线参数计算"""
def liner_fitting(data_x,data_y):
size = len(data_x);
i=0
sum_xy=0
sum_y=0
sum_x=0
sum_sqare_x=0
average_x=0;
average_y=0;
while i<size:
sum_xy+=data_x[i]*data_y[i];
sum_y+=data_y[i]
sum_x+=data_x[i]
sum_sqare_x+=data_x[i]*data_x[i]
i+=1
average_x=sum_x/size
average_y=sum_y/size
return_k=(size*sum_xy-sum_x*sum_y)/(size*sum_sqare_x-sum_x*sum_x)
return_b=average_y-average_x*return_k
return [return_k,return_b]
"""完成完后曲线上相应的函数值的计算"""
def calculate(data_x,k,b):
datay=[]
for x in data_x:
datay.append(k*x+b)
return datay
"""完成函数的绘制"""
def draw(data_x,data_y_new,data_y_old):
plt.plot(data_x,data_y_new,label="拟合曲线",color="black")
plt.scatter(data_x,data_y_old,label="离散数据")
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.title("一元线性拟合数据")
plt.legend(loc="upper left")
plt.show()
parameter = liner_fitting(x,y)
draw_data = calculate(x,parameter[0],parameter[1])
draw(x,draw_data,y)
一元多项式拟合
有的时候,给出的变量关系不是直线的关系,而是曲线的关系,这个时候需要我们用多项式来进行拟合。

下面是一元多项式拟合的python实现
import matplotlib.pyplot as plt
from pylab import mpl
import math
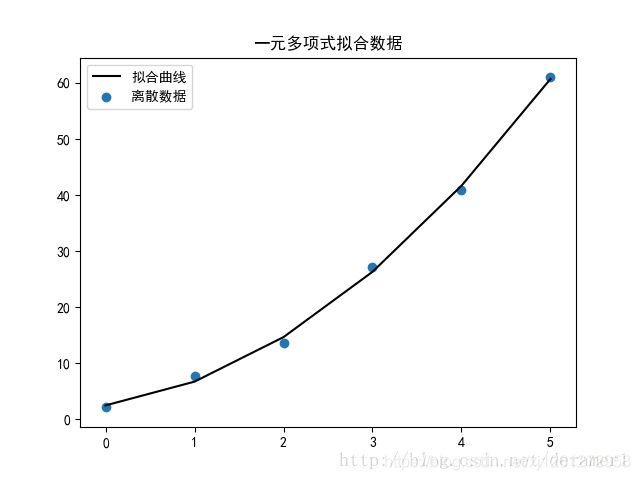
"""一元多项式曲线拟合
拟合数据为xi=0, 1, 2, 3, 4, 5
对应的函数值yi=2.1, 7.7, 13.6, 27.2, 40.9, 61
"""
x = [0, 1, 2, 3, 4, 5]
y = [2.1, 7.7, 13.6, 27.2, 40.9, 61]
"""完成拟合曲线参数计算前相应变量的计算"""
def polynomial_fitting(data_x,data_y):
size=len(data_x)
i=0
sum_x = 0
sum_sqare_x =0
sum_third_power_x = 0
sum_four_power_x = 0
average_x = 0
average_y = 0
sum_y = 0
sum_xy = 0
sum_sqare_xy = 0
while i<size:
sum_x += data_x[i]
sum_y += data_y[i]
sum_sqare_x += math.pow(data_x[i],2)
sum_third_power_x +=math.pow(data_x[i],3)
sum_four_power_x +=math.pow(data_x[i],4)
sum_xy +=data_x[i]*data_y[i]
sum_sqare_xy +=math.pow(data_x[i],2)*data_y[i]
i += 1;
average_x=sum_x/size
average_y=sum_y/size
return [[size, sum_x, sum_sqare_x, sum_y]
, [sum_x, sum_sqare_x, sum_third_power_x, sum_xy]
, [sum_sqare_x,sum_third_power_x,sum_four_power_x,sum_sqare_xy]]
"""完成拟合曲线参数的计算
其中解方程的时候,利用高斯消元法计算相应的参数值
"""
def calculate_parameter(data):
#i用来控制列元素,line是一行元素,j用来控制循环次数,datas用来存储局部变量。保存修改后的值
i = 0;
j = 0;
line_size = len(data)
#将行列式变换为上三角行列式
while j < line_size-1:
line = data[j]
temp = line[j]
templete=[]
for x in line:
x=x/temp
templete.append(x)
data[j]=templete
#flag标志应该进行消元的行数
flag = j+1
while flag < line_size:
templete1 = []
temp1=data[flag][j]
i = 0
for x1 in data[flag]:
if x1!=0:
x1 = x1-(temp1*templete[i])
templete1.append(x1)
else:
templete1.append(0)
i += 1
data[flag] = templete1
flag +=1
j += 1
#求相应的参数值
parameters=[]
i=line_size-1
#j标识减去元素个数
#flag_rol标识除那一列
flag_j=0
rol_size=len(data[0])
flag_rol=rol_size-2
#获得解的个数
while i>=0:
operate_line = data[i]
if i==line_size-1:
parameter=operate_line[rol_size-1]/operate_line[flag_rol]
parameters.append(parameter)
else:
flag_j=(rol_size-flag_rol-2)
temp2=operate_line[rol_size-1]
#result_flag为访问已求出解的标志
result_flag=0
while flag_j>0:
temp2-=operate_line[flag_rol+flag_j]*parameters[result_flag]
result_flag+=1
flag_j-=1
parameter=temp2/operate_line[flag_rol]
parameters.append(parameter)
flag_rol-=1
i-=1
return parameters
"""计算拟合曲线的值"""
def calculate(data_x,parameters):
datay=[]
for x in data_x:
datay.append(parameters[2]+parameters[1]*x+parameters[0]*x*x)
return datay
"""完成函数的绘制"""
def draw(data_x,data_y_new,data_y_old):
plt.plot(data_x,data_y_new,label="拟合曲线",color="black")
plt.scatter(data_x,data_y_old,label="离散数据")
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.title("一元多项式拟合数据")
plt.legend(loc="upper left")
plt.show()
data=polynomial_fitting(x,y)
parameters=calculate_parameter(data)
for w in parameters:
print(w)
newData=calculate(x,parameters)
draw(x,newData,y)
有的时候,影响y的因素不止一个,而是多个因素,这个时候就需要多元线性拟合。
下面的python程序是两变量的线性拟合,还有最后图像的显示。
from mpl_toolkits.mplot3d import Axes3D
from pylab import mpl
import math
import matplotlib.pyplot as plt
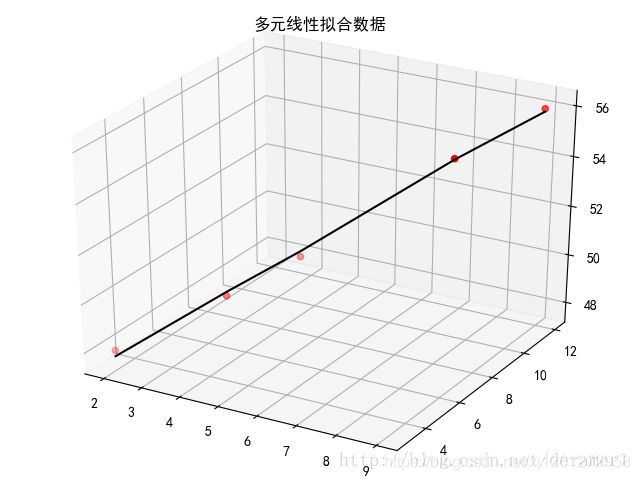
"""多元线性拟合
其中拟合数据为x1=2, 4, 5, 8, 9
x2=3, 5, 7, 9, 12
y=48, 50, 51, 55, 56
"""
x1 = [2, 4, 5, 8, 9]
x2 = [3, 5, 7, 9, 12]
y = [48, 50, 51, 55, 56]
"""完成拟合曲线参数计算前相应变量的计算"""
def multivariatel_liner_fitting(data_x1,data_x2,data_y):
size = len(data_x1)
sum_x1 = 0
sum_x2 = 0
sum_square_x1 = 0
sum_square_x2 = 0
sum_x1x2 = 0
sum_y = 0
sum_x1y = 0
sum_x2y = 0
i = 0
while i < size:
sum_x1 += data_x1[i]
sum_x2 += data_x2[i]
sum_y += data_y[i]
sum_x1y += data_x1[i]*data_y[i]
sum_x2y += data_x2[i]*data_y[i]
sum_x1x2 += data_x1[i]*data_x2[i]
sum_square_x1 += data_x1[i]*data_x1[i]
sum_square_x2 += data_x2[i]*data_x2[i]
i += 1
return [[size, sum_x1, sum_x2, sum_y]
,[sum_x1, sum_square_x1, sum_x1x2, sum_x1y]
,[sum_x2, sum_x1x2, sum_square_x2,sum_x2y]]
"""利用高斯消元法,求解拟合曲线的参数"""
def calculate_parameter(data):
#i用来控制列元素,line是一行元素,j用来控制循环次数,datas用来存储局部变量。保存修改后的值
i = 0;
j = 0;
line_size = len(data)
#将行列式变换为上三角行列式
while j < line_size-1:
line = data[j]
temp = line[j]
templete=[]
for x in line:
x=x/temp
templete.append(x)
data[j]=templete
#flag标志应该进行消元的行数
flag = j+1
while flag < line_size:
templete1 = []
temp1=data[flag][j]
i = 0
for x1 in data[flag]:
if x1!=0:
x1 = x1-(temp1*templete[i])
templete1.append(x1)
else:
templete1.append(0)
i += 1
data[flag] = templete1
flag +=1
j += 1
#求相应的参数值
parameters=[]
i=line_size-1
#j标识减去元素个数
#flag_rol标识除那一列
flag_j=0
rol_size=len(data[0])
flag_rol=rol_size-2
#获得解的个数
while i>=0:
operate_line = data[i]
if i==line_size-1:
parameter=operate_line[rol_size-1]/operate_line[flag_rol]
parameters.append(parameter)
else:
flag_j=(rol_size-flag_rol-2)
temp2=operate_line[rol_size-1]
#result_flag为访问已求出解的标志
result_flag=0
while flag_j>0:
temp2-=operate_line[flag_rol+flag_j]*parameters[result_flag]
result_flag+=1
flag_j-=1
parameter=temp2/operate_line[flag_rol]
parameters.append(parameter)
flag_rol-=1
i-=1
return parameters
def calculate(data_x1,data_x2,parameters):
datay=[]
i = 0
while i < len(data_x1):
result = parameters[2]+parameters[1]*data_x1[i]+parameters[0]*data_x2[i]
i += 1
datay.append(result)
return datay
"""完成函数的绘制"""
def draw(data_x,old_y,new_y):
#创建绘图函数对象
fig = plt.figure()
#创建Axes3D对象,让其包含图像3D坐标
ax = Axes3D(fig)
ax.scatter(data_x[0], data_x[1], old_y, color='red')
ax.plot(data_x[0], data_x[1], new_y, color='black')
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.title("多元线性拟合数据")
plt.show()
data = multivariatel_liner_fitting(x1, x2, y)
data2 = calculate_parameter(data)
newY = calculate(x1, x2, data2)
draw([x1, x2], y, newY)