MATLAB--列文伯格LM优化算法

1.LM函数定义

输入参数：误差函数，需要优化的形参，初值

function last_parameters = LM(fr,p_sym,parameters)
% jacobin matrix
Jr = jacobian(fr,p_sym);
% loss function
F = 0.5*fr'*fr;

para = {};
para_new = {};
for i=1:size(p_sym,1)
    para{i} = parameters(i);
end

%set the inital values
k=0;
v=2;
k_max = 1000;
tao=1e-12;
miu = vpa(tao*max(diag(Jr(para{:})'*Jr(para{:}))),10);

A = Jr(para{:})'*Jr(para{:});
g = Jr(para{:})'*fr(para{:});

% set the state of found
found = (norm(g)<1e-12);

while(~found && k<k_max)
    k=k+1;
    h_lm = -(A+miu*eye(size(p_sym,1)))\g;
    if(norm(h_lm)<= 1e-12*(norm(parameters)+1e-12))
        found=true;
    else
        x_new = parameters + h_lm;
        for i=1:size(p_sym,1)
            para_new{i} = x_new(i);
        end
        
        Fx = F(para{:});
        Fxnew = F(para_new{:});
        
        Jrx0 = Jr(para{:});
        frx0 = fr(para{:});
        %L0-Lh = 0.5*h_lm'*(miu*h_lm-Jrx0'*frx0)
        rho = (Fx-Fxnew)./(0.5*h_lm'*(miu*h_lm-Jrx0'*frx0));
        
        if rho>0
            parameters = x_new;
            for i=1:size(p_sym,1)
                para{i} = parameters(i);
            end
            A = Jr(para{:})'*Jr(para{:});
            A = vpa(A,10);
            g = Jr(para{:})'*fr(para{:});
            g = vpa(g,10);
            %reset the found
            found = (norm(g)<=1e-12);
            miu = miu*max([0.333,1-(2-rho)^3]);
            v = 2;
        else
            miu = miu*v;
            v = 2*v;
        end
    end
end

last_parameters = vpa(parameters,6);
end

2. 示例

clear all;
clc
%%演示LM法--非线性优化

%真实值
ar = 1.0;
br = 2.0;
cr = 1.0;
x = 1:2:100;
x = x./100;
nosie = 0.9*randn(1,size(x,2));%产生高斯噪音
y_real = exp(ar*x.^2+br*x+cr)+nosie;

%估计初始值
ae = 2.0;
be = 4.0;
ce = 3.0;
InitalValue = [ae;be;ce];


syms x_ a b c;
arg = [a;b;c];
f(a,b,c,x_) = exp(a*x_.^2+b*x_+c);

% 定义误差函数 Loss = y - f(x);
fr=[];
for i=1:size(x,2)
    f_(a,b,c) = y_real(i)-f(a,b,c,x(i));
    fr=[fr;f_];
end

last_result = LM(fr,arg,InitalValue);

plot(x,f(last_result(1),last_result(2),last_result(3),x));
hold on;
grid on;
scatter(x,y_real,100,'black','.');

3.示例2：相机参数优化

clear;
clc;
pw = [0,0,0;0,10,0;10,0,0;
    0,0,10;10,-10,0;-10,0,10;
    0,-10,0;-10,0,0;0,0,-10;
    -10,10,0;10,0,-10]';

pu = [540.0000,840,1;540,949.4322,1;
    690,840,1;540,747.0674,1;697.8947,719.0486,1;
    401.9550,747.0674,1;
    540,719.0486,1;
    390,840,1;
    540,950.5550,1;
    397.1429,949.4322,1;
    704.2220,950.5551,1;]';

syms fx fy Cx Cy Ax Ay Az Tx Ty Tz;
% K_sym
K_sym_d = [fx, 0, Cx;
            0, fy, Cy;
            0, 0, 1];
% T_sym
T_sym_d = [Tx;Ty;Tz];
% R_sym
R_sym_d = [cos(Ay)*cos(Az), -cos(Ay)*sin(Az),sin(Ay);
    sin(Ax)*sin(Ay)*cos(Az)+cos(Ax)*sin(Az),-sin(Ax)*sin(Ay)*sin(Az)+cos(Ax)*cos(Az),-sin(Ax)*cos(Ay);
    -cos(Ax)*sin(Ay)*cos(Az)+sin(Ax)*sin(Az),cos(Ax)*sin(Ay)*sin(Az)+sin(Ax)*cos(Az),cos(Ax)*cos(Ay)];

% all parameters
p_sym = [fx; fy; Cx; Cy; Ax; Ay; Az; Tx; Ty; Tz];

% initial values
fx_=1500; fy_=1500; Cx_=500; Cy_=500; 
Ax_=0; Ay_=0; Az_=0; Tx_=100; Ty_=100; Tz_=100;
InitalValue = [fx_; fy_; Cx_; Cy_; Ax_; Ay_; Az_; Tx_; Ty_; Tz_];

% error function
fr = [];
for i=1:size(pu,2)
    % Pc = T*Pw
    temporary = R_sym_d*pw(:,i)+T_sym_d;
    f_(fx,fy,Cx,Cy,Ax,Ay,Az,Tx,Ty,Tz) = pu(:,i) - 1/temporary(3)*K_sym_d*(R_sym_d*pw(:,i)+T_sym_d);
    fr = [f_;fr];
end

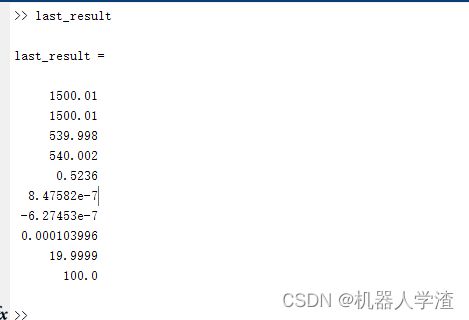
last_result = LM(fr,p_sym,InitalValue);