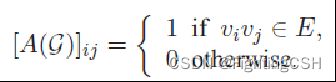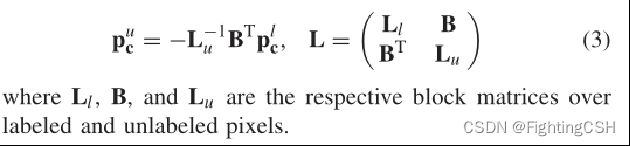Facet Kernel详解、Random Walk随机游走算法详解
之前在处理项目相关的红外小目标检测时，阅读到一片19年TGRS的文章：
Infrared Small Target Detection Based on Facet Kernel and Random Walker
其发表的FKRW算法流程为：
（1）预处理：统计滤波+均值滤波
（2）Facet Kernel + 阈值分割前背景：使用Facet Kernel 提取可能目标区域，在使用阈值分割
关键在于Facet kernel怎么来的，为什么如此涉及
（3）Random walker随机游走算法：使用RM算法，以类似ROI的思想与连通域的思想，对结果图进行分析，确定目标与背景杂音之间区别，并由此进行区分
（4）NLCD因子计算（目前先略，后续补充）
**************************************************************************************************************
首先，本文的PFT-saliency显著性方法是基于傅里叶变换的视觉显著性检测。
对视觉显著性建模的研究表明，自然图像的傅里叶变换相位谱（PFT）丰富地包含了引起人类注意的显著信号的位置信息
那么基于PFT的显著性如何度量？给出公式如下：
![p=P[F(I))]](http://img.e-com-net.com/image/info8/09a0b7bb4160428f8873fc69eda13010.gif){kind=small}
其中
&
分别代表Fouier与inverse Fouier变换，
代表相位谱计算，
代表高斯滤波，
代表最终的显著性图。
但研究显示，PFT-saliency会带来不希望出现的杂波，同时干扰红外小目标检测效果，造成检测失败的结果。
故，文章提出了一个新的快速显著性的方法
**************************************************************************************************************
Facet Kernel的来源以及其设计思路
Facet Kernel起源于Facet 模型
Facet模型包含一个假设：假设某像素的灰度强度曲面可用一个二元三次多项式近似。但使用最小二乘来逼近这个强度曲面，则会过于computationally intense。所以如果该强度曲面可以由一堆离散正交多项式线性组合而成，则计算起来会方便许多。总而言之，使用DOP（离散正交多项式）的线性组合就是为了简化计算，提升计算效率。
至于离散正交多项式的正交基与基前系数怎么求，具体的数学推导不便在文章中呈现。但这里给出思路：
（1）确定二维对称邻域大小R*C
（2）由于基底完全由二维对称邻域大小确定，且其中的系数完全由邻域坐标决定，所以近凭R*C邻域坐标即可确定出该邻域对应的基的具体情况。
（3）鉴于第二步已经精确求出R*C邻域的基底，则接下来需要确定用于拟合的离散正交基的基前系数K。由于要使用最小二乘法逼近原始图像的灰度曲面（![\varepsilon =[I(r,c)-f(r,c)]\textup{2}](http://img.e-com-net.com/image/info8/0d52e549505345e695ee636c8e7f92b8.gif){kind=small}
），通过数学推导后，可以直观发现，基前系数
即
也就是说，基前系数
可由以
为矩阵内量的矩阵与
邻域的
卷积表示。
简言之，只要知道
邻域大小与对应的图像灰度，便可以拟合出该邻域内的灰度曲面
以上便是Facet 模型的思想
接下来开始讲解基于Facet model的Facet kernel的由来：因为我们要突出小目标的位置，并将其与背景分开来，便可以与显著性思想联系起来。但由于频谱残差方法与PFT方法在小目标检测时，基本等效于高斯平滑与梯度计算。所以我们便可以通过求解图像patch的梯度来获得显著性图像，亦即，突出小目标。
既然要求梯度，就必然要获得图像的灰度分布曲面函数，但求解通过直接拟合函数逼近真实分布过于耗时，无法达到实时性的要求，于是便选用Facet model，通过一群离散切比雪夫多项式来逼近真实分布函数（思想类似于傅里叶变换逼近）。
通过上文中对Facet model的讲解，仅需要得知n*n大小的坐标与其中每个坐标对应的真实像素值，即可求解逼近二元三次灰度分布曲面的Facet model。
有了图像patch的分布函数：
(二元三次曲面的基只有10个)
由于我们不需要获取patch中每个像素的梯度（卷积核后滑会重复计算），所以只计算patch的中心像素梯度即可。对
求二阶偏导，便可获得patch中心像素梯度：
那么
如何获得
上面对Facet model的讲解中说到了，所有的基前系数均可用权重矩阵与patch卷积获得：
而权重矩阵又仅由patch坐标得来。所以
求解如下:
其中 
求梯度要进行两次卷积，但
结构相同，只是转置，所以用
去与patch卷积就好了。
那么便是我们的Facet Kernel：
简言之，使用Facet Kernel对图像卷积，便可得到图像梯度图，亦即，显著性图像。
**************************************************************************************************************
Random walker随机游走算法
由2006年的一片PAMI讲起：
Random walks for image segmentation. IEEE Transactions on Pattern Analysis & Machine Intelligence, 28, 1768-1783.
RW算法核心理念就是：任何随机行走者所携带的守恒量都各自遵循一个扩散规律。
从一个或一系列顶点开始遍历一张图。在任意一个顶点，遍历者将以概率1-a游走到这个顶点的邻居顶点，以概率a随机跳跃到图中的任何一个顶点，称a为跳转发生概率，每次游走后得出一个概率分布，该概率分布刻画了图中每一个顶点被访问到的概率。用这个概率分布作为下一次游走的输入并反复迭代这一过程。当满足一定前提条件时，这个概率分布会趋于收敛。收敛后，即可以得到一个平稳的概率分布。
首先，用一个一维情况先来解释RW算法：初始条件： 一维空间中，从左到右依次有点0~点W。从任意一个点（非点0与点W）出发，向左向右移动的概率均为1/2，到达边界之后停止移动。 用
代表初始位置为n最终到达边界点0的概率。
；
。由全概率公式有：
整理一下：
左右同减
:
......=
迭代相加得：
(解得 
)
最终解得：
概率趋于稳定。
二维情况，虽更复杂，但思维方式上与一维完全相同，最终到达固定seed的概率也会趋于稳定
其次，RW算法是一个基于图网的应用于图像分割的高效算法。既然基于图网，必须要给出图的精准定义：
（1）图结点：
（2）连接节点的边：
, 
代表该边连接结点
与
（3）边的权重：
= 
（4）结点的度：
,代表第i个结点的度=所有连接结点的边权重之和
（5）度矩阵：
.度矩阵代表每个结点的度，度表示每个顶点连接边的数量（权重之和）
(6) 邻接矩阵：
邻接矩阵。代表点与点之间的连接情况
(7) 拉普拉斯矩阵：
或引入权重后的
本文中拉普拉斯矩阵的定义如下：
边权重与图像结构的映射
由于RW算法是一个基于图网的算法，而我们处理的却是基于图像的问题。如何将图像与图网建立映射？答案便是使用图的边权重来代表图像结构，这也是使用图网来分析图像的常见方式。
在给定图网的精准定义后，第一件事就是如何确定边权重？
RW算法采用传统的高斯权重函数来度量边权重，公式如下：
其中，
与
分别代表图像
与
的像素强度，而
则是整个算法中唯一的可变系数。
且在定义权重前，将像素梯度
归一化一下，会很有用很方便后续处理。
如何解决上述“有限时间无法计算”的问题
上文说到，随机游走算法判断某一
属于哪一类时的方法是，判定该第一次到达某个种子节点时的概率。而由文献[1][2][3]文章作者由注意到，组合Dirichlet问题的解与期望的random walk概率相等。
[1] P. Doyle and L. Snell, Random Walks and Electric Networks, no. 22, Washington, D.C.: Math. Assoc. of Am., 1984
[2] S. Kakutani, “Markov Processes and the Dirichlet Problem,” Proc. Japanese Academy, vol. 21, pp. 227-233, 1945
[3] Grady, L. . (2006). Random walks for image segmentation. IEEE Transactions on Pattern Analysis & Machine Intelligence, 28, 1768-1783
最终解得,其中X为未标记点被分类为某一类的概率，
与
如下所示。
但作者用另一种方式给出了解：既然概率趋于稳定，在初始阶段，整个系统的能量必定是最高的，最终趋于稳定最小。 最小化能量函数：
如上所解，RW算法便可计算出每个未标记点的分类情况 。
RW算法解释完毕。如读者有什么问题，可随意在评论区留言。