神经网络反向传播算法(BP算法)
一、反向传播算法原理
反向传播算法概念:最初,所有的边权重(edge weight)都是随机分配的。对于所有训练数据集中的输入,人工神经网络都被激活,并且观察其输出。这些输出会和我们已知的、期望的输出进行比较,误差会「传播」回上一层。该误差会被标注,权重也会被相应的「调整」。该流程重复,直到输出误差低于制定的标准。
传播原理:反向传播主要依赖于链式法则复合函数求导
如下图, y是复合函数:
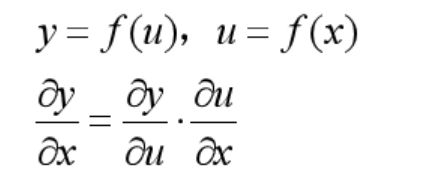
反向传播的优点:使用一次前向传播和一次反向传播,就同时计算出所有参数的偏导数。 反向传播计算量和前向传播差不多,并且有效利用前向传播过程中的计算结果,前向传播的主要计算的量在权重矩阵和input vector的乘法计算, 反向传播则主要是 矩阵和input vector 的转置的乘法计算。
二、BP算法推导过程
1、一个神经元
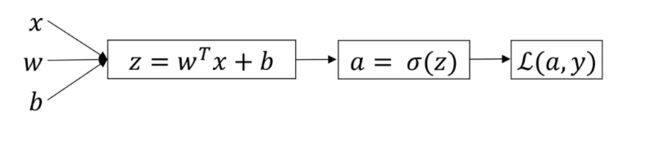
上图中表示一个神经元的正向传播,其中 a = σ ( z ) a=\sigma(z) a=σ(z)表示激活函数, L ( a , y ) L(a,y) L(a,y)表示损失函数(成本函数)。反向传播算法就是从 L ( a , y ) L(a,y) L(a,y)开始,一级一级的求出各个中间变量的导数,最终得到权重参数的导数,不断更新权重参数让输出值与真实值之间的误差越来越小。
如下图:
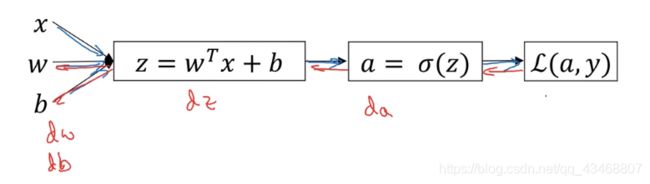
L ( a , y ) = − y log a − ( 1 − y ) log ( 1 − a ) L(a,y)=-y\log a - (1-y)\log (1-a) L(a,y)=−yloga−(1−y)log(1−a)
d a = d d a ⋅ L ( a , y ) 公 式 ( 1 ) da = \frac {d}{da}\cdot L(a,y)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~公式(1) da=dad⋅L(a,y) 公式(1)
= − y a + 1 − y 1 − a ~~~~~=-\frac{y}{a}+\frac{1-y}{1-a} =−ay+1−a1−y
d z = d L d a ⋅ d a d z 公 式 ( 2 ) dz = \frac{dL}{da}\cdot \frac{da}{dz}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~公式(2) dz=dadL⋅dzda 公式(2)
= ( − y a + 1 − y 1 − a ) ⋅ σ ′ ( z ) ~~~~~=(-\frac{y}{a}+\frac{1-y}{1-a})\cdot\sigma^{\prime}(z) =(−ay+1−a1−y)⋅σ′(z)
= ( − y a + 1 − y 1 − a ) ⋅ ( 1 − a ) ⋅ a ~~~~~=(-\frac{y}{a}+\frac{1-y}{1-a})\cdot(1-a)\cdot a =(−ay+1−a1−y)⋅(1−a)⋅a
= a − y ~~~~~=a-y =a−y
d W = d L d a ⋅ d a d z ⋅ d z d W 公 式 ( 3 ) dW = \frac{dL}{da}\cdot\frac{da}{dz}\cdot\frac{dz}{dW}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~公式(3) dW=dadL⋅dzda⋅dWdz 公式(3)
= d z ⋅ d z d W ~~~~~~=dz\cdot\frac{dz}{dW} =dz⋅dWdz
= d z ⋅ x ~~~~~~=dz\cdot x =dz⋅x
d b = d L d a ⋅ d a d z ⋅ d z d b 公 式 ( 4 ) db = \frac{dL}{da}\cdot\frac{da}{dz}\cdot\frac{dz}{db}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~公式(4) db=dadL⋅dzda⋅dbdz 公式(4)
= d z ⋅ d z d b ~~~~~=dz\cdot\frac{dz}{db} =dz⋅dbdz
= d z ~~~~~=dz =dz
这样我们就可以不断更新权重参数 w w w和偏置项 b b b,使得损失函数 L ( a , y ) L(a,y) L(a,y)越来越小。
2、含有一个隐层的神经网络
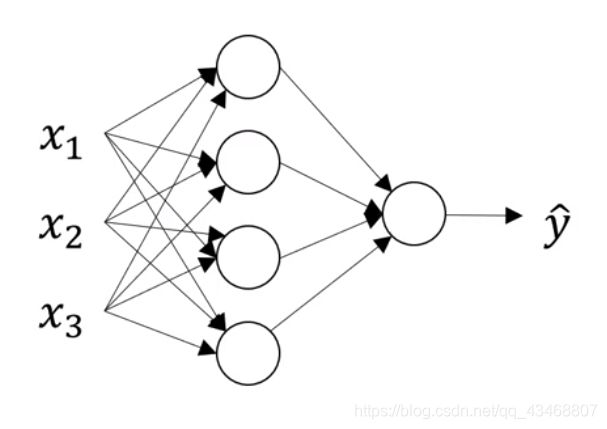
上图中有三个输入 x 1 、 x 2 、 x 3 x_1、x_2、x_3 x1、x2、x3,一个隐层,该隐层中有四个结点,一个输出层。
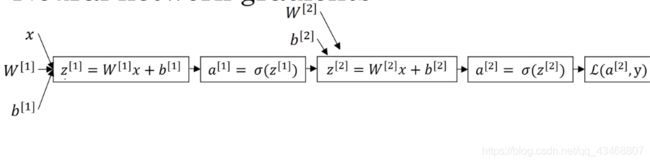
上图是神经网络正向传播过程,下图就是BP算法实现过程

d a [ 2 ] = d L d a [ 2 ] ⋅ L ( a , y ) 公 式 ( 1 ) da^{[2]}=\frac{dL}{da^{[2]}}\cdot L(a,y)~~~~~~~~~~~~~~~~~~~~~~~~~~~公式(1) da[2]=da[2]dL⋅L(a,y) 公式(1)
= − y a [ 2 ] + 1 − y 1 − a [ 2 ] ~~~~~~~~~=-\frac{y}{a^{[2]}}+\frac{1-y}{1-a^{[2]}} =−a[2]y+1−a[2]1−y
d z [ 2 ] = d L d a [ 2 ] ⋅ d a [ 2 ] d z [ 2 ] 公 式 ( 2 ) dz^{[2]} = \frac{dL}{da^{[2]}}\cdot \frac{da^{[2]}}{dz^{[2]}}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~公式(2) dz[2]=da[2]dL⋅dz[2]da[2] 公式(2)
= a [ 2 ] − y ~~~~~~~~~=a^{[2]}-y =a[2]−y
d W [ 2 ] = d L d a [ 2 ] ⋅ d a [ 2 ] d z [ 2 ] ⋅ d z [ 2 ] d W [ 2 ] 公 式 ( 3 ) dW^{[2]} = \frac{dL}{da^{[2]}}\cdot\frac{da^{[2]}}{dz^{[2]}}\cdot\frac{dz^{[2]}}{dW^{[2]}}~~~~~~~~~~~~~~~~~~~公式(3) dW[2]=da[2]dL⋅dz[2]da[2]⋅dW[2]dz[2] 公式(3)
= d z [ 2 ] ⋅ a [ 1 ] T ~~~~~~~~~~=dz^{[2]}\cdot a^{[1]T} =dz[2]⋅a[1]T
将 公 式 ( 2 ) 代 入 公 式 ( 3 ) 中 可 算 出 最 终 结 果 , 此 处 和 下 面 就 不 再 计 算 了 将公式(2)代入公式(3)中可算出最终结果,此处和下面就不再计算了 将公式(2)代入公式(3)中可算出最终结果,此处和下面就不再计算了
d b [ 2 ] = d L d a [ 2 ] ⋅ d a [ 2 ] d z [ 2 ] ⋅ d z [ 2 ] d b [ 2 ] 公 式 ( 4 ) db^{[2]} = \frac{dL}{da^{[2]}}\cdot\frac{da^{[2]}}{dz^{[2]}}\cdot\frac{dz^{[2]}}{db^{[2]}}~~~~~~~~~~~~~~~~~~~~~~~公式(4) db[2]=da[2]dL⋅dz[2]da[2]⋅db[2]dz[2] 公式(4)
= d z [ 2 ] ~~~~~~~~=dz^{[2]}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ =dz[2] 将公式(2)带入公式(4)中$
d a [ 1 ] = d L d a [ 2 ] ⋅ d a [ 2 ] d z [ 2 ] ⋅ d z [ 2 ] d a [ 1 ] 公 式 ( 5 ) da^{[1]}=\frac{dL}{da^{[2]}}\cdot\frac{da^{[2]}}{dz^{[2]}}\cdot\frac{dz^{[2]}}{da^{[1]}}~~~~~~~~~~~~~~~~~~~~~~~公式(5) da[1]=da[2]dL⋅dz[2]da[2]⋅da[1]dz[2] 公式(5)
= d z [ 2 ] ⋅ d z [ 2 ] d a [ 1 ] ~~~~~~~~~=dz^{[2]}\cdot \frac{dz^{[2]}}{da^{[1]}} =dz[2]⋅da[1]dz[2]
= W [ 2 ] T ⋅ d z [ 2 ] ~~~~~~~~~=W^{[2]T}\cdot dz^{[2]}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ =W[2]T⋅dz[2] 将公式(2)带入公式(5)中$
d z [ 1 ] = d L d a [ 2 ] ⋅ d a [ 2 ] d z [ 2 ] ⋅ d z [ 2 ] d a [ 1 ] ⋅ d a [ 1 ] d z [ 1 ] 公 式 ( 6 ) dz^{[1]}=\frac{dL}{da^{[2]}}\cdot\frac{da^{[2]}}{dz^{[2]}}\cdot\frac{dz^{[2]}}{da^{[1]}}\cdot\frac{da^{[1]}}{dz^{[1]}}~~~~~~~~~~~~~~公式(6) dz[1]=da[2]dL⋅dz[2]da[2]⋅da[1]dz[2]⋅dz[1]da[1] 公式(6)
= d a [ 1 ] ⋅ d a [ 1 ] d z [ 1 ] ~~~~~~~~~=da^{[1]}\cdot \frac{da^{[1]}}{dz^{[1]}} =da[1]⋅dz[1]da[1]
= W [ 2 ] T ⋅ d z [ 2 ] ∗ a [ 1 ] ′ ~~~~~~~~~=W^{[2]T}\cdot dz^{[2]} *{a^{[1]}}^{\prime} =W[2]T⋅dz[2]∗a[1]′
= W [ 2 ] T ⋅ d z [ 2 ] ∗ σ ′ ( z [ 1 ] ) ~~~~~~~~~=W^{[2]T}\cdot dz^{[2]}*\sigma^{\prime}(z^{[1]})~~~~~~~~~~~~~~ =W[2]T⋅dz[2]∗σ′(z[1]) 将公式(2)带入公式(6)中$
公式中各个参数矩阵的维度如下:
W [ 2 ] ( 1 , 4 ) W [ 1 ] ( 4 , 3 ) W^{[2]}~(1,4)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~W^{[1]}~(4,3) W[2] (1,4) W[1] (4,3)
b [ 2 ] ( 1 , 1 ) b [ 1 ] ( 4 , 1 ) b^{[2]}~(1,1)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~b^{[1]}~(4,1) b[2] (1,1) b[1] (4,1)
a [ 2 ] ( 1 , 1 ) a [ 1 ] ( 4 , 1 ) a^{[2]}~(1,1)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~a^{[1]}~(4,1) a[2] (1,1) a[1] (4,1)
z [ 2 ] , d z [ 2 ] ( 1 , 1 ) z [ 1 ] , d z [ 1 ] ( 4 , 1 ) z^{[2]}~,dz^{[2]}~~(1,1)~~~~~~~~~~~~~~~~~~~~z^{[1]}~,dz^{[1]}~(4,1) z[2] ,dz[2] (1,1) z[1] ,dz[1] (4,1)
公式说明
1、公式(3)的结果为 d W [ 2 ] = d z [ 2 ] ⋅ a [ 1 ] T dW^{[2]}=dz^{[2]}\cdot a^{[1]T} dW[2]=dz[2]⋅a[1]T,其中对 a [ 1 ] a^{[1]} a[1]求转置的原因如下:
对 W [ 2 ] 求 偏 导 : d W [ 2 ] = d L d a [ 2 ] ⋅ d a [ 2 ] d z [ 2 ] ⋅ d z [ 2 ] d W [ 2 ] 对W^{[2]}求偏导:dW^{[2]} = \frac{dL}{da^{[2]}}\cdot\frac{da^{[2]}}{dz^{[2]}}\cdot\frac{dz^{[2]}}{dW^{[2]}} 对W[2]求偏导:dW[2]=da[2]dL⋅dz[2]da[2]⋅dW[2]dz[2]
化 简 可 得 : d W [ 2 ] = d z [ 2 ] ⋅ d z [ 2 ] d W [ 2 ] 化简可得: dW^{[2]}=dz^{[2]}\cdot \frac{dz^{[2]}}{dW^{[2]}} 化简可得:dW[2]=dz[2]⋅dW[2]dz[2]
其 中 d z [ 2 ] 在 公 式 ( 2 ) 已 经 求 出 , 因 此 只 需 求 出 d z [ 2 ] d W [ 2 ] 其中 ~dz^{[2]}~在公式(2)已经求出,因此只需求出\frac{dz^{[2]}}{dW^{[2]}} 其中 dz[2] 在公式(2)已经求出,因此只需求出dW[2]dz[2]
因 为 z [ 2 ] = W [ 2 ] x + b [ 2 ] 因为~~z^{[2]}=W^{[2]}x+b^{[2]} 因为 z[2]=W[2]x+b[2]
= W [ 2 ] a [ 1 ] + b [ 2 ] ~~~~~~~~~~~~~~~~=W^{[2]}a^{[1]}+b^{[2]} =W[2]a[1]+b[2]
用 矩 阵 表 示 为 用矩阵表示为 用矩阵表示为 z [ 2 ] ( 1 , 1 ) = W [ 2 ] ( 1 , 4 ) a [ 1 ] ( 4 , 1 ) + b [ 2 ] ( 1 , 1 ) z^{[2]}(1,1)=W^{[2]}(1,4)~~a^{[1]}(4,1)+b^{[2]}(1,1) z[2](1,1)=W[2](1,4) a[1](4,1)+b[2](1,1)
( 1 ) 、 d z [ 2 ] 中 如 果 不 给 a [ 1 ] 加 转 置 结 果 为 (1)、dz^{[2]}中如果不给~a^{[1]}加转置结果为 (1)、dz[2]中如果不给 a[1]加转置结果为
d W [ 2 ] ( 1 , 4 ) = d z [ 2 ] ( 1 , 1 ) ⋅ a [ 1 ] ( 4 , 1 ) ~dW^{[2]}(1,4)=dz^{[2]}(1,1)~\cdot ~a^{[1]}(4,1) dW[2](1,4)=dz[2](1,1) ⋅ a[1](4,1)
而 ( 1 , 1 ) ⋅ ( 4 , 1 ) = ( 1 , 1 ) ≠ ( 1 , 4 ) ~~~~~~~~~~~~~~~~~而~~~~~(1,1) \cdot(4,1)=(1,1) \neq(1,4) 而 (1,1)⋅(4,1)=(1,1)=(1,4)
( 2 ) 、 当 d z [ 2 ] 中 给 a [ 1 ] 加 转 置 时 结 果 为 (2)、当dz^{[2]}中给~a^{[1]}加转置时结果为 (2)、当dz[2]中给 a[1]加转置时结果为
d W [ 2 ] ( 1 , 4 ) = d z [ 2 ] ( 1 , 1 ) ⋅ a [ 1 ] T ( 1 , 4 ) ~dW^{[2]}(1,4)=dz^{[2]}(1,1)~\cdot ~a^{[1]T}(1,4) dW[2](1,4)=dz[2](1,1) ⋅ a[1]T(1,4)
而 ( 1 , 1 ) ⋅ ( 1 , 4 ) = ( 1 , 1 ) = ( 1 , 4 ) 此 时 等 式 成 立 ~~~~~~~~~~~~~~~~~而~~~~~(1,1) \cdot(1,4)=(1,1) =(1,4)~~此时等式成立 而 (1,1)⋅(1,4)=(1,1)=(1,4) 此时等式成立
公式(5)和公式(6)中加入 W [ 2 ] T W^{[2]}T W[2]T的原因与上述相同。因此,在计算过程中必须保证矩阵的维度互相匹配。
2、公式(6)的结果中使用 * 乘积,而不是矩阵乘积原因如下:
d z [ 1 ] = W [ 2 ] T ⋅ d z [ 2 ] ∗ σ ′ ( z [ 1 ] ) dz^{[1]}=W^{[2]T}\cdot dz^{[2]}*\sigma^{\prime}(z^{[1]}) dz[1]=W[2]T⋅dz[2]∗σ′(z[1])
使 用 矩 阵 维 度 表 示 为 使用矩阵维度表示为 使用矩阵维度表示为
( 4 , 1 ) = ( 4 , 1 ) ⋅ ( 1 , 1 ) ∗ ( 4 , 1 ) (4,1) = (4,1)\cdot(1,1)*(4,1) (4,1)=(4,1)⋅(1,1)∗(4,1) ( 4 , 1 ) = ( 4 , 1 ) ∗ ( 4 , 1 ) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(4,1) = (4,1)*(4,1) (4,1)=(4,1)∗(4,1)
此时两个矩阵的维度都为 ( 4 , 1 ) (4,1) (4,1),此处的乘积为哈达马积(*),其元素定义为两个矩阵对应元素的乘积 的m×n矩阵。
以上就是我对反向传播(BP)算法的总结。