4、多个特征变量的线性回归

4、多个特征变量的线性回归

4.1多功能

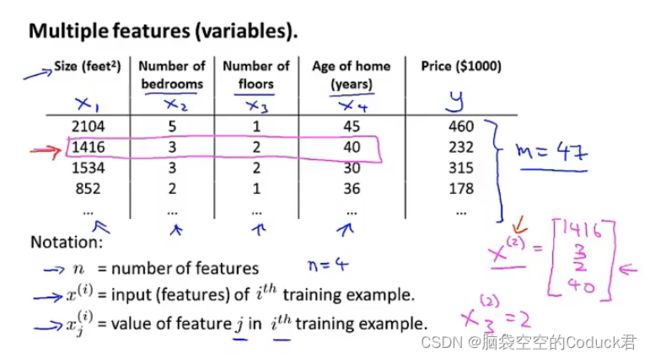
n是样本特征数量
$x^{(i)}$是第i个训练样本的特征值（包括每个特征），相当于一个向量
$x_j^{(i)}$是第i个训练样本中的第j个特征量的值

多元线性回归：
$$h\theta (x)={\theta }_0\ast x_0+{\theta }_1\ast x_1+{\theta }_2\ast x_2+\dots +{\theta }_n\ast x_n(x_0=1)$$
θ = [ θ 0 θ 1 θ 2 … θ n ] (2) \theta= \begin{bmatrix} \theta_0 \\ \theta_1\\ \theta_2\\ …\\ \theta_n \end{bmatrix} \tag{2} θ= ​θ0​θ1​θ2​…θn​​ ​(2)
x = [ x 0 x 1 x 2 … x n ] (2) x= \begin{bmatrix} x_0 \\ x_1\\ x_2\\ …\\ x_n \end{bmatrix} \tag{2} x= ​x0​x1​x2​…xn​​ ​(2)
$$h\theta (x)={\theta }^T\ast x$$

4.2多元梯度下降法

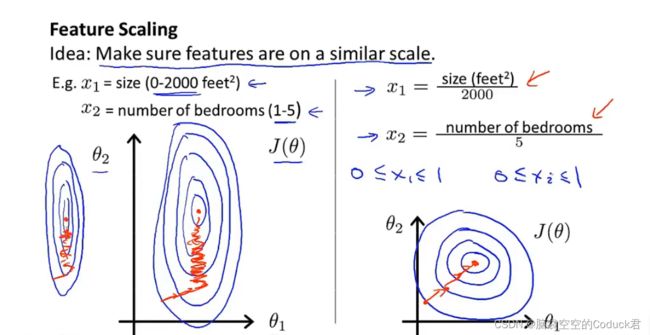
4.3特征缩放

数量级的差异将导致量级较大的属性占据主导地位
数量级的差异将导致迭代收敛速度减慢
我们需要把数据处理在相近似的取值范围内

均值归一化：
$$x_i=\frac{x_i-u_i}{s_i}$$
$u_i$：该特征所有样本的平均值
$s_i$:标准差，即最大值-最小值
处理后的数据均值为0，标准差为1

4.4如何取学习率

纵轴是$J(\theta )$的取值，横轴是迭代次数，该图可以帮助我们判断梯度下降算法是否收敛，是否正常工作

自动收敛测试：通过设定一个特定的阀值，当在某次迭代中$J(\theta )$减小小于阀值，则声明收敛

---

非正常收敛

---

$\alpha$过小，收敛过慢，$\alpha$过大，可能不收敛

尝试一系列$\alpha$值，绘制$J(\theta )$随迭代次数变化曲线，选择使$J(\theta )$快速下降的一个$\theta$值，将其作为我们较为合适的学习率

4.5特征选择和多项式模型

特征选择目的：
● 减少训练数据大小，加快模型训练速度。

● 减少模型复杂度，避免过拟合。

● 特征数少，有利于解释模型。

● 如果选择对的特征子集，模型准确率可能会提升。

在上图例子中，通过定义Area(frontage$\times$depth)新的特征，简化了模型

---

利用其它多项式模型来更好地拟合数据

对次方的处理实际上是先对特征变量进行处理

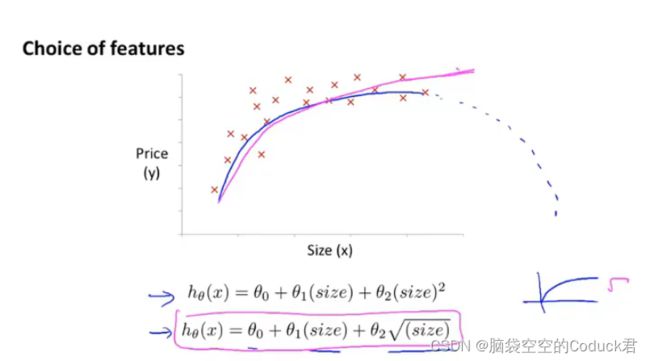
目的：为了更好地拟合我们的样本数据变化图像，我们可根据我们所了解的多项式函数的变化图像，来构建多项式模型来构建更好、更加拟合数据的模型
例如上图，为了保证模型后半段不像二次多项式模型后半段呈下降趋势，我们可以选择三次多项式模型或是平方根多项式模型

4.6正规方程（区别于迭代法的直接解法）

正规方程相当于找到模型的极小值点（求导为0）

但一个个遍历每个$\theta$参数的偏导显然是麻烦的，所以我们选择下面的公式进行计算

X被称为设计矩阵
正规方程：
$$\theta =(X\ast X^T{)}^{-1}\ast X^T\ast y$$
$\theta$即为我们需要的参数矩阵

---

如何选择梯度下降法和正规方程
1、梯度下降法
缺点：需要选择学习速率$\alpha$，额外工作；需要迭代，计算速度较慢
优点：对于多特征变量（n大）仍能很好地运作
2、正规方程
缺点：对于多特征变量（n大）计算会很慢
优点：不用选择$\alpha$;不需要迭代

通常情况，n大于10000考虑梯度下降，小于10000考虑正规方程

---

正规方程矩阵不可逆情况：

两种情况：
1、有多余的特征变量——>删除多余特征变量
2、特征变量过多——>在影响不大的情况下，删除一些特征变量或考虑使用正规化方法