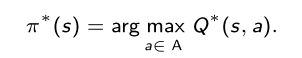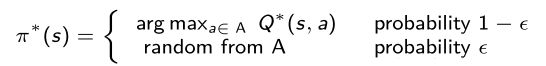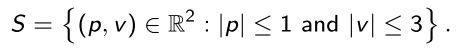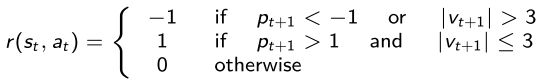Reinforcement Learning (RL) is a increasing subset of Machine Learning and one of the most important frontiers of Artificial Intelligence, since it has gained great popularity in the last years with a lot of successful real-world applications in robotics, games and many other fields. It denotes a set of algorithms that handle sequential decision-making and have the ability to take intelligent decisions depending on their local environment.
强化学习(RL)是机器学习的一个越来越多的子集,也是人工智能最重要的前沿领域之一,因为近年来它在机器人,游戏和许多其他领域的许多成功的实际应用中获得了广泛的欢迎。 它表示一组处理顺序决策并能够根据其本地环境做出智能决策的算法。
A RL algorithm can be described as a model that indicates to an agent which set of actions it should take within a closed environment in order to to maximize a predefined overall reward. Generally speaking, the agent tries different sets of actions, evaluating the total obtained return. After many trials, the algorithm learns which actions give a greater reward and establishes a pattern of behavior. Thanks to this, it is able to tell the agent which actions to take in every condition.
RL算法可以描述为一个模型,该模型向代理指示其应在封闭环境中采取哪些动作集以最大化预定义的总体奖励。 一般来说,代理尝试不同的操作集,评估获得的总回报。 经过多次试验,该算法了解到哪些操作可带来更大的回报,并建立行为模式。 因此,它可以告诉代理在每种情况下应采取的操作。
The goal of RL is to capture more complex structures and use more adaptable algorithms than classical Machine Learning, infact RL algorithms are more dynamic in their behavior compared to classical Machine Learning ones.
RL的目标是捕获比传统机器学习更复杂的结构并使用更多适应性算法,与传统机器学习相比,实际RL算法的行为更具动态性。
应用领域 (Applications)
Let’s see some examples of applications based on RL:
让我们看一些基于RL的应用程序示例:
Robotics - RL can be used for high-dimensional control problems and for various industrial applications.
机器人技术 -RL可用于高维控制问题以及各种工业应用。
Text mining - RL, along with a text generation model, can be used to develop a system that is able to produce highly readable summaries of long texts.
文本挖掘 -RL与文本生成模型一起可以用于开发能够生成高度可读的长文本摘要的系统。
Trade execution - Major companies in the financial industry use RL algorithms to improve their trading strategy.
交易执行 -金融行业的主要公司使用RL算法来改善其交易策略。
Healthcare - RL is useful for medication dosing, and for the optimization of treatment for people suffering from chronic clinical trials, etc.
医疗保健 -RL对于药物剂量以及对患有慢性临床试验的人的治疗优化等有用。
Games -RL is famous for being the main algorithm used to solve different games and to achieve superhuman performances.
游戏 -RL以解决各种游戏和实现超人表演的主要算法而闻名。
演员们 (Actors)
RL algorithms are based on Markov Decision Process (MDP). A Markov Decision Processes is a special stochastic time control process for decision making. The main actors of a RL algorithm are:
RL算法基于马尔可夫决策过程(MDP)。 马尔可夫决策过程是用于决策的特殊随机时间控制过程。 RL算法的主要参与者是:
Agent: an entity which performs actions in an environment in order to optimize a long-term reward;
代理商 :在环境中执行操作以优化长期奖励的实体;
Environment: the scenario in which the agent takes decisions;
环境 :代理做出决定的场景;
Set of states (S): the set of all the possible states s of the environment, where the state describes the current situation of the environment;
状态集 ( S ):环境的所有可能状态s的集合,其中状态描述了环境的当前状况;
Set of actions (A): the set of all the possible actions a that can be performed by the agent;
动作组 ( A ):代理可以执行的所有可能动作a的组;
State transition model P (s_0|s , a): describes the probability that the environment state changes in s_0 when the agent performs the action a at state s, for every states s, s_0 and action a;
状态转换模型P(s_0 | s,a) :描述了代理针对状态s , s_0和动作a在状态s执行动作a时,环境状态在s_0中变化的概率;
Reward (r = R(s , a)): a function that indicates the immediate the real valued reward for taking action a at state s;
奖励(r = R(s,a)) :指示立即在状态s采取行动a的实际价值奖励的函数;
Episode (rollout): it’s a sequence of states st and actions at for t that varies from 0 to a final value L (that is called horizon and can eventually be infinite); the agent starts in a given state of its environment; at each timestep t the agent observes the current state s_t ∈ S and consequently takes an action a_t ∈ A; the state evolves into a new state s_(t+1), that depends only on the state s_t and on the action a_t , according to the state transition model; the agent obtains a reward r_t; then the agent observes the new state s_(t+1)∈ S and the loop restarts;
情节(推出) :它是状态为st的动作序列,在t处处于从0到最终值L (称为地平线,最终可能是无限大)的状态; 代理在其环境的给定状态下启动; 代理在每个时间步长t观察当前状态s_t∈S并因此采取行动a_t∈A ; 根据状态转换模型,状态演变为仅取决于状态s_t和动作a_t的新状态s_(t + 1) ; 代理商获得奖励r_t ; 然后,代理观察到新状态s_(t + 1)∈S ,然后循环重新开始;
Policy function: a policy can be deterministic (π (s)) or stochastic ((a|s)): a deterministic policy π (s) indicates the action a performed by the the agent when the environment is in the state s (a = π (s)); a stochastic policy π (a|s) is a function that describe the probability that action a is performed by the the agent when the environment is in the state s. Once that the policy is specified, the new state only depends on the policy and on the state transaction model;
策略功能 :策略可以是确定性( π(s) )或随机( (a | s) ):确定性策略π(s)表示环境处于状态s( a时,代理执行的动作a =π(s) ); 随机策略π(a | s)是描述环境处于状态s时由代理执行动作a的概率的函数。 一旦指定了策略,新状态就仅取决于策略和状态事务模型;
Return G_t : the total long term reward with discount obtained at the end of the episode, according to the immediate reward of the current timestep and of every following timesteps, and to the the discount factor γ < 1:
返回G_t :根据当前时间步长和随后每个时间步长的即时奖励以及折扣因子γ<1,在情节结束时获得的总长期奖励和折扣
Value function V(s): the expected long-term return at the end of the episode, starting from state s at current timestep t:
值函数V(s) :情节结束时的预期长期回报,从当前时间步长t的状态s开始:
Q-Value or Action-Value function Q(s , a): the expected long-term return at the end of the episode, starting from state s at current timestep, and performing action a;
Q值或动作值函数Q(s,a) :情节结束时的预期长期回报,从当前时间步的状态s开始,并执行动作a ;
The Bellman equation: the theoretical core in most RL algorithms; according to it, the current value function is equal to the current reward plus itself evaluated at the next step and discounted by γ (we recall that in the equation P is the model transition model):
Bellman方程 :大多数RL算法的理论核心; 根据它,当前值函数等于当前奖励加上在下一步中评估的自身,并减去γ(我们回想起来,方程P中是模型转换模型):
最优政策 (Optimal policy)
The maximum of the action value function, as the policy changes, is referred as the optimal action value function Q*(s , a), and according to Bellman equation is given by
当策略改变时,动作值函数的最大值称为最佳动作值函数Q *(s,a) ,根据Bellman方程,公式为
Then the optimal policy π*(s) is given by the action that maximizes the action value function:
然后,由使动作值函数最大化的动作给出最佳策略π*(s) :
The problem is that in most real cases the state transition model and the reward function are unknown, so it’s necessary to learn them from sampling in order to estimate the optimal action value function and the best policy. For these reasons RL algorithms are used, in order to take the actions in the environment, observe and learn the dynamics of the model, estimate the optimal value function and the optimal policy, and improve the rewards.
问题在于,在大多数实际情况下,状态转换模型和奖励函数都是未知的,因此有必要从采样中学习它们,以估算最佳作用值函数和最佳策略。 由于这些原因,为了在环境中采取行动,观察和学习模型的动力学,估计最优价值函数和最优策略以及提高回报,使用了RL算法。
勘探开发困境 (Exploration-exploitation dilemma)
Exploration is the training on new data points, while exploitation is the use of the previously captured data. If we keep searching for the best action in every iteration we might remain stopped in a limited set of states without being able to explore the entire environment. To get out of this suboptimal set, generally it’s used a strategy called ϵ-greedy: when we select the best action, there is small a probability ϵ that a random action is chosen.
探索是对新数据点的培训,而探索是对先前捕获的数据的使用。 如果我们在每次迭代中一直在寻找最佳操作,那么我们可能会停留在有限的一组状态中而无法浏览整个环境。 为了摆脱这个次优集合,通常使用一种称为ϵ贪婪的策略:当我们选择最佳动作时,选择随机动作的可能性很小。
方法 (Approaches)
There are 3 main possible approaches that we can use when we implement a RL algorithm:
实现RL算法时,可以使用3种主要方法:
Value-based methods - A Value-based algorithm approximates the optimal value function, or the optimal action value function, by continuously improving their estimate. Usually the value function or the action value function are initialized randomly, then they are continuously updated until they converge. A Value-based algorithm is guaranteed to converge to the optimal values.
基于价值的方法-基于价值的算法通过不断改进估算值来逼近最佳价值函数或最佳行动价值函数。 通常,值函数或操作值函数是随机初始化的,然后不断进行更新,直到收敛为止。 基于值的算法可保证收敛到最佳值。
Policy-based methods - A Policy-based algorithm looks for a policy such that the action performed at each state is optimal to gain maximum reward in the future. It redefines the policy at each step and computes the value function according to this new policy until the policy converges. A Policy-based method is also guaranteed to converge to the optimal policy, and often takes less iterations to converge than the value-based algorithms.
基于策略的方法-基于策略的算法会寻找一种策略,以便在每个状态下执行的操作都是最佳的,以便将来获得最大的回报。 它在每个步骤重新定义策略,并根据此新策略计算值函数,直到策略收敛为止。 还可以确保基于策略的方法收敛于最佳策略,并且与基于值的算法相比,收敛所需的迭代次数更少。
Model-based methods - A Model-based algorithm learns a virtual model starting from the original environment, and the agent learns how to perform in the virtual model. It uses a reduced number of interactions with the real environment during the learning phase, then it builds a new model based on these interactions, uses this model to simulate the further episodes, and and get the results returned by the virtual model.
基于模型的方法-基于模型的算法从原始环境开始学习虚拟模型,而代理则学习如何在虚拟模型中执行。 它在学习阶段使用较少的与实际环境的交互,然后基于这些交互建立一个新的模型,使用该模型来模拟进一步的情节,并获得虚拟模型返回的结果。
基于价值的方法 (Value-based methods)
值函数近似 (Value Function Approximation)
The Value Function Approximation is one of the most classical Value-based methods. Its goal is to estimate the optimal policy π*(s) by iteratively approximating the optimal action value function Q*(s , a). We start considering a parametric action value function Q^(s , a , w), where w is a vector of parameters. We initialize randomly the vector w and we iterate on every step of every episode. For every iteration, given the state s and the action a, we observe the reward R(s , a) and the new state s’. According to the obtained reward we update the parameters using the gradient descent:
值函数逼近是最经典的基于值的方法之一。 其目标是通过迭代逼近最佳作用值函数Q *(s,a)来估算最佳策略π*(s ) 。 我们开始考虑参数作用值函数Q ^(s,a,w) ,其中w是参数的向量。 我们随机初始化向量w,并在每个情节的每个步骤上进行迭代。 对于每次迭代,给定状态s和动作a ,我们观察到奖励R(s,a)和新状态s' 。 根据获得的奖励,我们使用梯度下降更新参数:
In the equation, α is the learning rate. It can be shown that this process converges, and the obtained action value function is our approximation of the optimal action value function. In most of the real cases the better choice for the parametric action value function Q^(s , a , w) is a Neural Network, and then the vector of parameters w is given by the vector of the weights of the Neural Network.
在等式中,α是学习率。 可以证明,该过程收敛,并且获得的作用值函数是最优作用值函数的近似值。 在大多数实际情况下,参数作用值函数Q ^(s,a,w)的更好选择是神经网络,然后参数w的向量由神经网络权重的向量给出。
Value Function Approximation algorithm:
值函数近似算法:
深度Q网络 (Deep Q-Networks)
A Deep Q-Network is a combination of Deep Learning and RL, since it is a Value Function Approximation algorithm where the parametric action value function Q^(s , a , w) is a Deep Neural Network, and in particular a Convolutional Neural Network. Moreover, a Deep Q-Network overcomes unstable learning using mainly 2 techniques
深度Q网络是深度学习和RL的组合,因为它是一种值函数逼近算法,其中参数作用值函数Q ^(s,a,w)是深度神经网络,尤其是卷积神经网络。 此外,深度Q网络主要使用两种技术来克服学习不稳定的问题
Target Network - The model updates could be very unstable since the real target changes each time the model updates itself. The solution is to create a Target Network Q^(s’,a’,w’), which is a copy of the training model that is updated less frequently, for example every thousands steps (we indicate as w’ the weights of the Target Network). In every model update with the gradient descent, the Target Network is used as target in place of the model itself:
目标网络-模型更新可能非常不稳定,因为实际目标每次模型更新时都会更改。 解决方案是创建一个目标网络Q ^(s',a',w') ,它是训练模型的副本,其更新频率较低,例如每千步更新一次(我们将w的权重表示为w'目标网络)。 在每次使用梯度下降的模型更新中,目标网络都将用作模型本身的目标:
Experience Replay - In the described algorithm several consecutive updates are performed using data from the same episode, and this can cause overfitting. To solve this, it is created an Experience Replay buffer that stores the four-tuples (s,a,r,s’) of all the different episodes, and randomly select a batch of tuples each time the model is updated. This solution has 3 advantages: reduces overfitting, increases learning speed with mini-batches, and reuses past tuples to avoid forgetting.
体验重播-在描述的算法中,使用来自同一情节的数据执行多次连续更新,这可能会导致过拟合。 为了解决这个问题,它创建了一个“体验重播”缓冲区,该缓冲区存储所有不同情节的四元组( s , a , r , s' ),并在每次更新模型时随机选择一批元组。 该解决方案具有3个优点:减少过度拟合,使用迷你批处理提高学习速度,并重用过去的元组以避免遗忘。
拟合Q迭代 (Fitted Q-Iteration)
Another popular Value-based algorithm is Fitted Q-Iteration. Consider the deterministic case, in which we have that the new state s’ is uniquely determined by the state s and the action a according to some a function f , then we can write s’ = f (s , a). Let L be the horizon, possibly infinite, and we recall that the horizon is the length of all the episodes. The goal of this algorithm is to estimate the optimal action value function. By the Bellman equation, the optimal action value function Q*(s , a) can be seen as the application of an operator H to the action value function Q(s , a):
另一个流行的基于值的算法是拟合Q迭代。 考虑确定性情况,在这种情况下,新状态s'由状态s和动作a根据某个函数f唯一地确定,那么我们可以写出s'= f(s,a) 。 令L为地平线,可能是无限的,并且我们记得地平线是所有情节的长度。 该算法的目标是估计最佳作用值函数。 通过Bellman方程,最佳作用值函数Q *(s,a)可以看作是算子H在作用值函数Q(s,a)上的应用 :
Consider now a temporal horizon N less than or equal to the horizon L, and denote by Q_N (s , a) the action value function over N steps defined by the application of the just defined operator H to the action value function Q_(N−1) (s , a), with
现在考虑小于或等于水平线L的时间水平线N ,并用Q_N(s,a)表示N步上的动作值函数,该步长由刚刚定义的算子H应用于动作值函数Q_(N− 1)(s,a)
It is possible to show that this sequence of N-step action value functions Q_N (s , a) converges to the optimal action value function Q*(s , a) as N → L. Thanks to this, it’s possible to build an algorithm to approximate the optimal action value function Q*(s , a) iterating on N.
可以证明,这一系列的N 步动作值函数Q_N(s,a)收敛为最优动作值函数Q *(s,a)为N→L 。 因此,有可能构建一种算法来近似迭代对N的最佳作用值函数Q *(s,a) 。
Fitted Q-Iteration algorithm:
拟合Q迭代算法:
A full implementation of Fitted Q-Iteration can be found on GitHub(https://github.com/teopir/ifqi).
可以在GitHub( https://github.com/teopir/ifqi )上找到Fitted Q-Iteration的完整实现。
拟合Q迭代应用程序的示例:山上的汽车 (Example of Fitted Q-Iteration application: Car on a Hill)
Consider a car, modeled by a point mass, that is traveling on a hill with this form:
考虑以点质量为模型的汽车以这种形式在山上行驶:
The control problem goal is to bring the car in a minimum time to the top of the hill while preventing the position p of the car to become smaller than -1 and its speed v to go outside the interval [-3 , 3]. The top of the hill is reached at position p = 1.
控制问题的目标是使汽车在最短的时间内到达山顶,同时防止汽车的位置p小于-1且其速度v超出区间[-3,3] 。 在位置p = 1到达山顶。
State space - This problem has a (continuous) state space of dimension two (the position p and the speed v of the car), and we want that the absolute value of the position is less than or equal to 1, and that the absolute value of the speed is less than or equal to 3:
状态空间-这个问题具有一个(维度为2的)(连续)状态空间(汽车的位置p和速度v ),我们希望该位置的绝对值小于或等于1 ,并且速度值小于或等于3 :
Every other combination of position and speed is considered a terminal state.
位置和速度的所有其他组合都被视为终端状态。
Action space - The action a acts directly on the acceleration of the car and canonly assume two extreme values (full acceleration (a = 4) or full deceleration (a -4)). Hence the action space is given by the set
动作空间-动作a直接作用于汽车的加速度,并且只能采用两个极限值(全加速度( a = 4)或全减速度( a -4 ))。 因此动作空间由集合给定
System dynamics - The time is discretized in timesteps of 0.1 seconds. Given the state (p, v) and the action a at timestep t, we are able to compute the state (p, v) at timestep t + 1 solving with a numeric method the two differential equations related to position and speed that describe the dynamic of the system:
系统动态-时间以0.1秒的时间步长离散化。 给定状态( p , v )和时间步t的动作a ,我们能够计算出时间步t + 1的状态( p , v ),使用数值方法求解与位置和速度有关的两个微分方程系统动态:
Of course for our purpose it’s not important to understand the meaning of these equations, it’s important to understand that given state and action at timestep t, the state at timestep t + 1 in uniquely determined.
当然,出于我们的目的,了解这些方程式的含义并不重要,重要的是要了解给定的状态和时间步t的行为,时间步t +1的状态是唯一确定的。
Reward function - The reward function r(s , a) is defined through this expression:
奖励函数-奖励函数r(s,a)通过以下表达式定义:
The reward is -1 if the position is less then -1 or if the absolute value of the speed is greater than 3 because we reached a termination state but we didn’t reach the top of the hill; the reward is 1 if the position is greater than 1 and the absolute value of the speed is less than 3 because we reached the top of the hill respecting the speed limits; otherwise the reward is 0.
如果位置小于-1或速度的绝对值大于3(因为我们到达终止状态但未到达山顶),则奖励为-1 。 如果位置大于1并且速度的绝对值小于3,则奖励为1 ,因为我们遵守速度限制到达山顶; 否则奖励为0 。
Discount factor - The decay factor γ has been chosen equal to 0.95.
折现系数-选择的衰减系数γ等于0.95。
Initial point - At the begin the car stopped at the bottom of the hill (p , v) = (0.5, 0).
初始点 -在开始把车停在山上(P,V)=(0.5,0)的底部。
Regressor - The regressor used is an Extra Tree Regressor.
回归器-使用的回归器是Extra Tree Regressor。
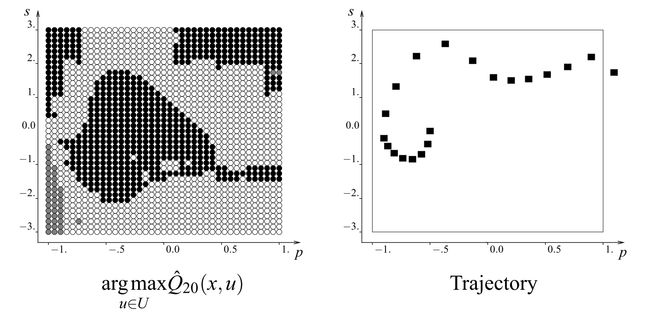
Performing the Fitted Q-Iteration for N = 1 to 50 it turns out that for N > 20 the mean squared error between action value functions Q^_N (s , a) and Q^_(N+1)(s , a) (computed on all the combinations of (p, v)) decreases quickly to 0 as N increases. For this reason the results are studied using the action state function Q^_20(s , a).
对N = 1到50进行拟合Q迭代,结果表明,对于N> 20 ,作用值函数Q ^ _N (s,a)和Q ^ _(N + 1)(s,a)之间的均方误差(根据( p , v )的所有组合计算)随N的增加Swift减小至0 。 因此,使用动作状态函数Q ^ _20(s,a)研究结果 。
In figure on the left we can see the action chosen for every combination of(position, speed), according to the action value function Q^_20(s , a) (black bullets represent deceleration, white bullets represent acceleration, gray bullets mean that the action values of deceleration and acceleration are equal).
在左图中,我们可以看到根据动作值函数Q ^ _20(s,a)为(位置,速度)的每个组合选择的动作(黑色子弹表示减速,白色子弹表示加速度,灰色子弹表示减速和加速的作用值相等)。
The optimal trajectory according to the action value function Q^_20(s , a) is represented in the figure on the right.
在右边的图中示出了根据作用值函数Q ^ _20(s,a)的最优轨迹。
政策评估方法 (Policy-valued Methods)
政策梯度 (Policy Gradient)
Policy Gradient os the most classical Policy-based method. The goal of the Policy Gradient method is to find the vector of parameters θ that maximizes the value function V (s , θ) under a parametric policy π (a|s , θ).
策略梯度是最经典的基于策略的方法。 策略梯度方法的目标是找到在参数策略π(a | s,θ)下使值函数V(s,θ)最大化的参数θ的向量。
We start considering a parametric policy π (a|s , θ) differentiable with respect to the vector of parameters θ; in particular in this case we choose a stochastic policy (in this case the method is called Stochastic Policy Gradient, however the case with a deterministic policy is very similar).
我们开始考虑相对于参数θ的矢量可微化的参数策略π(a | s,θ) ; 特别是在这种情况下,我们选择了一个随机策略(在这种情况下,该方法称为随机策略梯度,但是具有确定性策略的情况非常相似)。
We initialize randomly the vector w and we iterate on every episode. For each timestep t we generate a sequence of triplets (s, a, r) choosing the action according the parametric policy π (a|s , θ). For every timestep in the resulting sequence we compute the total long term reward with discount G_t in function of the obtained rewards:
我们随机初始化向量w,并在每个情节上进行迭代。 对于每个时间步长t,我们生成一个三元组序列( s , a , r ),该序列根据参数策略π(a | s,θ)选择动作。 对于结果序列中的每个时间步,我们根据获得的奖励的函数计算总长期奖励(折扣G_t) :
Then the vector of parameters θ_t is modified using a gradient update process
然后使用梯度更新过程修改参数θ_t的向量
In the equation α > 0 is the learning rate.
在等式中,α> 0是学习率。
It can be shown that this process converges, and the obtained process is our approximated optimal policy.
可以证明,该过程收敛,所获得的过程是我们近似的最优策略。
Policy Gradient algorithm:
策略梯度算法:
参数化策略示例 (Examples of parametric policies)
The most used parametric policies are Softmax Policy and Gaussian Policy.
最常用的参数策略是Softmax策略和高斯策略。
Softmax PolicyThe Softmax Policy consists of a softmax function that converts output to adistribution of probabilities, and is mostly used in the case discrete actions:
Softmax策略 Softmax策略包含一个softmax函数,该函数将输出转换为概率分布,并且主要用于离散操作:
In this case the explicit formula for the gradient update is given by
在这种情况下,梯度更新的显式公式为
where φ(s , a) is the feature vector related to the state and the action.
其中φ(s,a)是与状态和动作有关的特征向量。
Gaussian PolicyThe Gaussian Policy is used in the case of a continuous action space, and is given by the Gaussian function
高斯策略高斯策略用于连续动作空间时,由高斯函数给出
where µ(s) is given by φ(s) T θ, φ(s , a) is feature vector, and σ can be fixed or parametric. Also in this case we have the explicit formula for the gradient update:
其中µ(s)由φ(s) Tθ给出, φ(s,a)是特征向量,而σ可以是固定的或参数化的。 同样在这种情况下,我们具有用于渐变更新的显式公式:
政策梯度的优缺点 (Advantages and Disadvantages of Policy Gradient)
Advantages
优点
A Policy Gradient method is a simpler process compared with value-based
与基于价值的方法相比,“策略梯度”方法是一个更简单的过程
methods.
方法。
- It allows the action to be continuous with respect to the state. 它允许动作相对于状态是连续的。
- It usually has better convergence properties with respect to other methods. 相对于其他方法,它通常具有更好的收敛性。
- It avoids the growth in the usage of memory and in the computation time when the action and state sets are large, because the goal is to learn a set of parameters whose size is much smaller than that of the set of states and the set of actions. 当操作和状态集很大时,它避免了内存使用量和计算时间的增长,因为目标是要学习一组参数,这些参数的大小比状态和操作集的大小小得多。 。
- It can learn stochastic policies. 它可以学习随机策略。
- It allows the use ϵ-greedy method, so that the agent can have a probability ϵ of taking random actions. 它允许使用ϵ-贪婪方法,以便代理可以具有采取随机动作的概率ϵ。
Disadvantages
缺点
A Policy Gradient method typically converges to a local rather than global
策略梯度方法通常收敛于局部而不是全局
optimum.
最佳。
- It usually has high variance (that however can be reduced with some techniques). 它通常具有较高的方差(但是可以使用某些技术来减小该方差)。
策略渐变应用示例:CartPole (Example of Policy Gradient application: CartPole)
CartPole is a game where a pole is attached by an unactuated joint to a cart, which moves along a frictionless track. The pole starts upright.
CartPole是一款游戏,其中一根杆通过未操纵的接头连接到沿着无摩擦轨迹运动的推车上。 杆子开始直立。
The goal is to prevent the pole from falling over by increasing and reducing the cart’s velocity.
目的是通过增加和降低推车的速度来防止杆倒下。
State space - A single state is composed of 4 elements:
状态空间-单个状态由4个元素组成:
- cart position 购物车位置
- cart velocity 推车速度
- pole angle 极角
- pole angular velocity 极角速度
The game ends when the pole falls, which is when the pole angle is more than ±12°, or the cart position reaches the edge of the display.
当杆子落下时,即杆子角度大于±12°或推车位置到达显示屏边缘时,游戏结束。
Action space - The agent can take only 2 actions:
操作空间-代理只能采取2个操作:
- move the pole to the left 将杆向左移动
- move the pole to the right 将杆向右移动
Reward - For every step taken (including the termination step), the reward is increased by 1. This is obviously because we want to achieve the greatest possible number of steps.
奖励-每采取一个步骤(包括终止步骤),奖励就会增加1 。 显然,这是因为我们希望实现尽可能多的步骤。
The problem is solved with Gradient Policy method using Softmax Policy, with discount factor γ = 0.95 and learning rate α = 0.1. For every episode a maximum number of 1000 iterations is fixed.
使用Softmax策略的梯度策略方法解决了该问题,折扣系数γ= 0.95 ,学习率α= 0.1 。 对于每个情节,固定的最大迭代次数为1000。
After about 60 epochs (where 1 epoch is equal to 20 consecutive episodes) the agent learns a policy thanks to which we get a reward equal to 1000, that means that the pole doesn’t fall for all the 1000 steps of the episode.
在大约60个纪元之后(其中1个纪元等于20个连续情节),特工学会了一项政策,由于我们获得了等于1000的奖励,这意味着该情节的所有1000步都不会掉下来。
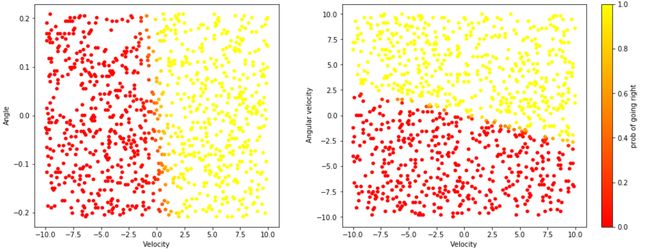
In this charts we can see how the probability to choose move left action (red points) or move right action (yellow points) vary in function of the pole angle and the cart velocity (left figure) and in function of the pole angular velocity and the cart velocity (right figure).
在此图表中,我们可以看到选择左移动作(红色点)或右移动作(黄色点)的概率如何随极角和小车速度的函数(左图)以及极角速度和推车速度(右图)。
The next chart is very interesting because we see how the average reward per epoch evolves in function of the total number of epochs, for different values of the discount γ. It’s evident that if γ is lower than 0.9, the reward doesn’t grow with the number of epochs (see the blue line), and this means that for this problem the reward of the next steps is very important to find the best policy. This is actually reasonable, given that the fundamental information to learn how to prevent the pole from falling is to know after how many steps it falls in each episode.
下一个图表非常有趣,因为对于折扣γ的不同值,我们看到每个时期的平均奖励如何随着时期总数的变化而变化。 显然,如果γ小于0.9 ,则奖励不会随着时期的增加而增加(参见蓝线),这意味着对于这个问题,下一步的奖励对于找到最佳策略非常重要。 实际上,这是合理的,因为学习如何防止极点跌落的基本信息是要知道每集跌倒了多少步。
On GitHub it’s possible to find many different implementations of this example.
在GitHub上,可以找到此示例的许多不同实现。
演员批评法 (Actor-Critic Method)
Another popular policy-based method is Actor-Critic. It is different from the Policy Gradient method because estimates both the policy and the value function, and updates both.
另一种流行的基于策略的方法是Actor-Critic。 它与“策略梯度”方法不同,因为它同时估计策略和值函数,并同时更新两者。
In Policy Gradient, the vector of parameters θ is updated using the long term reward G_t , but this estimation often has high variance. To address this issue and reduce the wide changes in the results, the idea of the Actor-Critic method is to subtract from the total reward with discount G_t a baseline b(s).
在“策略梯度”中,使用长期奖励G_t更新参数θ的向量,但此估计通常具有较高的方差。 为了解决这个问题并减少结果的广泛变化,Actor-Critic方法的想法是从折扣G_t的总奖励中减去基线b(s) 。
The obtained value δ = Gt - b(s), that is called Temporal Difference error, is used to update the vector of parameters θ in place of the long term reward G_t . The baselines can take several forms, but the most used is the estimation of the value function V(s).
所获得的值δ= Gt-b(s) (称为时间差误差)用于代替长期奖励G_t来更新参数θ的向量。 基线可以采用多种形式,但是最常用的是值函数V(s)的估计。
As in value-based methods, the value function V(s) can be learned with a Neural Network, whose output is the approximated value function V^(s , w), where w is the vector of weights. Then in every iteration the Temporal Difference error δ is used non only to adjust the vector of parameters θ, but also to update the vector of weights w.
与基于值的方法一样,可以使用神经网络学习值函数V(s) ,其输出是近似值函数V ^(s,w) ,其中w是权重的向量。 然后,在每次迭代中,均使用时间差误差δ来调整参数θ的向量,还用于更新权重向量w 。
This method is called Actor-Critic Methods, because:
该方法被称为Actor-Critic方法,因为:
The Critic estimates the value function V(s).
评论家估计值函数V(s) 。
- The Actor updates the policy distribution in the direction suggested by the Critic (as in policy gradient methods). 参与者按照评论家建议的方向更新策略分布(如策略梯度方法中一样)。
Actor-Critic algorithm:
Actor-Critic算法:
基于模型的方法 (Model-based Method)
As already underlined, a Model-based method creates a virtual model starting from the original environment, and that the agent learns how to perform in the virtual model. A Model-based method starts considering a base parametric model, and then run the following 3 steps:
如已经强调的那样,基于模型的方法从原始环境开始创建虚拟模型,并且代理学习如何在虚拟模型中执行。 基于模型的方法开始考虑基本参数模型,然后运行以下3个步骤:
Acting: the base policy π_0(a_t|s_t) is used to select the actions to perform in the real environment, in order to collect a set of observations given by the triplets (state, action, new state);
代理 :基本策略π_0(a_t | s_t)用于选择在实际环境中要执行的动作,以便收集三元组给出的一组观察值(状态,动作,新状态);
Model learning: from the collected experience, a new model m(s , a) is deduced in order to minimize the least square error between the model’s new state and the real new state; a supervised learning algorithm can be used to train a model to minimize the least square error from the sampled trajectory;
模型学习 :从收集的经验中推导出新模型m(s,a) ,以最小化模型的新状态与实际新状态之间的最小平方误差; 监督学习算法可用于训练模型,以最小化采样轨迹的最小平方误差;
Planning: the value function and the policy are updated according to the new model, in order to be used to select the actions to perform in the real environment in the next iteration.
计划 :根据新模型更新价值函数和策略,以便选择下一个迭代在实际环境中执行的操作。
One of the most used models to represent the system dynamics is the Gaussian Process, in which the prediction interpolates the observations using Gaussian distribution. Another possibility is to use the Gaussian Mixture Model, that is a probabilistic model that assumes all the data points are generated from a mixture of a finite number of Gaussian distributions with unknown parameters. It’s a sort of generalization of k-means clustering that incorporates information about the covariance structure of the data as well as the centers of the latent Gaussians.
代表系统动力学的最常用的模型之一是高斯过程,其中预测使用高斯分布对观测值进行插值。 另一种可能性是使用高斯混合模型,这是一种概率模型,它假定所有数据点都是从有限数量的高斯分布与未知参数的混合物中生成的。 这是对k均值聚类的一种概括,它包含有关数据协方差结构以及潜在高斯中心的信息。
Model based method sample algorithm:
基于模型的方法样本算法:
模型预测控制 (Model Predictive Control)
The Model Predictive Control is an evolution of the method just described. The described Model-based algorithm is vulnerable to drifting: small errors accumulate fast along the trajectory, and the search space is too big for any base policy to be covered all over. For this reasons the trajectory may arrive in areas where the model has not been learned yet. Without a proper model around these areas, it’s impossible to plan the optimal control.
模型预测控制是上述方法的改进。 所描述的基于模型的算法很容易漂移:小的错误会沿着轨迹快速累积,并且搜索空间太大,无法覆盖所有基本策略。 因此,轨迹可能到达尚未学习模型的区域。 如果没有围绕这些区域的适当模型,就不可能计划最佳控制。
To address that, instead of learning the model at the beginning, sampling and fitting of the model are performed continuously during the trajectory. Nevertheless, the previous method executes all planned actions before fitting the model again.
为了解决这个问题,代替在开始时学习模型,而是在轨迹期间连续执行模型的采样和拟合。 但是,先前的方法会在再次拟合模型之前执行所有计划的操作。
In Model Predictive Control, the whole trajectory is optimized, but only the first action is performed, then the new triplet (s, a, s’) is added to the observations and the planning is done again. This allows to take a corrective action if the current state is observed again. For a stochastic model, this is particularly helpful.
在模型预测控制中,优化了整个轨迹,但是仅执行了第一个动作,然后将新的三元组( s , a , s' )添加到观测值中,并再次进行了计划。 如果再次观察到当前状态,则可以采取纠正措施。 对于随机模型,这特别有用。
By constantly changing plan, MPC is less vulnerable to problems in the model. The new algorithm the run 5 steps, of which the first 3 are the same as the previous algorithm (acting, model learning, planning). Then we have:
通过不断更改计划,MPC不太容易受到模型问题的影响。 新算法运行5个步骤,其中前3个步骤与以前的算法相同(作用,模型学习,计划)。 然后我们有:
Acting
代理
Model learning
模型学习
Planning
规划
Execution: the first planned action is performed, and the resulting state s’ is observed;
执行 : 执行第一个计划的动作,并观察结果状态s' ;
Dataset update: the new triplet (s,a,s’) is appended to the dataset; go to step 3, every N times go to step 2 (as already seen, this means that the planning is performed every step, and that the model is fitted every N steps of the trajectory).
数据集更新 :将新的三元组( s , a , s' )附加到数据集; 转到第3步,每N次转到第2步(如前所述,这意味着每步执行一次计划,并且轨迹的每N步拟合一次模型)。
基于模型的方法的优缺点 (Model-based Methods Advantages and Disadvantages)
Model-based RL has a strong advantage of being very efficient with few samples, since many models behave linearly at least in the local proximity.
基于模型的RL具有非常有效的优势,即使用少量样本非常有效,因为许多模型至少在局部附近具有线性行为。
Once the model and the reward function are known, the planning of the optimal controls doesn’t require additional sampling. Generally the learning phase is fast, since there is no need to wait for the environment to respond nor to reset the environment to some state in order to resume learning.
一旦知道了模型和奖励函数,就可以对最佳控制进行计划,而无需额外采样。 通常,学习阶段很快,因为无需等待环境响应或将环境重置为某种状态即可恢复学习。
On the downside, if the model is inaccurate, we risk learning something completely different from the reality. Another point worth nothing is that Model-based algorithm still use Model-free methods either to construct the model or in the planning and simulation phases.
不利的一面是,如果模型不准确,我们就有可能学习与现实完全不同的东西。 另一点毫无价值的是,基于模型的算法在构建模型或在规划和仿真阶段仍然使用无模型方法。
结论 (Conclusions)
This article is a high-level structural overview of many classical RL algorithms. However it’s ovious that there are a lot of variants in each model family that we’ve not covered. For example, in the Deep Q-Networks family, double Deep Q Networks give very interesting results.
本文是许多经典RL算法的高级结构概述。 但是很明显,每个模型系列都有很多我们没有介绍的变体。 例如,在Deep Q-Networks系列中,双重Deep Q Networks给出了非常有趣的结果。
The main challenge in RL lays in preparing the simulation environment and choosing the most suitable approach. Those aspects are highly dependent on the task to be performed and are very important because many real world problems have enormous state or action spaces that must be represented efficiently and comprehensively.
RL中的主要挑战在于准备仿真环境并选择最合适的方法。 这些方面在很大程度上取决于要执行的任务,并且非常重要,因为许多现实世界中的问题都有巨大的状态或动作空间,必须有效,全面地表示出来。
The other main tasks are to optimize the rewards in order to obtain the desired results, to set up the system in oder to let the learning process converge to the optimum in a reasonable time, and to avoid overfitting and forgetting.
其他主要任务是优化奖励以获得期望的结果,合理设置系统以使学习过程在合理的时间内收敛到最佳状态,并避免过度拟合和遗忘。
翻译自: https://medium.com/@marcodelpra/introduction-to-reinforcement-learning-c99c8c0720ef