（二）机器学习的流程概述，线性规划，图像分类

前言

  本文主要讲述机器学习的大致流程，以及针对图像的线性分类器，包括线性规划、随机梯度下降、损失函数、数据处理等。通过本文讲述上一文中的这个图像：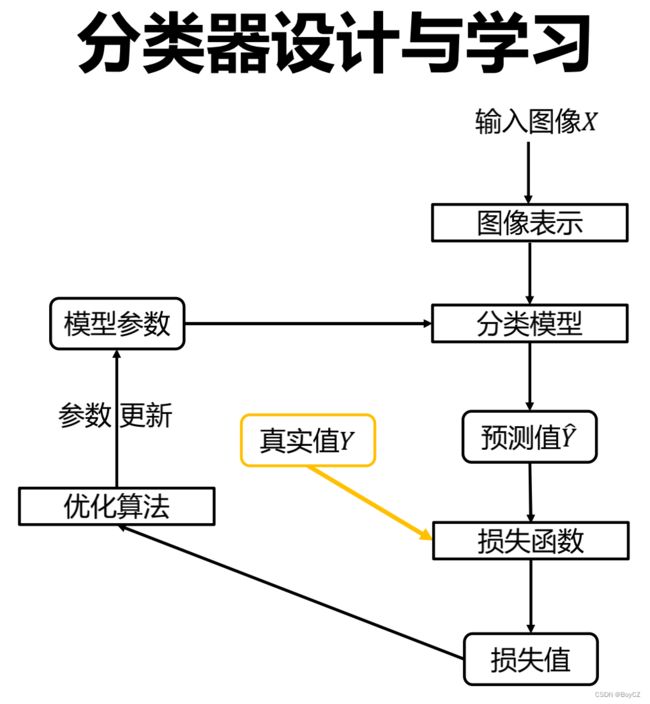
  我们的讲解顺序为图像表示、分类模型、预测值、损失函数、优化算法、数据集。

一、图像表示

  本段将介绍图像在计算机中的表示形式（基于像素的图像表示），以及图像如何输入到模型中。

基于像素的图像表示

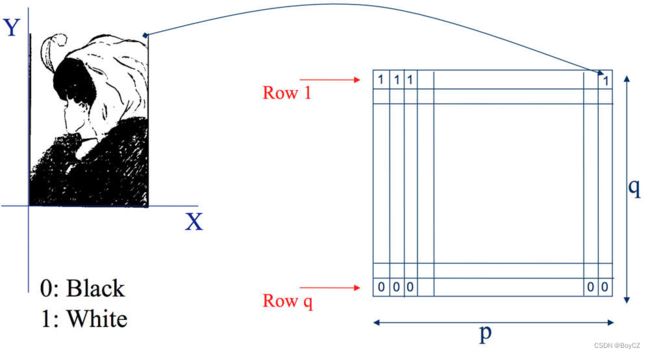
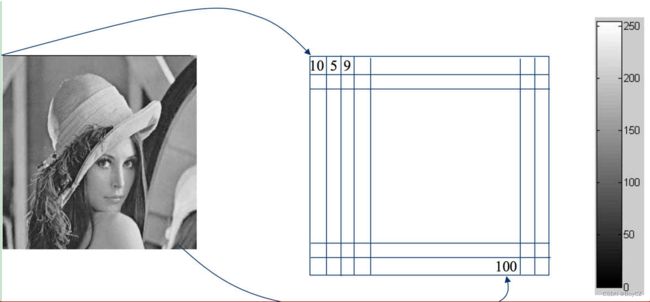
  图像分为三类：二进制图像（Binary）、灰度图（Gray Scale）、彩色图（Color）。

• 二进制图像：它的每一个像素点要么为1，要么为0，1代表白色而0代表黑色，所以整幅图像的像素点要么是白的要么是黑的。

• 灰度图：它的每一个像素点有一个取值范围，取值范围在[0,255]，数字越接近0，像素点越黑，越接近255，像素点越白。

• 彩色图：通常称为RGB图像（Red Green Blue），我们看到的RGB图像可以看成由三张图重叠在一起显示出来的，也就是三个通道，第一个通道也就是最上面一张图是全红的，第二通道的全绿，第三通道的全蓝，每一个通道的图像像素点取值也为[0,255]，0代表黑，255代表该通道的颜色（比如第一通道那么像素点的取值越接近255，该像素点越红）。
  知道了图像是基于像素的表示方法，那对于一幅图像，该如何输入到分类模型中呢？最简单的方法就是将图像矩阵转换为向量，比如对于一幅3X20X20（3个通道，高为20个像素点，宽也为20）的图像，我们可以将其拉成32020=1200个元素的矩阵：$x=[r_1,g_1,b_1,...,r_n,g_n,b_n]$，实际就是将彩色图像的第一个像素点的三个通道上的值$r_1$，$g_1$，$b_1$放在向量的前三个位置，然后将彩色图像第二个像素点的三个通道上的值$r_2$，$g_2$，$b_2$放在向量的第4、5、6个位置，以此类推一直到$r_n$，$g_n$，$b_n$。

分类模型

  这里我们用线性分类器来作为分类模型进行讲解。以下为后续会出现的符号含义，后面出现时还会再介绍。

符号	含义
$x$	输入的图像的向量，维度为$d$
$W$	权值向量
$b$	偏执向量
$c$	图像的类别个数
$y$	标签，图像的实际类别
$s_{ij}$	第$i$个样本第$j$个类别的输出分数

1. 线性分类器的定义

  线性分类器是一种线性映射，将输入的图像特征映射为类别分数。简单来说就是对输入图像$x$，通过一个线性函数$f(x)=Wx+b$ 计算出一个值作为其类别分数，其中$W$为权重或权值，$b$为偏执，$W$和$b$都是分类器帮我们确定出的值。假设我们现在有$c=10$个类（猫、狗、飞机、汽车…）的图像，那么第$i$个类的线性分类器可以设计成：
$$f_i(x,W_i)=W^{T}x+b_i,i=1,2,...,c\text{\hspace{1em}(1)}$$
对于$W$和$b$的维度我们暂时不研究，先把他们都想象成一个数就行，我们最终得到的$f_i(x,W_i)$就是第$i$个分类器对输入图像$x$进行计算后得到的数值，这个数值越大，代表图像$x$越有可能是$i$（比如猫）这个类。那我们最终如何确定$x$到底属于哪个类呢？这就需要我们把图像$x$输入到全部的$c$个分类器中，计算出$c$个数值，若第$i$个分类器计算出的数值比其他分类器的数值都要大，那么$x$就属于$i$类，实际计算中并不需要循环迭代计算$f_i(x,W_i)$，通过矩阵运算即可一次性计算所有类的输出值，这里是为了方便理解而已。例如下图：

我们j将上图拉伸为向量$x=[56,231,24,2]$，实际的向量肯定不是这样子，这里是为了演示。接下来我们将图像输入分类器进行计算：
这里我们只用了三个类来演示，可以看到，我们的$W^T=[W_1^T,W_2^T,W_3^T]$，其维度为（3,4），3是类别数，也就是$c=3$，4是图像向量$x$的维度，也就是$d$=4，偏执$b$也为向量，其维度为类别个数$c$，计算出$f=W^{T}x+b，f=[f_1,f_2,f_3]$，上图可以看出，$f_2$的值最高，所以最终分类器告诉我们$x$属于猫这个类。至于$W$和$b$的值是怎么得到的，后面再说。

2. 线性分类器的权值

  上面我们说的权值$W$，他的含义到底是什么呢？那让我们利益CIFAR10数据集（10个类，$c=10$）训练一个线性分类器，并拿出训练好的$W$看看到底它是什么，通过$f_i(x,W_i)=W^{T}x+b_i，i=1,2,...,c$ 可有计算出第$i$个类的$W_i，i=1,2,...,c$，我们把这10个$W_i$画出来看看：
我们可以看出$W_2$很想车头，$W_8$很像马，这个马有两个头，那是因为数据集中有些图片马头朝左，有些朝右。所以其实$W$就像是个模板，与这个模板长得越像，那么就把这个图像分为哪一类，原理就是$W$乘以$x$的时候，如果$W$与$x$长得越像，他们的积也越大。所以分类器要做的就是要确定出模板$W$,这样它才能做分类工作。至于如何得到$W$和$b$，这就需要损失函数和优化算法来帮忙了。

损失函数

1. 损失函数的定义

  损失函数是一个函数，用于度量给定分类器的预测值与真实值的不一致程度，其输出通常是一个非负实值，其输出的非负实值可以作为反馈信号来对分类器参数进行调整，以降低当前示例对应的损失值，提升分类器的分类效果。损失函数通常定义为：
$$L=\frac{1}{N}\underset{i}{\sum ^N}{L}_i(f(x_i,W),y_i)\text{\hspace{1em}(2)}$$
这里$N$为样本数量，$y_i$表示第$i$个样本的标签，$x_i$为第$i$个样本，$L_i$为第$i$个样本的损失函数，$L$是数据集的损失，他是数据集中所有样本损失的平均。

2. 多类支撑向量机损失

  上面讲述了损失函数的定义，那具体的$L_i$这个函数是如何定义的呢？我们定义$s_{ij}$为第$i$个样本第$j$个类别的输出分数，$j=1,2,...,c$，例如$s_{12}$就是第一个样本输入第2个分类器得到的分数。那么：
$$s_{ij}=f_j(x_i,W_j,b_j)=W_j^T{x}_i+b_j\text{\hspace{1em}(3)}$$
则第$i$个样本的多类支撑向量机损失定义如下（看不懂公式不急，下面有图）：
$$\begin{gathered} L_i=\sum _{j\ne y_i}\{\begin{array}{ll}0,& if{s}_{yi}\ge s_{ij}+1\\ s_{ij}+1-s_{y_i},& otherwise\end{array} \\ =\sum _{j\ne y_i}max(0,s_{ij}+1-s_{y_i})\text{\hspace{1em}(4)} \end{gathered}$$
$s_{y_i}$是指第$i$个样本在其真实分类器的预测分数，若样本是猫，那么他在狗这个分类器的输出值理应很小才对，也就是说一张图为猫，这张图在猫这个分类器的输出分数（$s_{y_i}$）大于这张图在其他分类器的输出分数（$s_{ij}$）加1，那么这张图就没有损失，分类器很好的将其判断为猫，也就是公示（4）中$if{s}_{y_i}\ge s_{ij}+1，L_i=0$ ，如果不满足上述所说的情况，这张图的$L_i$则为$s_{ij}+1-s_{y_i}$，因为前面说了损失都是非负值，所以这里是$s_{ij}+1-s_{y_i}$。如果到这里还没看懂也没事，下面方三张图作为例子，相信聪明的你看一下这个计算过程就明白了：


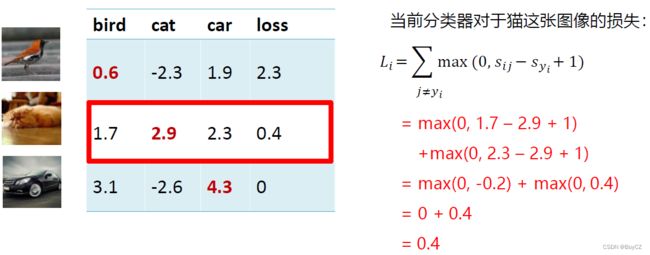
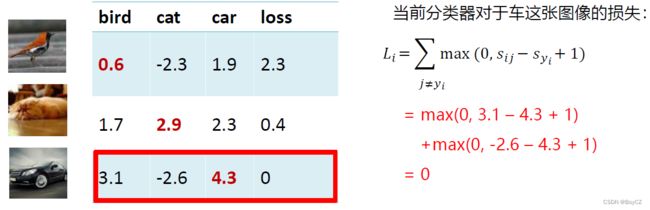
看完上面的例子，相信已经能够理解公示的含义。又回到最初的问题，损失函数知道了，那损失函数是如何帮助分类器确定权值$W$的呢？其实仅仅只靠损失函数还无法确定权值，但是至少知道损失函数了，我们就能确立我们的目标——让损失函数最小化，如果损失为0即没有损失，那不就代表着分类器对这个数据集是100%预测准确了，所以我们接下来要做的就是让损失接近0，等于0是不可能的。让损失接近0这个目标就交给优化算法来做，优化算法就是不断调整权值$W$，最开始的时候损失计算出来很大，优化算法帮我们更改一下$W$并重新计算损失使得损失变小，不断调整权值不断计算损失，当损失不再变小的时候，最终留下的这个权值就作为模板，这个稍后再细讲，我们先说正则项。

3. 正则项与超参数

  假设存在一个$W$使损失函数$L=0$，这个$W$是唯一的吗？当然是不唯一的，很有可能出现$2W$也能使得$L=0$。那我们是选择$W$好还是$2W$好呢？先说结论，$W$更好，因为$W$的数值更小，不容易守噪声影响，相反$2W$就很容易被影响，举个例子：对于样本$x=[1,1,1,1]$，分类器1：$W_1=[1,0,0,0]$，分类器2：$W_2=[0.25,0.25,0.25,0.25]$，两个分类器的输出:$W_1^{T}x=W_2^{T}x=1$，虽然他们输出一样，但是对于分类器2来说，它可以学习到样本的全部特征，而对于分类器1来说，因为它的权值中只有第一个元素为1其余为0，那么矩阵相乘的时候样本第一个特征能被学习到，而剩下三个特征因为乘以0直接没了，如果这时候样本的第一个特征刚好是个噪声（比如这个特征值为身高3米5），那么就会将分类器模型带偏。所以我们要使用分类器2，即使第一个特征是噪声，但其系数只有0.25，切分类器还能考虑到其他几个特征不至于被带得很偏。那么我们要怎样让分类器选择$W_2$呢？这就要引入正则项与超参数。

- 什么是正则项？

  先看一个公示：
$$L(W)=\frac{1}{N}\sum _i{L}_i(f(x_i,W),y_i)+\lambda R(W)\text{\hspace{1em}(5)}$$
 &emsp公式中的黑色部分是之前讲过的，红色部分即正则项，蓝色部分为超参数。红色部分的$R(W)$是一个与权值有
关，跟图像数据无关的函数,假设$W$的维度为$(k,l)$，那么$L_2$（这里的$L$不是损失函数）正则项：
$$R(W)=\sum _k\sum _l{W}_{kl}^2\text{\hspace{1em}(6)}$$
其实也就是$W$中所有元素的平方和，我们来看上面那个例子，分类器1：样本$x=[1,1,1,1]$，$W_1=[1,0,0,0]$，分类器2：$W_2=[0.25,0.25,0.25,0.25]$，输出：$W_1^{T}x=W_2^{T}x=1$，我们计算出$R(W_1)=1，R(W_2)=0.25$，那么对于公式（5）来说，损失$L(W_1)>L(W_2)$，那么模型自然会选择损失小的$W_2$，这就是正则项的作用：防止模型在数据集上学习得太好导致泛化能力差。L2正则损失对大数值权值进行惩罚，喜欢分散权值，鼓励分类器将所有维度的特征都用起来，而不是强烈的依赖其中少数几维特征。常用的正则项有：
$$\begin{gathered} L_1正则项：R(W)=\sum _k\sum _l|W_{kl}| \\ {L}_2正则项：R(W)=\sum _k\sum _l{W}_{kl}^2 \\ Elasticnet(L_1+L_2):R(W)=\sum _k\sum _l\beta W_{kl}^2+|W_{kl}| \end{gathered}$$

- 什么事超参数？

  至于超参数，是人为设置的一个参数，通过选择你觉得合适的参数来训练模型。下面还会再讲超参数。

优化算法

1. 什么是优化

  参数优化是机器学习的核心步骤之一，它利用损失函数的输出值作为反馈信号来调整分类器参数，以提升分类器对训练样本的预测性能。

2. 优化算法的目的是什么？

  上面大致提过，我们再来复习一遍：
  损失函数$L$（公式5）是一个与参数$W$有关的函数，优化的目标就是找到使损失函数$L$达到最优的那组参数$W$。一种直接的方法是求$\frac{\Delta L}{\Delta W}=0$，也就是求导找极值点，但是通常，$L$形式比较复杂，很难从这个等式直接求解出$W$。所以有了梯度下降算法，一种简单而高效的迭代优化方法！

3. 梯度下降算法

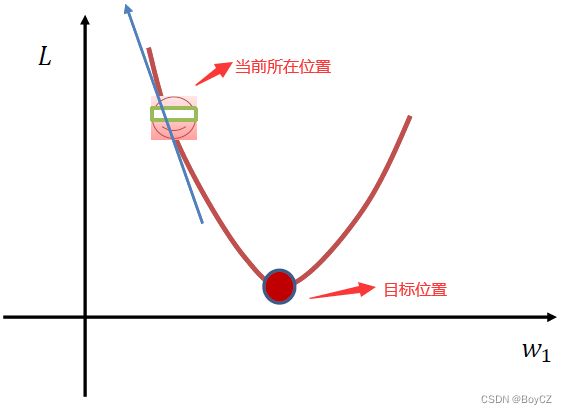
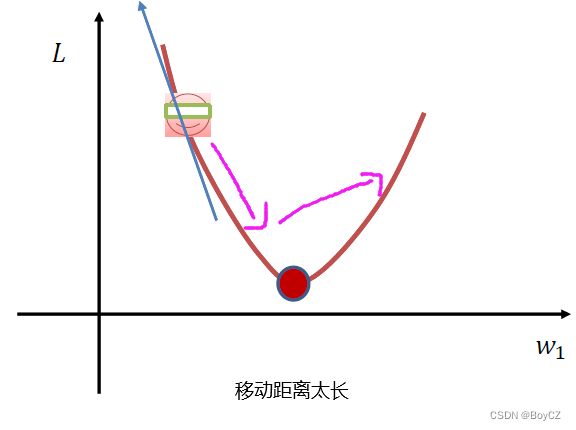
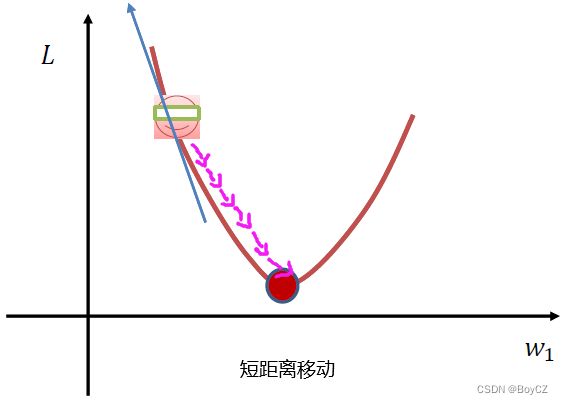
  我们看下面这张图，横坐标是权值，纵坐标是损失，假设当前的损失在如图所指位置，我们想让损失降到最低点该怎么做呢？我们从图中能看出$W_1$应该向右移动才能到达最低点，但是我们的模型并不知道，这幅图是假设的，其实包括我们也不知道最低点在哪儿。这时候就需要用梯度下降算法，我们求出当前所在位置的梯度（图中蓝色箭头），沿着梯度的反方向（也就是向右）走，那不就可以到达最低点了。但是具体要走多远呢，因为我们不知道最低点在哪儿，所以我们只能一小步一小步的走。走的距离太长就容易导致直接跨越最低点到最低点的右侧了。实习操作就是用当前的$W_1$减去梯度乘以学习率得到一个差值，这个差值再赋给权值即可，学习率也是一个超参数，人为指定，通常为0.001。我们再来理解一下，此图的$W_1$为正值，减去梯度乘以学习率（负值）则相当于权值加了一个正值，权值向右移动，为了防止移动的距离太长，所以我们让梯度乘以了一个小于1的学习率，使得移动的距离不要太长，我们不断地计算梯度，用计算出的梯度来移动权值，权值移动后重新计算损失，循环往复，直到损失不再下降（保持在一个范围内波动），则学习完毕。

while True:
		权值的梯度=计算梯度（损失，训练样本，权值）
		更新后的权值=当前权值-学习率*权值的梯度

  下面我们来看看梯度下降算法的计算效率：
刚才给出了梯度下降算法的伪代码，其中我们注意到更改权值前需要先计算出权值的梯度，而这里我们的输入是全部样本，意思是每次的while循环都需要计算所有样本的损失和梯度，这个计算量是很大的，当样本量很大的话，这将不堪重负，这导致梯度下降算法的效率并不高，那该如何解决这个问题呢？因此出现了随机梯度下降算法。

4. 随机梯度下降

  与梯度下降不同，随机梯度下降算法在计算损失和梯度时不适用全部的样本数据，而是随机选取一个样本计算权值的梯度，这大大的缩短了计算时间，但新的问题随之出现，单个样本的训练可能会带来很多噪声，不是每次迭代都向着整体最优化方向。为了解决这个问题，有了最合适的小批量随机梯度下降算法。

5. 小批量随机梯度下降

  小批量随机梯度下降就是在计算权值的梯度时，我们每次选取m个样本用来计算随时并更新梯度。如下所示：
$$\begin{gathered} L(W)=\frac{1}{m}\underset{i=1}{\sum ^m}{L}_i(x_i,y_i,W)+\lambda R(W) \\ \Delta {}_{W}L(W)=\frac{1}{m}\underset{i=1}{\sum ^m}\Delta {}_W{L}_I(x_i,y_i,W)+\lambda \Delta {}_{W}R(W) \end{gathered}$$
这里m叫批量大小，是超参数，通常为2的倍数，如16,32或128。这种算法即减少了计算实践，又降低了模型受到噪声干扰的影响。
一些术语：

• iteration：表示1次迭代，每次迭代更新1次网络结构的参数；
• batch-size：1次迭代所使用的样本量；
• epoch：1个epoch表示过了1遍训练集中的所有样本。

数据集

1. 数据集划分

我们通常将一个数据集划分为三部分：训练集、验证集、测试集。训练集用于给定的超参数（学习率、批量大小等）时分类器参数（权值和偏执）的学习。验证集用于帮助我们选择最佳的超参数，比如我们用训练集将模型训练好后，将模型作用于验证集中，若其效果较差说明模型泛化能力差，需要调整超参数。测试集我们要当做是不存在的，只有确定模型不再更改时才用来评估模型的能力。

2. 数据集预处理

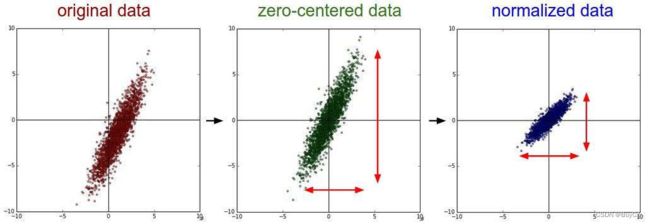  我们看上面三幅图，最左边的是原始数据，可以发现他在不同特征上表现出不同的取值差距，这样的数据是不适合用来训练的，比如我们通过身高和体重来区分男女，如果体重的单位使用吨，那么体重的数据值之间的差距将会非常小，对于模型来说，很难通过这个维度来区分男女，所以我们需要做归一化处理，归一化的原因还有很多，不再赘述。

I am BoyCZ，若您对我的文章表示认可，麻烦点个赞，欢迎关注我的知乎：BoyCZ