Dijkstra 地图导航查找最短路径算法,临接表 JavaScript实现
Dijkstra 最短路径-临接表算法使用用Map存储邻接表和结果表,运用了dijkstra算法会选择最短距离的路径来访问节点的特性查找到达目标节点的最短路径。
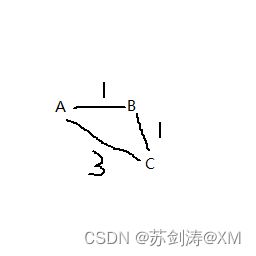
邻接表结构:
{a:[ // 顶点a有两个临接点:b,c
{dist:1,target:b},
{dist:3,target:c}
],
b:[
{dist:1,target:c}
]
}
以上邻接表带入方法得到到达b的最短路径是:a-b,长度1;到达c的最短路径是a-b-c,长度是 1+1 = 2;(a-c的长度是3)
算法描述:
1. new 一个结果Map,用于存放起点到各个点的距离和路径,要默认存放起点到起点的为访问数据,后续遍历邻接表时会把对应项可以到达的目标点先存放到该结果集,作为待访问点,用于后续对其结果数据的更新。
result结构:
[origin: { // 默认数据起点到起点,距离0,未访问
dist: 0, // 起点到该点的距离
visited: true, // true 表示该点结果已确认为最短路径,后续不会再发生更改
path: [] //起点到该点的路径
},
a:{
dist:1,
visited:false,
path:[]
}
]
2.开始遍历临接表,每次的操作是: 从result中找到最近的(dist最小的)待访问点(visited:false),最开始会找到起点到起点这个结果项:origin,然后将该结果集的访问结果设置true(已经确定没有其他任何路径能更短了。因为后续所有的距离计算都至少在这个距离上接着加,因为到达未访问的任意一点的距离都比到达当前点的距离长,那么从其他点折回该点自然更长),然后从邻接表中获取到这个节点的信息得到该节点的相邻节点。
3.对这些相邻节点进行遍历:记录相邻节点到结果集中,并判断从origin到达这些点的距离,如果比之前记录的到达这些点的距离更短则更新结果集中的数据。如:
原本在记录a的邻接点c的时候结果集保存的是:
c:{
dist:3,
visited:false,
path:[a,c]
}
后续从result中找到最近未访问的点b,再对b的临接点记录发现b到c的距离是1,而本来a到b的距离是1,这样a-b-c的距离就是1+1 = 2比原来的a-c距离小,于是更新结果集中的c是:
c:{
dist:2,
visited:false,
path:[a,b,c]
}
4.从代码上讲其实这里应该接到第2点后面,为了方便理解还是将结果判断放在最后:得到最近的未访问点后判断该点是否是目标点(即确定result中保存的到达该未访问点的最短路径就是到达目标点的最短路径)终止所有遍历,从result中获取该未访问点并返回
(例子中的顺序是记录a-b,a-c,访问b;如果b还有临接点d,且b-d距离是0.5,那么接下去记录b-d,和b-c,访问d,如果d还有邻接点,会先记录d的邻接点,因为起点到达d的距离是1.5,而到达c的距离是2;如果d能接到c,且d-c的距离是0.2,这时a-b-c的距离是2,但a-b-d-c的距离是1.7比2还要小,那么接下去result中找到最近的待访问点是c,到达c的路径数据是a-b-d-c。后续访问c的邻接节点从a-b-d-c出发累加。建议画图理解)
具体看代码
/**
* Dijkstra 最短路径-临接表算法
* @param {Map} table 邻接表{a:[{dist:1,target:b,path:path},
* {dist:2,target:c,path,points}]}
* @param {*} origin 起点
* @param {*} destination 终点
* @author Su Jiantao
*/
function dijkstra(table, origin, destination) {
let result = new Map() // 存放从起点到各个点的距离和路径
const { size } = table
result.set(origin, { // 默认数据起点到起点,距离0,未访问
dist: 0,
visited: false,
path: []
}) // 设置原点
for (let i = 0; i < size; i++) {
const near = minDistance(result) // 找到下个最近的节点的索引 第一次会找到origin自己
if (near === 'NO FOUND') break; // 无法到达下一个节点,则没有找到路径
const nearPoints = table.get(near) // 访问最近的点 第一次访问的是origin
const nearP = result.get(near)
nearP.visited = true // 把选出的顶点标true 防止重复计算
if (near === destination) break; // 已找到节点 如果不判断,result里会存放到达所有顶点的最短路径
nearPoints.forEach(e => {
let target = result.get(e.target)
if (!target) { // 目标点还未被记录
result.set(e.target, { // 记录该点
dist: INF,
visited: false,
path: []
})
target = result.get(e.target)
}
if (!target.visited // target节点未被访问
&& nearP.dist + e.dist < target.dist // 找到距离更短的路径到达e.target
) {
// 更新结果集中到达target的最短路径
target.dist = nearP.dist + e.dist
target.path = [].concat(nearP.path)
target.path.push({points:e.points,top:e.tip})
}
})
}
return result.get(destination)
}
/**
* 找到最近一个没有访问过的节点
* @param {Map} result
* @returns
*/
function minDistance(result) {
let min = INF
let minIndex = 'NO FOUND';
result.forEach((e, p) => {
if (e.dist < min && !e.visited) {
min = e
minIndex = p
}
})
return minIndex
}