内插散点数据
目录
散点数据
使用 griddata 和 griddatan 插入散点数据
scatteredInterpolant 类
使用 scatteredInterpolant 类插入散点数据
复数散点数据的插值
解决散点数据插值中的问题
散点数据
散点数据包含点集X和对应值V,其中的点没有结构或其相对位置间的顺序。进行散点数据插值有多种方法。一种广泛使用的方法是使用点的 Delaunay 三角剖分。
此示例说明如何通过对点进行三角剖分并按模V将顶点提升至与X正交的维度,来构建插值曲面。
应用此方法有多种方式。在本示例中,插值分为几个单独的步骤;通常情况下,整个插值过程通过一次函数调用完成。在抛物面上创建散点数据集。
X = [-1.5 3.2; 1.8 3.3; -3.7 1.5; -1.5 1.3; ...
0.8 1.2; 3.3 1.5; -4.0 -1.0; -2.3 -0.7;
0 -0.5; 2.0 -1.5; 3.7 -0.8; -3.5 -2.9; ...
-0.9 -3.9; 2.0 -3.5; 3.5 -2.25];
V = X(:,1).^2 + X(:,2).^2;
hold on
plot3(X(:,1),X(:,2),zeros(15,1), '*r')
axis([-4, 4, -4, 4, 0, 25]);
grid
stem3(X(:,1),X(:,2),V,'^','fill')
hold off
view(322.5, 30);如图所示:
创建 Delaunay 三角剖分,提升顶点,并在查询点 Xq 位置计算插值。
figure('Color', 'white')
t = delaunay(X(:,1),X(:,2));
hold on
trimesh(t,X(:,1),X(:,2), zeros(15,1), ...
'EdgeColor','r', 'FaceColor','none')
defaultFaceColor = [0.6875 0.8750 0.8984];
trisurf(t,X(:,1),X(:,2), V, 'FaceColor', ...
defaultFaceColor, 'FaceAlpha',0.9);
plot3(X(:,1),X(:,2),zeros(15,1), '*r')
axis([-4, 4, -4, 4, 0, 25]);
grid
plot3(-2.6,-2.6,0,'*b','LineWidth', 1.6)
plot3([-2.6 -2.6]',[-2.6 -2.6]',[0 13.52]','-b','LineWidth',1.6)
hold off
view(322.5, 30);
text(-2.0, -2.6, 'Xq', 'FontWeight', 'bold', ...
'HorizontalAlignment','center', 'BackgroundColor', 'none');如图所示:
此步骤通常涉及遍历三角剖分数据结构体以求包围查询点的三角形。找到该点之后,计算值的后续步骤取决于插值方法。可以计算相邻的最近的点,并使用该点的值(最近邻插值方法)。也可以计算包围三角形的三个顶点值的加权和(线性插值方法)。有关散点数据插值的文本和参考资料中介绍了这些方法及其变化形式。
尽管这里主要说明二维插值,但此方法也可应用于更高的维度。更一般的描述是,给定点集 X 和对应的值 V,可以构造 V = F(X) 形式的插值。您可以在查询点 Xq 计算插值,即
Vq = F(Xq)。这是一个单值函数;对于 X 的凸包中的任何查询点 Xq,它将产生唯一的值 Vq。为了产生满意的插值,假定样本数据适用此属性。
MATLAB® 提供两种方式执行基于三角剖分的散点数据插值:
-
函数 griddata 和 griddatan
-
scatteredInterpolant 类
griddata 函数支持二维散点数据插值。griddatan 函数支持 N 维散点数据插值;但是对于高于六维的中到大型点集并不实际,因为基本三角剖分需要的内存呈指数增长。
scatteredInterpolant 类支持二维和三维空间中的散点数据插值。鼓励使用这种类,因为它的效率更高,容易适应更广泛的插值问题。
使用 griddata 和 griddatan 插入散点数据
griddata griddata和 griddatan 函数接受一组样本点 X、对应值 V 和查询点 Xq,然后返回插入的值 Vq。这两个函数的调用语法类似,主要区别在于二维/三维 griddata 函数可依据 X, Y / X, Y, Z 坐标来定义点。这两个函数在预定义的网格点位置插入散点数据,意图是产生网格数据,因此得名。在实际中插值的使用更具一般性。也许需要在点的凸包内的任意位置进行查询。
此示例说明 griddata 函数如何在一系列网格点进行散点数据插值,并使用此网格数据创建等高线图。
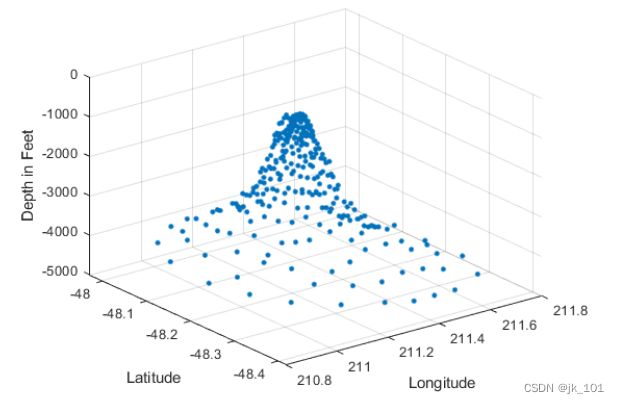
绘制 seamount 数据集(海底山是指水下山脉)。该数据集包含一组经度 (x) 和纬度 (y) 位置,以及在这些坐标位置测量的对应 seamount 海拔 (z)。
load seamount
plot3(x,y,z,'.','markersize',12)
xlabel('Longitude')
ylabel('Latitude')
zlabel('Depth in Feet')
grid on如图所示:
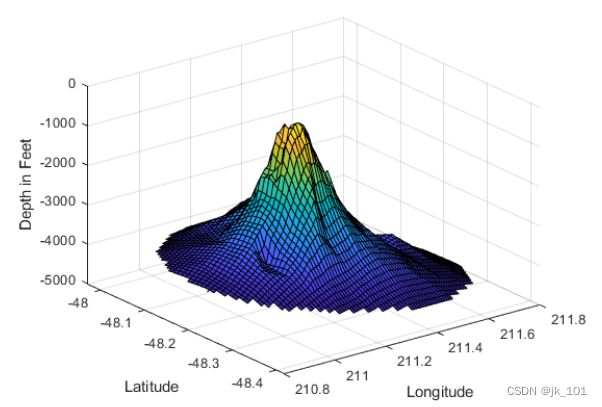
使用 meshgrid 在经度-纬度平面创建一组二维网格点,然后使用 griddata 在这些点插入对应的深度。
figure
[xi,yi] = meshgrid(210.8:0.01:211.8, -48.5:0.01:-47.9);
zi = griddata(x,y,z,xi,yi);
surf(xi,yi,zi);
xlabel('Longitude')
ylabel('Latitude')
zlabel('Depth in Feet')如图所示:
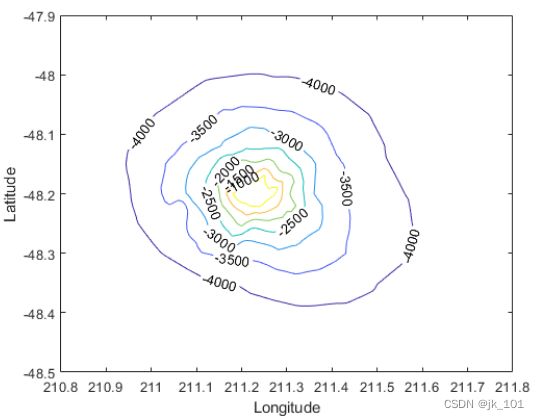
现在,数据已转换为网格化格式,计算并绘制等高线。
figure
[c,h] = contour(xi,yi,zi);
clabel(c,h);
xlabel('Longitude')
ylabel('Latitude')如图所示:
也可以使用 griddata 在数据集的凸包中任意位置处进行插值。例如,坐标 (211.3, -48.2) 处的深度由以下值给出:
zi = griddata(x,y,z, 211.3, -48.2);每次调用 griddata 函数时都会计算基本三角剖分。如果用不同的查询点对相同的数据集重复进行插值,这样可能会影响性能。使用 scatteredInterpolant 类插入散点数据中描述的 scatteredInterpolant 类在这方面效率更高。
MATLAB 软件还提供了 griddatan 以支持更高维的插值。调用语法类似于 griddata。
scatteredInterpolant 类
在需要通过插值对一组预定义网格点位置求值时,griddata 函数可派上用场。实际上,插值问题往往更普遍,scatteredInterpolant 类的灵活性更强。这个类具有以下优点:
-
它引入了可高效查询的插值函数。即基本三角剖分只创建一次,然后在后续查询中重复使用。
-
可改变插值方法,与三角剖分无关。
-
数据点处的值也可更改,与三角剖分无关。
-
数据点可被逐步添加到现有插值中,无需触发整个重算过程。相对于样本点总数而言,如果要编辑的点数较少,那么数据点的删除和移动效率很高。
-
对于凸包外部的点,提供了外插功能以求得近似值。
scatteredInterpolant 提供以下插值方法:
-
'nearest' - 最近邻点插值,其中的插值曲面是不连续的。
-
'linear' - 线性插值(默认值),其中的插值曲面是 C0 连续的。
-
'natural' - 自然邻点插值,其中的插值曲面是 C1 连续的,但样本点除外。
scatteredInterpolant 类支持二维和三维空间中的散点数据插值。可以通过调用 scatteredInterpolant,传递插值点位置和对应值,并使用内插和外插方法作为可选参数,来创建插值。
使用 scatteredInterpolant 类插入散点数据
本示例显示如何使用 scatteredInterpolant 插入 peaks 函数的散点样本。
创建散点数据集。
rng default;
X = -3 + 6.*rand([250 2]);
V = peaks(X(:,1),X(:,2));创建插值
F = scatteredInterpolant(X,V)
F =
scatteredInterpolant with properties:
Points: [250x2 double]
Values: [250x1 double]
Method: 'linear'
ExtrapolationMethod: 'linear'Points 属性表示数据点的坐标,Values 属性表示关联值。Method 属性表示执行插值的插值方法。ExtrapolationMethod 属性表示当查询点位于凸包外部时使用的外插方法。
按照访问 struct 的字段的相同方式访问 F 的属性。例如,使用 F.Points 检查数据点的坐标。
求出插值
scatteredInterpolant 可以按下标方式求某点的插值。其求值方式与函数相同。可以按如下方式求出插入的值。这种情况下,位于查询位置的值由 Vq 给出。可以对单个查询点求值:
Vq = F([1.5 1.25])
Vq = 1.4838可以求单个坐标:
Vq = F(1.5, 1.25)
Vq = 1.4838可以在点位置向量处求值:
Xq = [0.5 0.25; 0.75 0.35; 1.25 0.85];
Vq = F(Xq)
Vq = 3×1
0.4057
1.2199
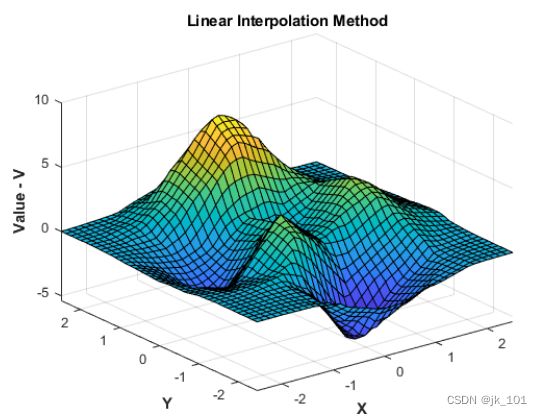
2.1639可以计算网格点位置的F并绘制结果。
[Xq,Yq] = meshgrid(-2.5:0.125:2.5);
Vq = F(Xq,Yq);
surf(Xq,Yq,Vq);
xlabel('X','fontweight','b'), ylabel('Y','fontweight','b');
zlabel('Value - V','fontweight','b');
title('Linear Interpolation Method','fontweight','b');如图所示:
更改插值方法
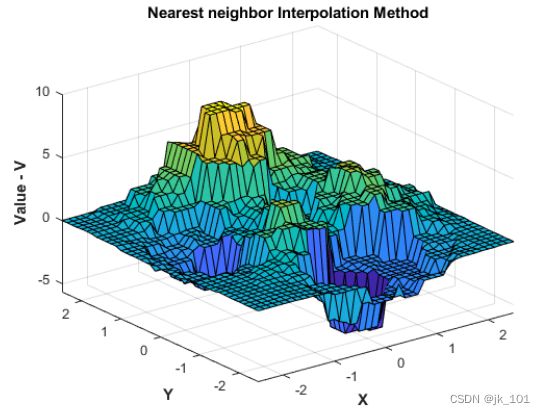
可以动态更改插值方法。将方法设置为 'nearest'。
F.Method = 'nearest';按以前方式重新计算并绘制插值。
Vq = F(Xq,Yq);
figure
surf(Xq,Yq,Vq);
xlabel('X','fontweight','b'),ylabel('Y','fontweight','b')
zlabel('Value - V','fontweight','b')
title('Nearest neighbor Interpolation Method','fontweight','b');如图所示:
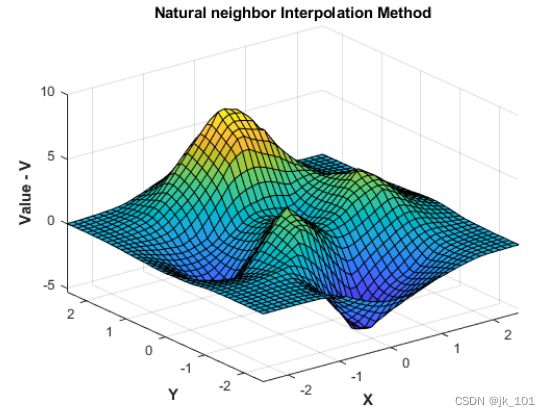
将插值方法更改为自然邻点,重新计算并绘制结果。
F.Method = 'natural';
Vq = F(Xq,Yq);
figure
surf(Xq,Yq,Vq);
xlabel('X','fontweight','b'),ylabel('Y','fontweight','b')
zlabel('Value - V','fontweight','b')
title('Natural neighbor Interpolation Method','fontweight','b');如图所示:
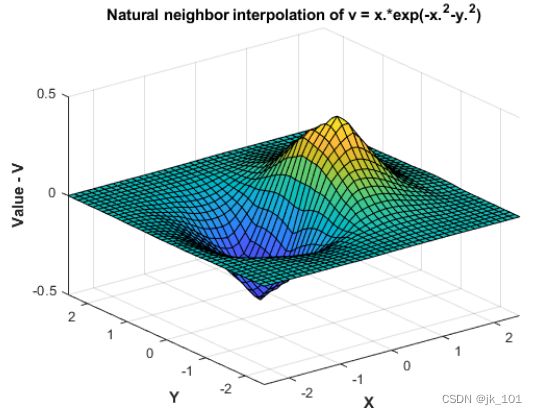
替换样本数据位置处的值。
可以动态更改位于样本数据位置 X 处的值 V。这在实际操作中很有用,因为一些插值问题可能在同一位置处具有多组值。例如,假设要为一个由位置 (x,y,z) 和对应的分量速度向量 (Vx,Vy, Vz) 定义的三维速度场进行插值。通过依次将每个速度分量赋给值属性 (V),可以进行插值。此方法具有重要的性能优点,因为它允许重复使用相同的插值,而不会引起每次计算新值的开销。
V = X(:,1).*exp(-X(:,1).^2-X(:,2).^2);
F.Values = V;求出插值并绘出结果。
Vq = F(Xq,Yq);
figure
surf(Xq,Yq,Vq);
xlabel('X','fontweight','b'), ylabel('Y','fontweight','b')
zlabel('Value - V','fontweight','b')
title('Natural neighbor interpolation of v = x.*exp(-x.^2-y.^2)')如图所示:
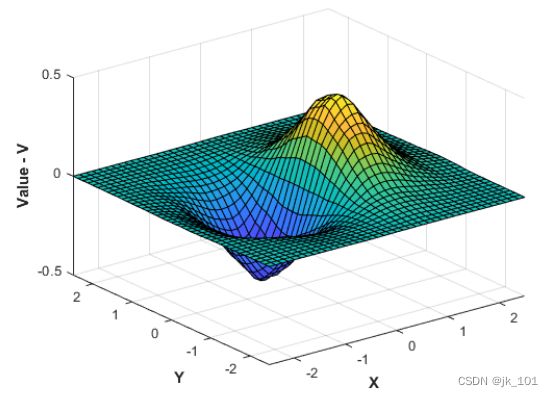
向现有插值添加其他点位置和值。
与使用扩充数据集完全重新计算相比,此方法可执行有效的更新。
在添加样本数据时,同时添加点位置和对应值很重要。
沿用该示例,按如下方式创建新样本点:
X = -1.5 + 3.*rand(100,2);
V = X(:,1).*exp(-X(:,1).^2-X(:,2).^2);给三角剖分添加新点和对应值。
F.Points(end+(1:100),:) = X;
F.Values(end+(1:100)) = V;求出改进的插值并绘出结果。
Vq = F(Xq,Yq);
figure
surf(Xq,Yq,Vq);
xlabel('X','fontweight','b'), ylabel('Y','fontweight','b');
zlabel('Value - V','fontweight','b');如图所示:
从插值中移除数据。
可以从插值逐步移除样本数据点。也可以从插值移除数据点和对应值。这对移除虚假离群值很有用。
在移除样本数据时,同时移除点位置和对应值很重要。
移除第 25 个点。
F.Points(25,:) = [];
F.Values(25) = [];移除第 5 至 15 个点。
F.Points(5:15,:) = [];
F.Values(5:15) = [];保留 150 个点,移除其余点。
F.Points(150:end,:) = [];
F.Values(150:end) = [];在求值和绘图时,这将创建一个粗略的曲面图:
Vq = F(Xq,Yq);
figure
surf(Xq,Yq,Vq);
xlabel('X','fontweight','b'), ylabel('Y','fontweight','b');
zlabel('Value - V','fontweight','b');
title('Interpolation of v = x.*exp(-x.^2-y.^2) with sample points removed')如图所示:
复数散点数据的插值
此示例说明如何在每个样本位置的值是复数时插入散点数据。
创建样本数据。
rng('default')
X = -3 + 6*rand([250 2]);
V = complex(X(:,1).*X(:,2), X(:,1).^2 + X(:,2).^2);创建插值。
F = scatteredInterpolant(X,V);创建网格查询点,求出网格点处的插值。
[Xq,Yq] = meshgrid(-2.5:0.125:2.5);
Vq = F(Xq,Yq);绘出 Vq 的实部。
VqReal = real(Vq);
figure
surf(Xq,Yq,VqReal);
xlabel('X');
ylabel('Y');
zlabel('Real Value - V');
title('Real Component of Interpolated Value');如图所示:
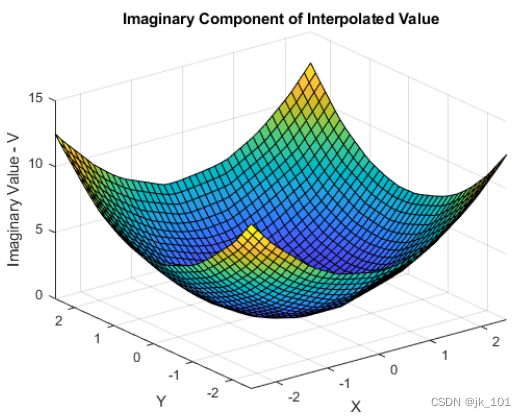
绘出 Vq 的虚部。
VqImag = imag(Vq);
figure
surf(Xq,Yq,VqImag);
xlabel('X');
ylabel('Y');
zlabel('Imaginary Value - V');
title('Imaginary Component of Interpolated Value');如图所示:
解决散点数据插值中的问题
前面部分中说明的许多示例处理的是在平滑曲面上采样的点集的插值。而且这些点的间距相对均匀。例如,点簇之间距离相对来说不大。此外,在点位置的凸包中插值求值情况良好。
在处理现实世界的插值问题时,数据可能更有挑战性。数据可能是从测量设备获取的,这些设备的读数可能不准确或者给出的是离群值。基础数据的变化可能不平滑,数值可能从点到点急剧跳跃。本节为您识别并解决散点数据插值的问题提供一些指导。
输入含有 NaN 的数据
应预处理含有 NaN 值的样本数据,以移除 NaN 值,因为此数据对插值没有作用。如果移除 NaN 后,还应移除对应的数据值/坐标,以确保一致。如果样本数据中存在 NaN 值,则在调用构建函数时会出错。
下面的示例说明如何移除 NaN。创建一些数据,然后用 NaN 替换一些项:
x = rand(25,1)*4-2;
y = rand(25,1)*4-2;
V = x.^2 + y.^2;
x(5) = NaN; x(10) = NaN; y(12) = NaN; V(14) = NaN;这段代码出错:
F = scatteredInterpolant(x,y,V); 正确的做法是,找出 NaN 的样本点索引后再构造插值:
nan_flags = isnan(x) | isnan(y) | isnan(V);
x(nan_flags) = [];
y(nan_flags) = [];
V(nan_flags) = [];
F = scatteredInterpolant(x,y,V);如果点位置属于矩阵形式,则下面的示例是相似的。首先,创建数据,用 NaN 替换一些项。
X = rand(25,2)*4-2;
V = X(:,1).^2 + X(:,2).^2;
X(5,1) = NaN; X(10,1) = NaN; X(12,2) = NaN; V(14) = NaN;这段代码出错:
F = scatteredInterpolant(X,V);找出 NaN 的样本点索引,然后构造插值:
nan_flags = isnan(X(:,1)) | isnan(X(:,2)) | isnan(V);
X(nan_flags,:) = [];
V(nan_flags) = [];
F = scatteredInterpolant(X,V);插值输出 NaN 值
当使用 'linear' 或 'natural' 方法查询凸包外部的点时,griddata 和 griddatan 返回 NaN 值。但是,如果使用 'nearest' 方法查询相同的点,可能会得到数值结果。这是因为凸包内部和外部都存在查询点的最近邻点。
如果要计算凸包外部的近似值,应使用 scatteredInterpolant。
重复点位置的处理
输入数据很少“十全十美”,应用程序不得不处理重复的数据点位置。数据集中位于相同位置的两个或多个数据点可能有不同的对应值。这种情况下,scatteredInterpolant 合并这些点,计算对应值的平均值。此示例说明 scatteredInterpolant 如何在具有重复点的数据集上执行插值。
-
创建位于平面上的一些样本数据:
x = rand(100,1)*6-3; y = rand(100,1)*6-3; V = x + y; -
通过将点 50 的坐标赋给点 100 产生一个重复的点位置:
x(50) = x(100); y(50) = y(100); -
创建插值。请注意,
F含有 99 个唯一数据点:F = scatteredInterpolant(x,y,V) -
检查与第 50 个点相关联的值:
F.Values(50)
这个值是第 50 和第 100 个原始值的平均值,因为这两个数据点位于同一位置:
(V(50)+V(100))/2这种情形下,插值以合理的方式解决模棱两可的情况。但是在某些实例中,数据点可能很靠近而不是完全一致,这些位置中的值可能不同。
在有些插值问题中,多组样本值可能对应于同一位置。例如,可在不同时间段记录同一位置的一组值。为提高效率,可以插入一组读数,然后替换数值,以插入下一组读数。
在存在重复点位置的情况下替换值时,始终使用一致的数据管理。假定有两组值与 100 个数据点位置相关联,希望通过替换数值依次插入每一组。
-
考虑这两组值:
V1 = x + 4*y; V2 = 3*x + 5*y -
创建插值。scatteredInterpolant 合并重复位置,插值含有 99 个唯一采样点:
通过 F.Values = V2 直接替换数值意味着将 100 个值赋给 99 个样本。由于前面合并操作的上下文已经丢失,样本位置的数量将与样本值的数量不符。消除这种不一致后才能对插值进行查询。F = scatteredInterpolant(x,y,V1)
在这种更复杂的情形中,需要移除重复项后才创建和编辑插值。使用 unique 函数求出唯一点的索引。unique 也可以输出标识重复点索引的参数。
[~, I, ~] = unique([x y],'first','rows');
I = sort(I);
x = x(I);
y = y(I);
V1 = V1(I);
V2 = V2(I);
F = scatteredInterpolant(x,y,V1) 现在可以使用 F 对第一个数据集进行插值。然后替换数值,对第二个数据集进行插值。
F.Values = V2;在编辑 scatteredInterpolant 时提高效率
scatteredInterpolant 允许编辑表示样本值的属性 (F.Values) 和表示插值方法的属性 (F.Method)。由于这些属性与基本三角剖分无关,因此可以高效率地执行编辑。但是,与使用大型数组一样,在编辑数据时应当小心谨慎,以免意外创建不必要的副本。若多个变量引用了同一个数组,然后该数组又被编辑过,在这种情况下就会产生副本。
在以下情况不会产生副本:
A1 = magic(4)
A1(4,4) = 11但是下面这种情况就会产生副本,因为该数组已被另一个变量引用。在进行编辑后,数组 A1 和 A2 就无法再共享同一个数据:
A1 = magic(4)
A2 = A1
A1(4,4) = 32同样,如果将数组传递给函数,然后在该函数中编辑此数组,则可能会发生深拷贝,具体取决于数据的管理方式。scatteredInterpolant 含有数据,其表现类似 MATLAB 语言中的数组,称为值对象。当应用程序按照文件中的函数这种方式组织时,MATLAB 语言能发挥最佳性能。在命令行进行原型构建可能达不到同样的性能水平。
下面的示例说明这种行为,但是应当注意到,本例中性能的提高不会推广到 MATLAB 中的其他函数。
这段代码不会产生最佳性能:
x = rand(1000000,1)*4-2;
y = rand(1000000,1)*4-2;
z = x.*exp(-x.^2-y.^2);
tic; F = scatteredInterpolant(x,y,z); toc
tic; F.Values = 2*z; toc可以将代码放入函数文件中,以更加高效率地执行。
如果程序是由文件中的函数组成的,那么 MATLAB 可以获得代码执行的整体情况;这就使 MATLAB 可以优化性能。在命令行上键入代码时,MATLAB 无法预料在下一步将键入什么内容,因此无法实现相同的优化水平。通过创建可重用的函数开发应用程序是通用惯例,并且建议这样做,MATLAB 将优化此设置中的性能。
凸包附近的插值结果效果不佳
Delaunay 三角剖分非常适合散点数据插值问题,因为它有优越的几何属性可产生良好的结果。这些属性是:
-
拒绝条形三角形/四面体,支持更多等边等面形体。
-
空外接圆属性,隐含地定义了点之间的最近邻关系。
空外接圆属性确保插入的值受查询位置的邻点中样本点的影响。尽管有这些特性,在某些情形中数据点的分布可能导致结果不良,在样本数据集的凸包附近通常发生这种情况。当插值产生意外结果时,通过绘制样本数据和基本三角剖分图常常能够深入了解问题。
本示例显示内插表面在边界附近退化。创建一个展示边界附近问题的示例数据集。
t = 0.4*pi:0.02:0.6*pi;
x1 = cos(t)';
y1 = sin(t)'-1.02;
x2 = x1;
y2 = y1*(-1);
x3 = linspace(-0.3,0.3,16)';
y3 = zeros(16,1);
x = [x1;x2;x3];
y = [y1;y2;y3]; 现在将这些样本点提升到曲面![]() 上,然后对曲面进行插值。
上,然后对曲面进行插值。
z = x.^2 + y.^2;
F = scatteredInterpolant(x,y,z);
[xi,yi] = meshgrid(-0.3:.02:0.3, -0.0688:0.01:0.0688);
zi = F(xi,yi);
mesh(xi,yi,zi)
xlabel('X','fontweight','b'), ylabel('Y','fontweight','b')
zlabel('Value - V','fontweight','b')
title('Interpolated Surface');如图所示:
实际曲面是:
zi = xi.^2 + yi.^2;
figure
mesh(xi,yi,zi)
title('Actual Surface')如图所示:
要了解插值曲面在边界附近退化的原因,着眼于基本三角剖分会有帮助作用:
dt = delaunayTriangulation(x,y);
figure
plot(x,y,'*r')
axis equal
hold on
triplot(dt)
plot(x1,y1,'-r')
plot(x2,y2,'-r')
title('Triangulation Used to Create the Interpolant')
hold off如图所示:
红色边界内的三角形形状相对良好,它们是根据附近邻域中的点构建的,此区域中的插值情况良好。在红色边界以外,三角形变成类似长条形,连接互相相隔很远的点。没有可精确捕获曲面的充分采样,因此这些区域中的结果不良不足为怪。在三维空间中,目测三角剖分变得更为复杂,但是了解点的分布情况常常有助于说明潜在问题。
MATLAB® 4 griddata 方法 'v4' 不是基于三角剖分的方法,也不会受到插值曲面在边界附近退化的影响。
[xi,yi] = meshgrid(-0.3:.02:0.3, -0.0688:0.01:0.0688);
zi = griddata(x,y,z,xi,yi,'v4');
mesh(xi,yi,zi)
xlabel('X','fontweight','b'), ylabel('Y','fontweight','b')
zlabel('Value - V','fontweight','b')
title('Interpolated surface from griddata with v4 method','fontweight','b');如图所示:
用 'v4' 方法调用 griddata 得到的插值曲面与预期的实际曲面相符。