day08-----pytorch
文章目录
- url:https://download.csdn.net/download/qq_34405401/12227750
- 1.深度学习介绍
- 2.常见神经网络结构介绍
-
- 2.1 前馈神经网络
- 2.2 反馈神经网络
- 2.3 图网络
- 3.深度学习框架
- 4.PyTorch
-
- 4.1 Storage 和 Tensor
- 4.2 自动求导--->优化器(优化器的梯度更新)
-
- 例1:使用导数求最小值
- 例2:使用导数实现线性回归
- 例3:使用导数实现LeNet-5卷积神经网络,完成手写数字识别
- 5.作业
-
- 5.1 作业1:
- 5.2 作业2:
url:https://download.csdn.net/download/qq_34405401/12227750
1.深度学习介绍
-
任何函数的模拟都可以使用多层神经网络逼近
-
深度学习特点
- 可以实现任何非线性的分类与预测
- 通过激活函数使线性向下一层传递时候变得非线性
-
单层神经网络叫感知器
-
通过线性运算(加权运算)进行网络结构设计(特征融合/特征分割)
-
最小化损失函数
- 梯度下降
- 导数的加减判定(极值点的方向)
- 加减的增量值(极值点的速度)
- x i = x i − 1 − η Δ x i − 1 x_{i} = x_{i-1} - \eta \Delta_{x_{i-1}} xi=xi−1−ηΔxi−1
- 怎么结束:固定步数或导数=0(梯度消失)或导数小于某个值
- 不使用所有样本计算,而使用一个样本或随机n个样本,即随机梯度下降
- 梯度下降
2.常见神经网络结构介绍
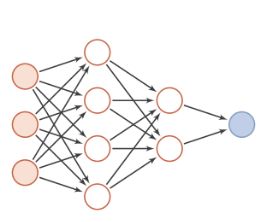
2.1 前馈神经网络
在前馈神经网络(Feedforward Neural Network, FNN )中,每一层的神经元可以接收前一层神经元的信号,并产生信号输出到下一层。第0层叫做输入层,最后一层叫做输出层,其他中间层叫做隐藏层。信号从输入层向输出层单向传播,可用一个有向无环图表示。
输入:向量或向量序列
包括:全连接前馈神经网络,卷积神经网络
表示:有向无环图
信息传播:朝着一个方向
BP神经网络:是一种按照误差逆向传播算法训练的多层前馈神经网络。
BP基本原理是:
利用前向传播最后输出的结果来计算误差的偏导数,再用这个偏导数和前面的隐藏层进行加权求和,如此一层一层的向后传下去,直到输入层(不计算输入层),最后利用每个节点求出的偏导数来更新权重。
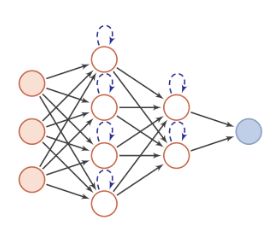
2.2 反馈神经网络
反馈神经网络中神经元不但可以接收其他神经元的信号,而且可以接收自己的反馈信号。和前馈神经网络相比,反馈神经网络中的神经元具有记忆功能,在不同时刻具有不同的状态。反馈神经网络中的信息传播可以是单向也可以是双向传播,因此可以用一个有向循环图或者无向图来表示。
常见的反馈神经网络包括循环神经网络、Hopfield网络和玻尔兹曼机。
输入:向量或向量序列
包括:循环神经网络,Hopfieid网络,波尔兹曼机
表示:有向循环图或者无向图
信息传播:可单向,可双向,可以自己到自己
神经元:有记忆功能,在不同时刻有不同状态。
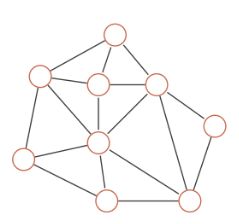
2.3 图网络
前馈神经网络和反馈神经网络的输入都可表示为向量或者向量序列,但实际应用中很多数据都是图结构的数据,比如知识图谱、社交网络和分子网络等。这时就需要用到图网络来进行处理。
图网络是定义在图结构数据上的神经网络,图中每个结点都由一个或者一组神经元组成。结点之前的连接可以是有向的,也可以是无向的。每个结点可以收到来自相邻结点或自身的信息。
输入:图结构数据(如:知识图谱,社交网络,分子网络等)
表示:可有向,可无向
信息传播:相邻节点或自己
结点:一个或一组神经元
3.深度学习框架
1.框架的关键点
- 神经层的类型(运算)
- 激活函数
- 损失函数的选择(选择不恰当会出现梯度消失、梯度暴躁)
- 优化器的选择以及优化器的学习率
2.常用框架
- Tensorflow
- PyTorch
- MaxNet
4.PyTorch
4.1 Storage 和 Tensor
构造Tensor(张量)是因为要求导,而矩阵或其他的数据类型是没办法求导的
import torch
#构造张量
t1=torch.Tensor()#注意此处T为大写
print(t1)
tensor([])
1.Tensor的标准构造
- Storage---->Tensor
#分配了五个空间
s1=torch.Storage(5)
s2=torch.Tensor(s1)
print(s2)
tensor([9.0919e-39, 8.9082e-39, 9.2755e-39, 8.4490e-39, 1.0194e-38])
2.常用的构造习惯:使用tensor()#注意此处t为大写
- 使用方法构造对象(可以把Python数据类型、Numpy转换为Tensor)
python转tensor:
t=torch.tensor(2)
print(t)
tensor(2)
t=torch.tensor(
[
[1,2,3],
[4,5,6]
]
)
print(t)
tensor([[1, 2, 3],
[4, 5, 6]])
numpy转tensor:
import numpy as np
arr=np.array([1,2,3,4])
t=torch.tensor(arr)
print(t)
tensor([1, 2, 3, 4], dtype=torch.int32)
3.Tensor属性:t.T
t=torch.tensor([[1,2,3],[4,5,6]])
print("t:",t)
print("转置:",t.T)
print("数据:",t.data)
print("取数据(推荐此种方法):",t.detach())#detach()与data区别:https://blog.csdn.net/dss_dssssd/article/details/89526623
print("类型:",t.dtype)
print("梯度函数:",t.grad_fn)#因为此处没参与运算,没绑定
print("梯度:",t.grad)#因此此处没参与运算,没绑定
print("求导状态:",t.requires_grad)
t: tensor([[1, 2, 3],
[4, 5, 6]])
转置: tensor([[1, 4],
[2, 5],
[3, 6]])
数据: tensor([[1, 2, 3],
[4, 5, 6]])
取数据(推荐此种方法): tensor([[1, 2, 3],
[4, 5, 6]])
类型: torch.int64
梯度函数: None
梯度: None
求导状态: False
4.Tensor的自动跟踪
t1=torch.tensor([1.0])
t2=torch.tensor([2.0])
t3=t1+t2
print(t3.detach().data,t3.grad_fn,t1.requires_grad,t2.requires_grad)
tensor([3.]) None False False
t1.requires_grad,t2.requires_grad=True,True
t4=t1+t2
print(t4)
tensor([3.], grad_fn=)
4.2 自动求导—>优化器(优化器的梯度更新)
例1:使用导数求最小值
- y = x 2 − 2 x + 5 y=x^2-2x+5 y=x2−2x+5
1.自己求导计算
import numpy as np
#自己写导数函数
grad_function=lambda x: 2*x - 2
#随机设置极小值初始值
x=0
#迭代次数
epoch=100
#学习率
eta=0.1
#定义列表跟踪梯度下降
x_list=[]
#开始迭代
for i in range(epoch):
#计算导数
grad=grad_function(x)
x -= eta*grad
x_list.append(x)
print(x)
import matplotlib.pyplot as plt
plt.plot(range(epoch),x_list)
plt.show()
0.9999999997962964
2.pytorch实现求导
import torch
#定义一个可训练变量
x=torch.tensor([0.1])
#可求导
x.requires_grad=True
#梯度下降的参数
learning_rate=0.1
epoch=1000
#定义跟踪变量
x_var=[]
for i in range(epoch):
y=x**2 - 2*x + 5
#如果需要计算导数,可以在Tensor上调用.backward(),url:https://blog.csdn.net/weixin_43763731/article/details/88982979
#求导数,retain_grad=True即求导后把图保留
y.backward(retain_graph=True)
#为了防止任何运算都产生图graph
with torch.autograd.no_grad():
#获取求得的导数,用.grad方法。
x -= learning_rate*x.grad
x_var.append(x.detach().clone().numpy())
x.grad.zero_()#一定要置0,第二次重新计算梯度
print(x.detach().clone().numpy())
import matplotlib.pyplot as plt
plt.plot(range(epoch),x_var)
plt.show()
[0.9999999]
例2:使用导数实现线性回归
import matplotlib.pyplot as plt
import numpy as np
import torch
#1.准备数据
age=np.loadtxt("ex2x.dat")
height=np.loadtxt("ex2y.dat")
#数据转换为张量格式
x=torch.from_numpy(np.mat(age).T)#用from_numpy转换为张量
y=torch.tensor(np.mat(height).T)#用tensor转换为张量
#2.训练参数
#超参数
epoch=1000
learning_rate=0.001
#可训练参数
w=torch.tensor([[0.0]],dtype=torch.float64)
b=torch.tensor([[0.0]],dtype=torch.float64)
w.requires_grad=True
b.requires_grad=True
#3.循环迭代梯度更新
list_loss=[]
for i in range(epoch):
#决策输出
y_=x @ w + b # @是内积方式
#选择损失函数,对权重求导
loss=torch.mean((y - y_)**2)
list_loss.append(loss)
#求导数
loss.backward()
#更新权重
#这种是会保留到下次计算中,影响下此计算
# w.data -= learning_rate * w.grad.data
# b.data -= learning_rate * b.grad.data
#这种是不会保留到下次计算中,不影响下此计算
with torch.autograd.no_grad():
w -= learning_rate * w.grad
b -= learning_rate * b.grad
w.grad.zero_()#一定要置0,第二次重新计算梯度
b.grad.zero_()
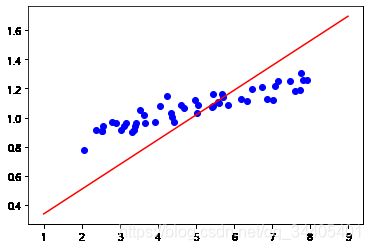
#4.可视化分析训练结果
print(w,b)
x_p=torch.linspace(1,9,100,dtype=torch.float64)#从1到9生成100个数据
y_p=x_p.view(x_p.shape[0],1) @ w +b
plt.scatter(age,height,color=(0,0,1,1))
plt.plot(x_p.detach().numpy(),y_p.detach().numpy(),color=(1,0,0,1))
plt.show()
tensor([[0.1695]], dtype=torch.float64, requires_grad=True) tensor([[0.1698]], dtype=torch.float64, requires_grad=True)
例3:使用导数实现LeNet-5卷积神经网络,完成手写数字识别
import struct
import numpy as np
# 加载图像
def load_image_fromfile(filename):
# 打开文件
with open(filename, 'rb') as fd:
# 循环读取
header_buf = fd.read(16)
# 解析数据
magic_, nums_, w_, h_ = struct.unpack('>iiii', header_buf)
# 保存成ndarray
imgs_ = np.fromfile(fd, dtype=np.uint8)
imgs_ = imgs_.reshape(nums_, h_, w_)
return imgs_
train_x = load_image_fromfile("datasets/train-images.idx3-ubyte")
print(train_x.shape)
(60000, 28, 28)
import matplotlib.pyplot as plt
plt.imshow(train_x[59999], cmap='gray')
plt.show()
import struct
import numpy as np
# 加载图像
def load_label_fromfile(filename):
# 打开文件
with open(filename, 'rb') as fd:
# 循环读取
header_buf = fd.read(8)
# 解析数据
magic_, nums_ = struct.unpack('>ii', header_buf)
# 保存成ndarray
labels_ = np.fromfile(fd, dtype=np.uint8)
return labels_
train_y = load_label_fromfile("datasets/train-labels.idx1-ubyte")
print(train_y[0], train_y[59999])
5 8
5.作业
- 1.使用pytorch实现线性回归
- 2.手写数字读取
5.1 作业1:
import torch
import matplotlib.pyplot as plt
import numpy as np
#加载数据
age=np.loadtxt("ex2x.dat")
height=np.loadtxt("ex2y.dat")
print(age)
print(height)
#将数据处理成每一行代表一个样本
one=np.ones(len(age))
age=np.array(age).reshape(len(age),1)
age=np.column_stack((age,one))
height=np.array(height).reshape(len(height),1)
print(age)
print(height)
#将age变成张量x,height变成张量y
x=torch.tensor(age)
y=torch.tensor(height)
print(x,y)
[2.0658746 2.3684087 2.5399929 2.5420804 2.549079 2.7866882 2.9116825
3.035627 3.1146696 3.1582389 3.3275944 3.3793165 3.4122006 3.4215823
3.5315732 3.6393002 3.6732537 3.9256462 4.0498646 4.2483348 4.3440052
4.3826531 4.4230602 4.6102443 4.6881183 4.9777333 5.0359967 5.0684536
5.4161491 5.4395623 5.4563207 5.5698458 5.6015729 5.6877617 5.7215602
5.8538914 6.1978026 6.3510941 6.4797033 6.7383791 6.8637686 7.0223387
7.0782373 7.1514232 7.4664023 7.5973874 7.7440717 7.7729662 7.8264514
7.9306356]
[0.77918926 0.91596757 0.90538354 0.90566138 0.9389889 0.9668474
0.96436824 0.91445939 0.93933944 0.96074971 0.89837094 0.91209739
0.94238499 0.96624578 1.05265 1.0143791 0.95969426 0.96853716
1.0766065 1.1454978 1.0340625 1.0070009 0.96683648 1.0895919
1.0634462 1.1237239 1.0323374 1.0874452 1.0702988 1.1606493
1.0778037 1.1069758 1.0971875 1.1648603 1.1411796 1.0844156
1.1252493 1.1168341 1.1970789 1.2069462 1.1251046 1.1235672
1.2132829 1.2522652 1.2497065 1.1799706 1.1897299 1.3029934
1.2601134 1.2562267 ]
[[2.0658746 1. ]
[2.3684087 1. ]
[2.5399929 1. ]
[2.5420804 1. ]
[2.549079 1. ]
[2.7866882 1. ]
[2.9116825 1. ]
[3.035627 1. ]
[3.1146696 1. ]
[3.1582389 1. ]
[3.3275944 1. ]
[3.3793165 1. ]
[3.4122006 1. ]
[3.4215823 1. ]
[3.5315732 1. ]
[3.6393002 1. ]
[3.6732537 1. ]
[3.9256462 1. ]
[4.0498646 1. ]
[4.2483348 1. ]
[4.3440052 1. ]
[4.3826531 1. ]
[4.4230602 1. ]
[4.6102443 1. ]
[4.6881183 1. ]
[4.9777333 1. ]
[5.0359967 1. ]
[5.0684536 1. ]
[5.4161491 1. ]
[5.4395623 1. ]
[5.4563207 1. ]
[5.5698458 1. ]
[5.6015729 1. ]
[5.6877617 1. ]
[5.7215602 1. ]
[5.8538914 1. ]
[6.1978026 1. ]
[6.3510941 1. ]
[6.4797033 1. ]
[6.7383791 1. ]
[6.8637686 1. ]
[7.0223387 1. ]
[7.0782373 1. ]
[7.1514232 1. ]
[7.4664023 1. ]
[7.5973874 1. ]
[7.7440717 1. ]
[7.7729662 1. ]
[7.8264514 1. ]
[7.9306356 1. ]]
[[0.77918926]
[0.91596757]
[0.90538354]
[0.90566138]
[0.9389889 ]
[0.9668474 ]
[0.96436824]
[0.91445939]
[0.93933944]
[0.96074971]
[0.89837094]
[0.91209739]
[0.94238499]
[0.96624578]
[1.05265 ]
[1.0143791 ]
[0.95969426]
[0.96853716]
[1.0766065 ]
[1.1454978 ]
[1.0340625 ]
[1.0070009 ]
[0.96683648]
[1.0895919 ]
[1.0634462 ]
[1.1237239 ]
[1.0323374 ]
[1.0874452 ]
[1.0702988 ]
[1.1606493 ]
[1.0778037 ]
[1.1069758 ]
[1.0971875 ]
[1.1648603 ]
[1.1411796 ]
[1.0844156 ]
[1.1252493 ]
[1.1168341 ]
[1.1970789 ]
[1.2069462 ]
[1.1251046 ]
[1.1235672 ]
[1.2132829 ]
[1.2522652 ]
[1.2497065 ]
[1.1799706 ]
[1.1897299 ]
[1.3029934 ]
[1.2601134 ]
[1.2562267 ]]
tensor([[2.0659, 1.0000],
[2.3684, 1.0000],
[2.5400, 1.0000],
[2.5421, 1.0000],
[2.5491, 1.0000],
[2.7867, 1.0000],
[2.9117, 1.0000],
[3.0356, 1.0000],
[3.1147, 1.0000],
[3.1582, 1.0000],
[3.3276, 1.0000],
[3.3793, 1.0000],
[3.4122, 1.0000],
[3.4216, 1.0000],
[3.5316, 1.0000],
[3.6393, 1.0000],
[3.6733, 1.0000],
[3.9256, 1.0000],
[4.0499, 1.0000],
[4.2483, 1.0000],
[4.3440, 1.0000],
[4.3827, 1.0000],
[4.4231, 1.0000],
[4.6102, 1.0000],
[4.6881, 1.0000],
[4.9777, 1.0000],
[5.0360, 1.0000],
[5.0685, 1.0000],
[5.4161, 1.0000],
[5.4396, 1.0000],
[5.4563, 1.0000],
[5.5698, 1.0000],
[5.6016, 1.0000],
[5.6878, 1.0000],
[5.7216, 1.0000],
[5.8539, 1.0000],
[6.1978, 1.0000],
[6.3511, 1.0000],
[6.4797, 1.0000],
[6.7384, 1.0000],
[6.8638, 1.0000],
[7.0223, 1.0000],
[7.0782, 1.0000],
[7.1514, 1.0000],
[7.4664, 1.0000],
[7.5974, 1.0000],
[7.7441, 1.0000],
[7.7730, 1.0000],
[7.8265, 1.0000],
[7.9306, 1.0000]], dtype=torch.float64) tensor([[0.7792],
[0.9160],
[0.9054],
[0.9057],
[0.9390],
[0.9668],
[0.9644],
[0.9145],
[0.9393],
[0.9607],
[0.8984],
[0.9121],
[0.9424],
[0.9662],
[1.0527],
[1.0144],
[0.9597],
[0.9685],
[1.0766],
[1.1455],
[1.0341],
[1.0070],
[0.9668],
[1.0896],
[1.0634],
[1.1237],
[1.0323],
[1.0874],
[1.0703],
[1.1606],
[1.0778],
[1.1070],
[1.0972],
[1.1649],
[1.1412],
[1.0844],
[1.1252],
[1.1168],
[1.1971],
[1.2069],
[1.1251],
[1.1236],
[1.2133],
[1.2523],
[1.2497],
[1.1800],
[1.1897],
[1.3030],
[1.2601],
[1.2562]], dtype=torch.float64)
#定义权重w
w=torch.tensor([[0.0],[0.0]],dtype=torch.float64)
w.requires_grad=True
#定义超参数
times=1000 #训练次数
rate=0.001 #学习率
for i in range(times):
fun_y= x @ w
#定义损失函数
loss=torch.mean((y - fun_y)**2)
#损失函数对w求导
loss.backward()
#更新w
with torch.autograd.no_grad():
w -= w.grad*rate
w.grad.zero_()
#打印w进行查看
print(w)
tensor([[0.1695],
[0.1698]], dtype=torch.float64, requires_grad=True)
#绘制真实数据的散点图和模型的现状图进行对比
pre_y=[]
x=np.loadtxt("ex2x.dat")
y=np.loadtxt("ex2y.dat")
#用 .numpy将tensor转成numpy
w0=w.detach().data[0].numpy()
w1=w.detach().data[1].numpy()
print(w0,w1)
for i in range(len(x)):
pre_y.append(x[i]*w0+w1)
plt.scatter(x,y,color=(0,0,1,1))
plt.plot(x,pre_y,color=(1,0,0,1))
plt.show()
[0.16947101] [0.16979947]
5.2 作业2:
import struct
import numpy as np
import matplotlib.pyplot as plt
#定义一个读取二进制图片的函数
def load_img(name):
#rb:以二进制格式打开一个文件用于只读
with open(name,'rb') as re:
#读取文件头,文件头16个字节,4个整数
header=re.read(16)
#利用struct解析上一步读取的16个字节,解析成魔法字(存放的格式)、图片数量、宽、高四个数字
magic,num,w,h=struct.unpack('>iiii',header)
#读取剩下的图像(图像都用二进制表示)
imgs = np.fromfile(re, dtype=np.uint8)
imgs = imgs.reshape(num, h, w)#转换成矩阵
return imgs
train_x = load_img("datasets/train-images.idx3-ubyte")
plt.imshow(train_x[0], cmap='gray')
plt.show()